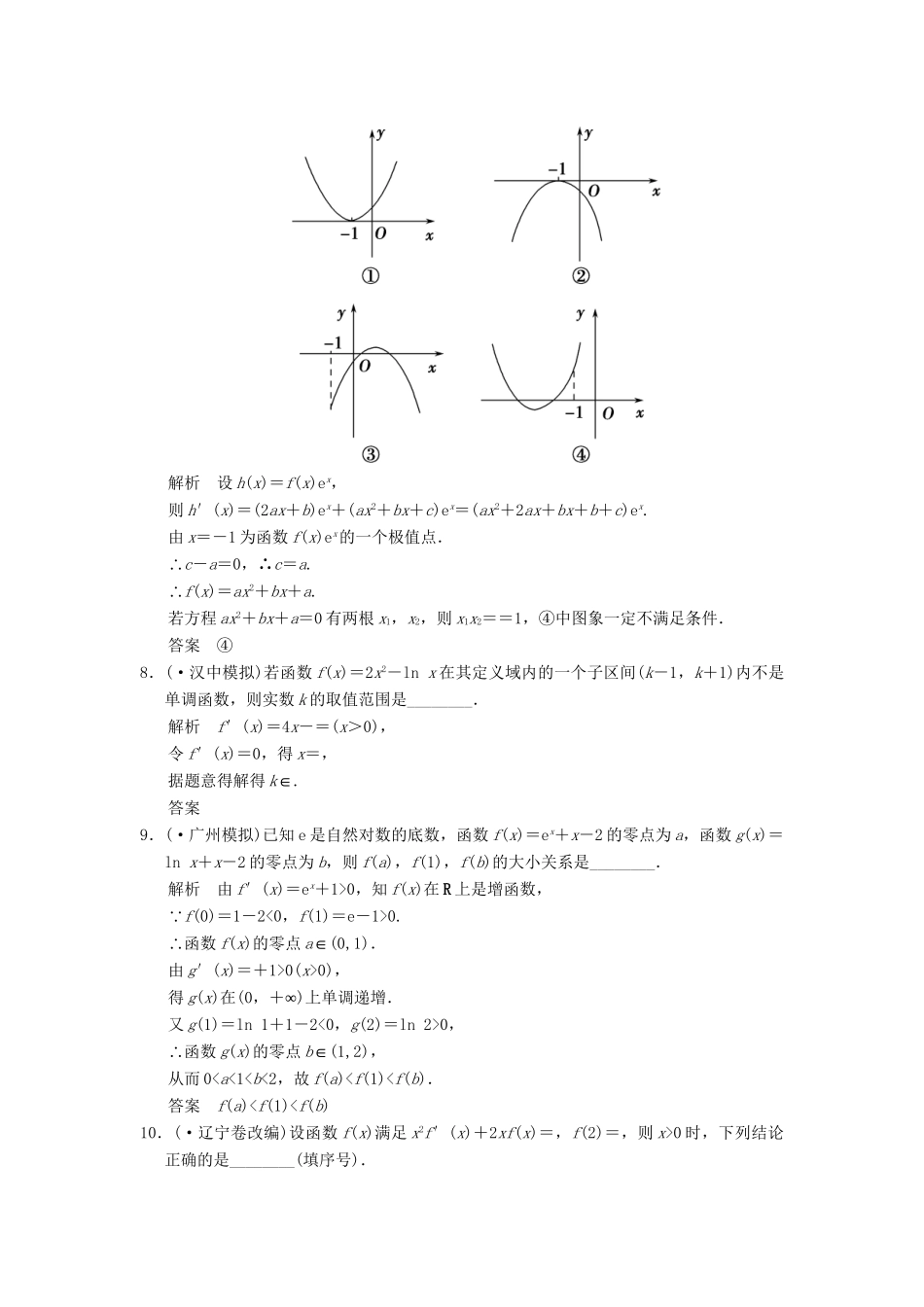
——能力提升练导数及其应用(建议用时:90分钟)一、填空题1.(·襄阳调研)曲线y=x3-2x+4在点(1,3)处的切线的倾斜角为________.解析由y′=3x2-2得y′|x=1=1,即曲线在点(1,3)处的切线斜率为1,所以切线的倾斜角为45°.答案45°2.函数f(x)的定义域为R,f(-1)=2,对任意x∈R,f′(x)>2,则f(x)>2x+4的解集为________.解析设g(x)=f(x)-2x-4,由已知g′(x)=f′(x)-2>0,则g(x)在(∞∞-,+)上递增,又g(-1)=f(-1)-2=0,由g(x)=f(x)-2x-4>0,知x>-1.答案(-1∞,+)3.(·韶关模拟)曲线y=ex在点A处的切线与直线x-y+3=0平行,则点A的坐标为________.解析直线x-y+3=0的斜率为1,所以切线的斜率为1,因为y′=ex,所以由y′=ex=1,解得x=0,此时y=e0=1,即点A的坐标为(0,1).答案(0,1)4.已知函数f(x)=2lnx-xf′(1),则曲线y=f(x)在x=1处的切线方程是________.解析易知f′(x)=-f′(1),令x=1,得f′(1)=2-f′(1),∴f′(1)=1,因此f(x)=2lnx-x,∴f(1)=-1,∴所求的切线方程为y+1=1·(x-1),即x-y-2=0.答案x-y-2=05.(·济南质检)若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于________.解析 f′(x)=12x2-2ax-2b,Δ=4a2+96b>0,又x=1是极值点,∴f′(1)=12-2a-2b=0,即a+b=6,且a>0,b>0,∴ab≤=9,当且仅当a=b“”时=成立,所以ab的最大值为9.答案96.(·青岛模拟)幂指函数y=f(x)g(x)在求导数时,可以运用对数法:在函数解析式两边求对数得lny=g(x)lnf(x),两边求导数得=g′(x)lnf(x)+g(x),于是y′=f(x)g(x)·.运用此法探求y=的单调递增区间为________.解析将函数y=x两边求对数得lny=lnx,两边求导数得=-lnx+·=(1-lnx),所以y′=y·(1-lnx)=·(1-lnx).令y′>0,即1-lnx>0,∴0
0,知f(x)在R上是增函数, f(0)=1-2<0,f(1)=e-1>0.∴函数f(x)的零点a∈(0,1).由g′(x)=+1>0(x>0),得g(x)在(0∞,+)上单调递增.又g(1)=ln1+1-2<0,g(2)=ln2>0,∴函数g(x)的零点b∈(1,2),从而00时,下列结论正确的是________(填序号).①f(x)有极大值,无极小值②f(x)有极小值,无极大值③f(x)既有极大值又有极小值④f(x)既无极大值也无极小值解析由条件,得f′(x)=-=.令g(x)=ex-2x2f(x),则g′(x)=ex-2x2f′(x)-4xf(x)=ex-2(x2f′(x)+2xf(x))=ex-=ex,令g′(x)=0,得x=2.当x>2时,g′(x)>0;当00,∴f(x)在(0∞,+)上单调递增,无极大(小)值.答案④11.若曲线f(x)=ax2+lnx存在垂直于y轴的切线,则实数a的取值范围是________.解析依题意得,f′(x)=2ax+=0(x>0)有实根,所以a=-<0.答案(∞-,0)12.若曲线y=2x-x3在横坐标为-1的点处的切线为l,则点P(3,2)到直线l的距离为________.解析由题意得切点坐标为(-1,-1),切线斜率为k=y′|x=-1=2-3x2|x=-1=2-3×(-1)2=-1.故切线l的方程为y-(-1)=-[x-(-1)],整理得x+y+2=0.∴点P(3,2)到直...