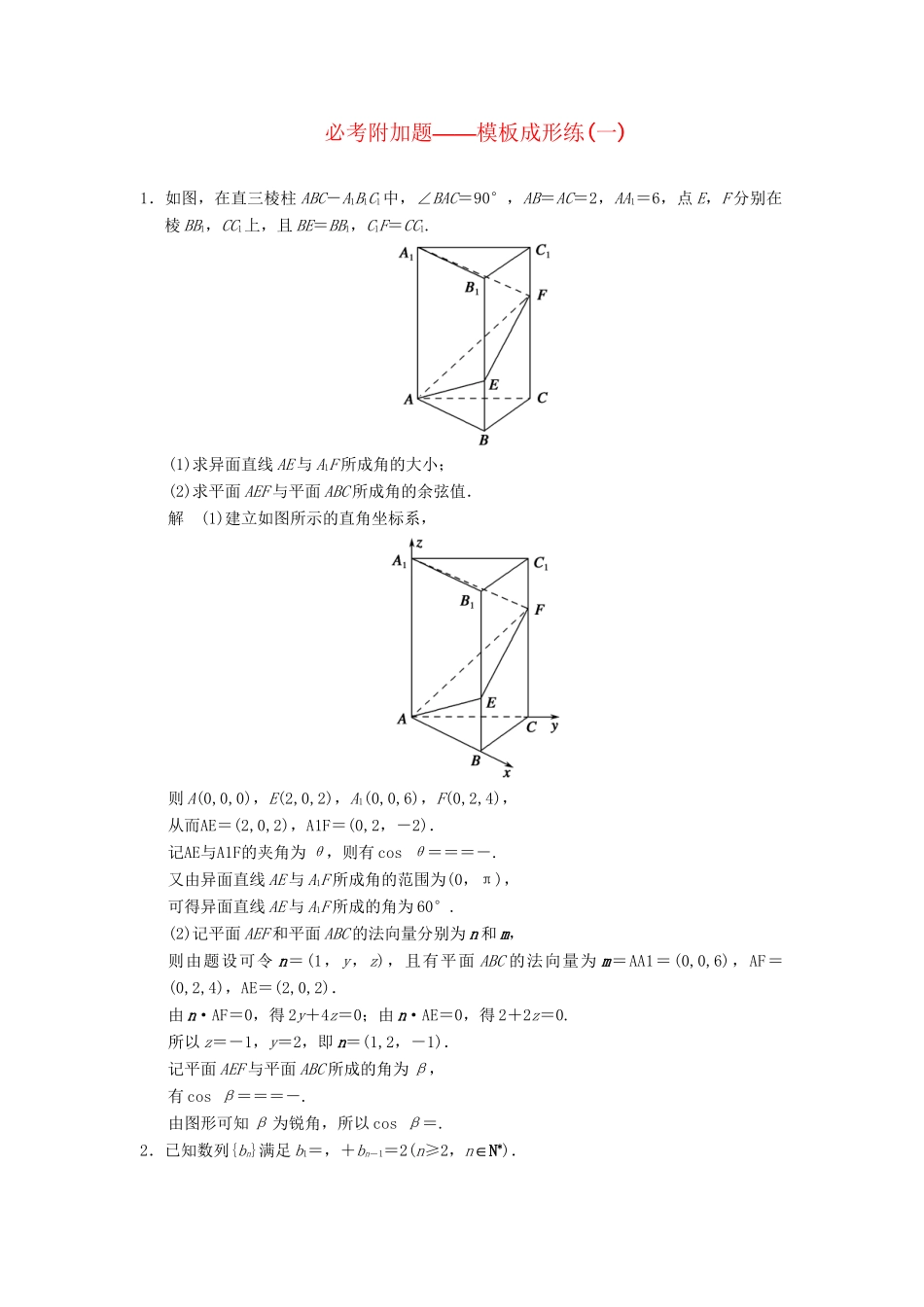
——必考附加题模板成形练(一)1.如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E,F分别在棱BB1,CC1上,且BE=BB1,C1F=CC1.(1)求异面直线AE与A1F所成角的大小;(2)求平面AEF与平面ABC所成角的余弦值.解(1)建立如图所示的直角坐标系,则A(0,0,0),E(2,0,2),A1(0,0,6),F(0,2,4),从而AE=(2,0,2),A1F=(0,2,-2).记AE与A1F的夹角为θ,则有cosθ===-.又由异面直线AE与A1F所成角的范围为(0,π),可得异面直线AE与A1F所成的角为60°.(2)记平面AEF和平面ABC的法向量分别为n和m,则由题设可令n=(1,y,z),且有平面ABC的法向量为m=AA1=(0,0,6),AF=(0,2,4),AE=(2,0,2).由n·AF=0,得2y+4z=0;由n·AE=0,得2+2z=0.所以z=-1,y=2,即n=(1,2,-1).记平面AEF与平面ABC所成的角为β,有cosβ===-.由图形可知β为锐角,所以cosβ=.2.已知数列{bn}满足b1=,+bn-1=2(n≥2,n∈N*).(1)求b2,b3,猜想数列{bn}的通项公式,并用数学归纳法证明;(2)设x=b,y=b,比较xx与yy的大小.解(1)当n=2时,+=2,解得b2=;当n=3时,+=2,解得b3=.猜想bn=.证明:①当n=1时,b1=.②假设当n=k(k∈N*)时,即bk=,则当n=k+1时,+bk=2,即+=2,∴=2-=,bk+1=也成立.由①②得bn=.(2)x=b=n,∴xx=yy.3.三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中,已知AB=2,AC=4,A1A=3.D是BC的中点.(1)求直线DB1与平面A1C1D所成角的正弦值;(2)求二面角B1-A1D-C1的大小的正弦值.解(1)由题意,A(0,0,0),B(2,0,0),C(0,4,0),D(1,2,0),A1(0,0,3),B1(2,0,3),C1(0,4,3).A1D=(1,2,-3),A1C1=(0,4,0).设平面A1C1D的法向量为n=(x,y,z).∵n·A1D=x+2y-3z=0,n·A1C1=4y=0.∴x=3z,y=0.令z=1,得x=3.n=(3,0,1).设直线DB1与平面A1C1D所成角为θ,∵DB1=(1,-2,3),∴sinθ=|cos〈DB1,n〉|==.(2)设平面A1B1D的法向量为m=(a,b,c).A1B1=(2,0,0),∵m·A1D=a+2b-3c=0,m·A1B1=2a=0.∴a=0,2b=3c.令c=2,得b=3.m=(0,3,2).设二面角B1-A1D-C1的大小为α,∴|cosα|=|cos〈m,n〉|===,则sinα==,∴二面角B1-A1D-C1的大小的正弦值为.4.已知整数n≥4,集合M={1,2,3…,,n}的所有3个元素的子集记为A1,A2,…,AC(C∈N*).(1)当n=5时,求集合A1,A2…,,AC中所有元素之和;(2)设mi为Ai中的最小元素,设Pn=m1+m2…++mC,试求Pn(用n表示).解(1)当n=5时,含元素1的子集中,必有除1以外的两个数字,两个数字的选法有C=6个,所以含有数字1的集合有6个.同时含2,3,4,5的子集也各有6个.于是所求元素之和为(1+2+3+4+5)×C=15×6=90.(2)证明不难得到1≤mi≤n-2,mi∈Z,并且以1为最小元素的子集有C个,以2为最小元素的子集有C个,以3为最小元素的子集有C…个,,以n-2为最小元素的子集有C个,则Pn=m1+m2…++mC=1×C+2C+3C…++(n-2)C=(n-2)C+(n-3)C+(n-4)C…++C=C+(n-3)(C+C)+(n-4)C…++C=C+(n-3)(C+C)+(n-4)C…++C=C+(n-3)C+(n-4)C…++C=C+C+(n-4)(C+C)…++C=C+C+(n-4)C…++C=C+C+C…++C=C.