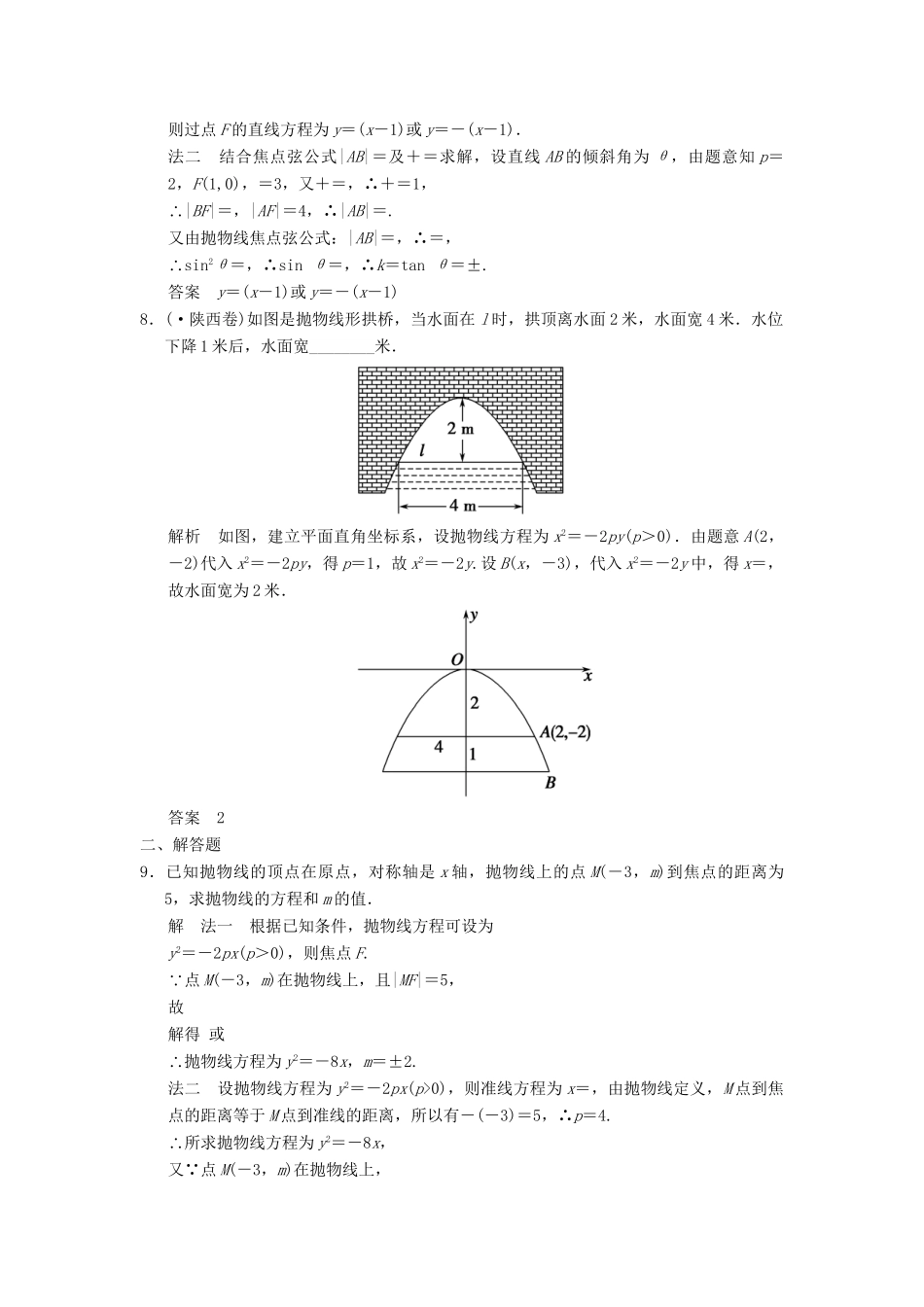
第3讲抛物线基础巩固题组(建议用时:40分钟)一、填空题1.点M(5,3)到抛物线y=ax2的准线的距离为6,那么抛物线的方程是________.解析分两类a>0,a<0可得y=x2,y=-x2.答案y=x2或y=-x22.若点P到直线y=-1的距离比它到点(0,3)的距离小2,则点P的轨迹方程是________.解析由题意可知点P到直线y=-3的距离等于它到点(0,3)的距离,故点P的轨迹是以点(0,3)为焦点,以y=-3为准线的抛物线,且p=6,所以其标准方程为x2=12y.答案x2=12y3.(·济宁模拟)已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则p的值为________.解析圆的标准方程为(x-3)2+y2=16,圆心为(3,0),半径为4.圆心到准线的距离为3-=4,解得p=2.答案24.(·四川卷改编)抛物线y2=8x的焦点到直线x-y=0的距离是________.解析由抛物线方程知2p=8⇒p=4,故焦点F(2,0),由点到直线的距离公式知,F到直线x-y=0的距离d==1.答案15.(·潍坊一模)已知抛物线y2=2px(p>0)的焦点F与双曲线-=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=|AF|,则A点的横坐标为________.解析抛物线的焦点为,准线为x=-.双曲线的右焦点为(3,0),所以=3,即p=6,即y2=12x.过A做准线的垂线,垂足为M,则|AK|=|AF|=|AM|,即|KM|=|AM|,设A(x,y),则y=x+3,代入y2=12x,解得x=3.答案36.已知抛物线y2=4x上一点M与该抛物线的焦点F的距离|MF|=4,则点M的横坐标x0=________.解析抛物线y2=4x的焦点为F(1,0),准线为x=-1.根据抛物线的定义,点M到准线的距离为4,则M的横坐标为3.答案37.(·新课标全国Ⅱ卷改编)设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为________.解析法一由|AF|=3|BF|,得AF=3FB,而F点坐标为(1,0),设B(x0,y0),则从而可解得A的坐标为(4-3x0,-3y0),因为点A,B都在抛物线上,所以解得x0=,y0=±,所以kl==±.则过点F的直线方程为y=(x-1)或y=-(x-1).法二结合焦点弦公式|AB|=及+=求解,设直线AB的倾斜角为θ,由题意知p=2,F(1,0),=3,又+=,∴+=1,∴|BF|=,|AF|=4,∴|AB|=.又由抛物线焦点弦公式:|AB|=,∴=,∴sin2θ=,∴sinθ=,∴k=tanθ=±.答案y=(x-1)或y=-(x-1)8.(·陕西卷)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽________米.解析如图,建立平面直角坐标系,设抛物线方程为x2=-2py(p>0).由题意A(2,-2)代入x2=-2py,得p=1,故x2=-2y.设B(x,-3),代入x2=-2y中,得x=,故水面宽为2米.答案2二、解答题9.已知抛物线的顶点在原点,对称轴是x轴,抛物线上的点M(-3,m)到焦点的距离为5,求抛物线的方程和m的值.解法一根据已知条件,抛物线方程可设为y2=-2px(p>0),则焦点F. 点M(-3,m)在抛物线上,且|MF|=5,故解得或∴抛物线方程为y2=-8x,m=±2.法二设抛物线方程为y2=-2px(p>0),则准线方程为x=,由抛物线定义,M点到焦点的距离等于M点到准线的距离,所以有-(-3)=5,∴p=4.∴所求抛物线方程为y2=-8x,又 点M(-3,m)在抛物线上,故m2=(-8)×(-3),∴m=±2.10.设抛物线C:y2=4x,F为C的焦点,过F的直线l与C相交于A,B两点.(1)设l的斜率为1,求|AB|的大小;(2)求证:OA·OB是一个定值.(1)解 由题意可知抛物线的焦点F为(1,0),准线方程为x=-1,∴直线l的方程为y=x-1,设A(x1,y1),B(x2,y2),由得x2-6x+1=0,∴x1+x2=6,由直线l过焦点,则|AB|=|AF|+|BF|=x1+x2+2=8.(2)证明设直线l的方程为x=ky+1,由得y2-4ky-4=0,∴y=4k+2∴y1+y2=4k,y1y2=-4,OA=(x1,y1),OB=(x2,y2). OA·OB=x1x2+y1y2=(ky1+1)(ky2+1)+y1y2=k2y1y2+k(y1+y2)+1+y1y2=-4k2+4k2+1-4=-3.∴OA·OB是一个定值.能力提升题组(建议用时:25分钟)一、填空题1.已知双曲线C1:-=1(a>0,b>0)的离心率为2.若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为________.解析 -=1的离心率为2,∴=2,即==4,∴=.x2=2py的...