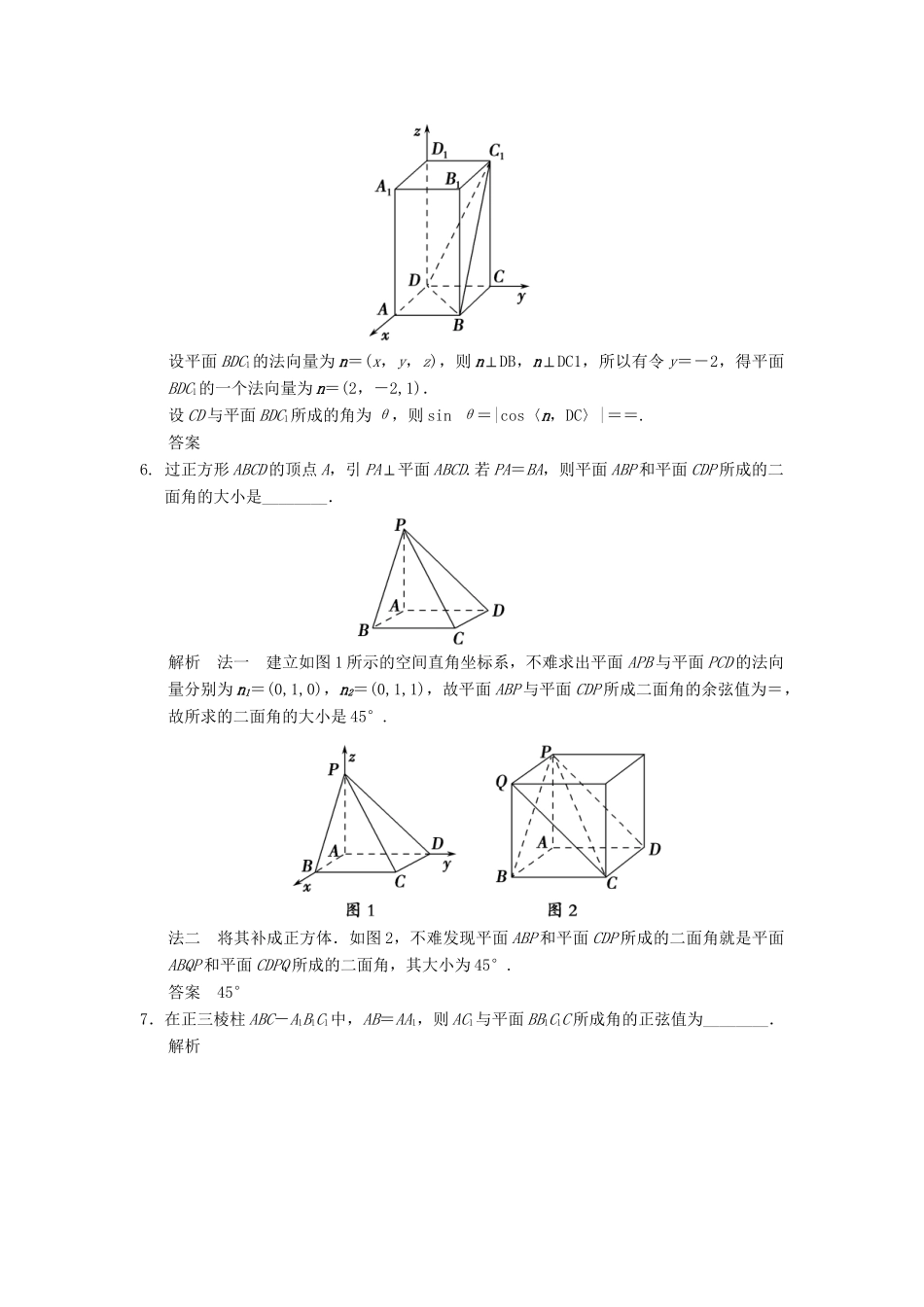
第7讲立体几何中的向量方法(二)——求空间角基础巩固题组(建议用时:40分钟)一、填空题1.平面α的一个法向量为n=(1,-,0),则y轴与平面α所成的角的大小为________.解析y轴的方向向量为m=(0,1,0),设y轴与平面α所成的角为θ,则sinθ=|cos〈m,n〉|, cos〈m,n〉===-,∴sinθ=,∴θ=.答案2.如图,在正方体ABCD-A1B1C1D1中,M,N分别是棱CD,CC1的中点,则异面直线A1M与DN所成的角的大小是________.解析以D为原点,分别以DA,DC,DD1所在直线为坐标轴建立空间直角坐标系,设AB=1,则D(0,0,0),N,M,A1(1,0,1),∴DN=,MA1=,∴DN·MA1=1×0+1×+×1=0,∴DN⊥MA1,∴A1M与DN所成的角的大小是90°.答案90°3.在正方体ABCD-A1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为________.解析以A为原点建系,设棱长为1,则A1(0,0,1),E,D(0,1,0),∴A1D=(0,1,-1),A1E=.设平面A1ED的法向量为n1=(1,y,z),则∴∴n1=(1,2,2), 平面ABCD的一个法向量为n2=(0,0,1),∴cos〈n1,n2〉==,故锐二面角的余弦值为.答案4.正方体ABCD-A1B1C1D1的棱长为a,点M在AC1上且AM=MC1,N为B1B的中点,则|MN|为________.解析以D为原点建立如图所示的空间直角坐标系Dxyz,则A(a,0,0),C1(0,a,a),N.设M(x,y,z), 点M在AC1上且AM=MC1,∴(x-a,y,z)=(-x,a-y,a-z)∴x=a,y=,z=.得M,∴|MN|==a.答案a5.在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于________.解析以D为坐标原点,建立空间直角坐标系,如图,设AA1=2AB=2,则D(0,0,0),C(0,1,0),B(1,1,0),C1(0,1,2),则DC=(0,1,0),DB=(1,1,0),DC1=(0,1,2).设平面BDC1的法向量为n=(x,y,z),则n⊥DB,n⊥DC1,所以有令y=-2,得平面BDC1的一个法向量为n=(2,-2,1).设CD与平面BDC1所成的角为θ,则sinθ=|cos〈n,DC〉|==.答案6.过正方形ABCD的顶点A,引PA⊥平面ABCD.若PA=BA,则平面ABP和平面CDP所成的二面角的大小是________.解析法一建立如图1所示的空间直角坐标系,不难求出平面APB与平面PCD的法向量分别为n1=(0,1,0),n2=(0,1,1),故平面ABP与平面CDP所成二面角的余弦值为=,故所求的二面角的大小是45°.法二将其补成正方体.如图2,不难发现平面ABP和平面CDP所成的二面角就是平面ABQP和平面CDPQ所成的二面角,其大小为45°.答案45°7.在正三棱柱ABC-A1B1C1中,AB=AA1,则AC1与平面BB1C1C所成角的正弦值为________.解析建立如图所示的空间直角坐标系,设AB=2,则C1(,1,0),A(0,0,2),AC1=(,1,-2),平面BB1C1C的一个法向量为n=(1,0,0).所以AC1与平面BB1C1C所成角的正弦值为==.答案8.已知O点为空间直角坐标系的原点,向量OA=(1,2,3),OB=(2,1,2),OP=(1,1,2),且点Q在直线OP上运动,当QA·QB取得最小值时,OQ的坐标是________.解析 点Q在直线OP上,∴设点Q(λ,λ,2λ),则QA=(1-λ,2-λ,3-2λ),QB=(2-λ,1-λ,2-2λ),QA·QB=(1-λ)(2-λ)+(2-λ)(1-λ)+(3-2λ)(2-2λ)=6λ2-16λ+10=62-.当λ=时,QA·QB取得最小值-.此时OQ=.答案二、解答题9.(·江苏卷)如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.(1)求异面直线A1B与C1D所成角的余弦值;(2)求平面ADC1与平面ABA1所成二面角的正弦值.解(1)以A为坐标原点,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(2,0,0),C(0,2,0),D(1,1,0),A1(0,0,4),C1(0,2,4),所以A1B=(2,0,-4),C1D=(1,-1,-4).因为cos〈A1B,C1D〉===,所以异面直线A1B与C1D所成角的余弦值为.(2)设平面ADC1的法向量为n1=(x,y,z),因为AD=(1,1,0),AC1=(0,2,4),所以n1·AD=0,n1·AC1=0,即x+y=0且y+2z=0.取z=1,得x=2,y=-2,所以,n1=(2,-2,1)是平面ADC1的一个法向量.取平面AA1B的一个法向量为n2=(0,1,0),设平面ADC1与平面ABA1所成二面角的大小为θ.由|cosθ|===,得sinθ=.因此,平面ADC1与平面ABA1所成二面角的正弦值为.10.(·广州质检)如图所示,在四棱...