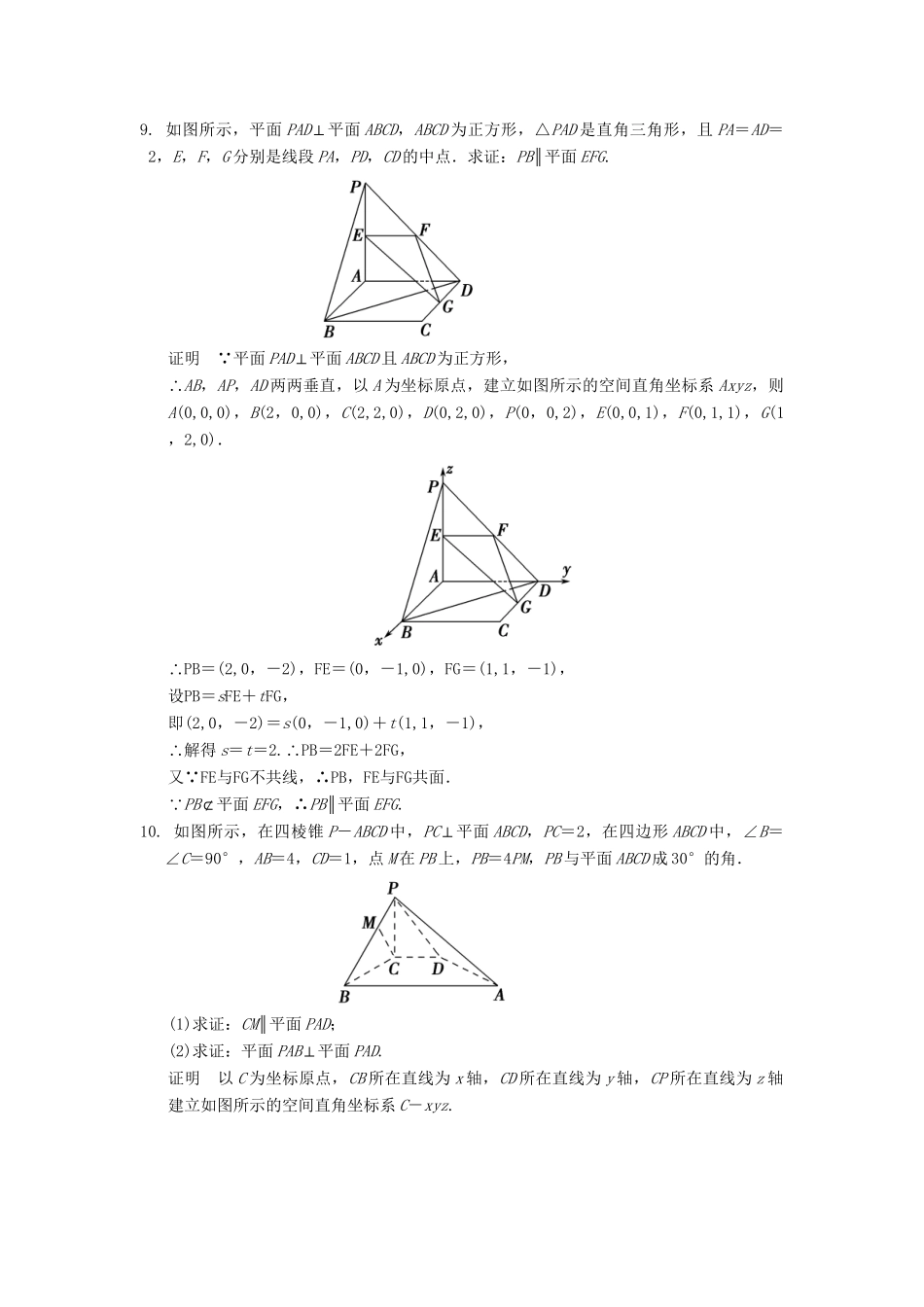
第6讲立体几何中的向量方法(一)——证明平行与垂直基础巩固题组(建议用时:40分钟)一、填空题1.(·徐州模拟)已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).若|a|=,且a分别与AB,AC垂直,则向量a为________.解析由条件知AB=(-2,-1,3),AC=(1,-3,2),设a=(x,y,z)则有解可得a=±(1,1,1).答案(1,1,1)或(-1,-1,-1)2.若AB=λCD+μCE,则直线AB与平面CDE的位置关系是________.解析 AB=λCD+μCE,∴AB,CD,CE共面.则AB与平面CDE的位置关系是平行或在平面内.答案平行或在平面内3.设a=(1,2,0),b=(1,0,1)“,则c”“=是c⊥a,c⊥b且c”为单位向量的________条件.解析当c=时,c⊥a,c⊥b且c为单位向量,反之则不成立.答案充分不必要4.如图,在长方体ABCD-A1B1C1D1中,AB=2,AA1=,AD=2,P为C1D1的中点,M为BC的中点.则AM与PM的位置关系为________(“”“”“”填平行、垂直、异面).解析以D点为原点,分别以DA,DC,DD1所在直线为x,y,z轴,建立如图所示的空间直角坐标系D-xyz,依题意,可得,D(0,0,0),P(0,1,),C(0,2,0),A(2,0,0),M(,2,0).∴PM=(,2,0)-(0,1,)=(,1,-),AM=(,2,0)-(2,0,0)=(-,2,0),∴PM·AM=(,1,-)·(-,2,0)=0,即PM⊥AM,∴AM⊥PM.答案垂直5.如图,正方形ABCD与矩形ACEF所在平面互相垂直,AB=,AF=1,M在EF上,且AM∥平面BDE.则M点的坐标为________.解析连接OE,由AM∥平面BDE,且AM⊂平面ACEF,平面ACEF∩平面BDE=OE,∴AM∥EO,又O是正方形ABCD对角线交点,∴M为线段EF的中点.在空间坐标系中,E(0,0,1),F(,,1).由中点坐标公式,知点M的坐标.答案6.已知平面α和平面β的法向量分别为a=(1,1,2),b=(x,-2,3),且α⊥β,则x=________.解析 α⊥β,∴a·b=x-2+6=0,则x=-4.答案-47.已知平面α内的三点A(0,0,1),B(0,1,0),C(1,0,0),平面β的一个法向量n=(-1,-1,-1).则不重合的两个平面α与β的位置关系是________.解析AB=(0,1,-1),AC=(1,0,-1),∴n·AB=0,n·AC=0,∴n⊥AB,n⊥AC,故n也是α的一个法向量.又 α与β不重合,∴α∥β.答案平行8.已知点P是平行四边形ABCD所在的平面外一点,如果AB=(2,-1,-4),AD=(4,2,0),AP=(-1,2,-1).对于结论:①AP⊥AB;②AP⊥AD;③AP是平面ABCD的法向量;④AP∥BD.其中正确的是________.解析 AB·AP=0,AD·AP=0,∴AB⊥AP,AD⊥AP,则①②正确.又AB与AD不平行,∴AP是平面ABCD的法向量,则③正确.由于BD=AD-AB=(2,3,4),AP=(-1,2,-1),∴BD与AP不平行,故④错误.答案①②③二、解答题9.如图所示,平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=AD=2,E,F,G分别是线段PA,PD,CD的中点.求证:PB∥平面EFG.证明 平面PAD⊥平面ABCD且ABCD为正方形,∴AB,AP,AD两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系Axyz,则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0).∴PB=(2,0,-2),FE=(0,-1,0),FG=(1,1,-1),设PB=sFE+tFG,即(2,0,-2)=s(0,-1,0)+t(1,1,-1),∴解得s=t=2.∴PB=2FE+2FG,又 FE与FG不共线,∴PB,FE与FG共面. PB⊄平面EFG,∴PB∥平面EFG.10.如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.(1)求证:CM∥平面PAD;(2)求证:平面PAB⊥平面PAD.证明以C为坐标原点,CB所在直线为x轴,CD所在直线为y轴,CP所在直线为z轴建立如图所示的空间直角坐标系C-xyz. PC⊥平面ABCD,∴∠PBC为PB与平面ABCD所成的角,∴∠PBC=30°. PC=2,∴BC=2,PB=4.∴D(0,1,0),B(2,0,0),A(2,4,0),P(0,0,2),M,∴DP=(0,-1,2),DA=(2,3,0),CM=,(1)设n=(x,y,z)为平面PAD的一个法向量,则即∴令y=2,得n=(-,2,1). n·CM=-×+2×0+1×=0,∴n⊥CM,又CM⊄平面PAD,∴CM∥平面PAD.(2)取AP的中点E,并连接BE,则E(,2,1),BE=(-,2,1), PB=AB,∴BE⊥PA.又...