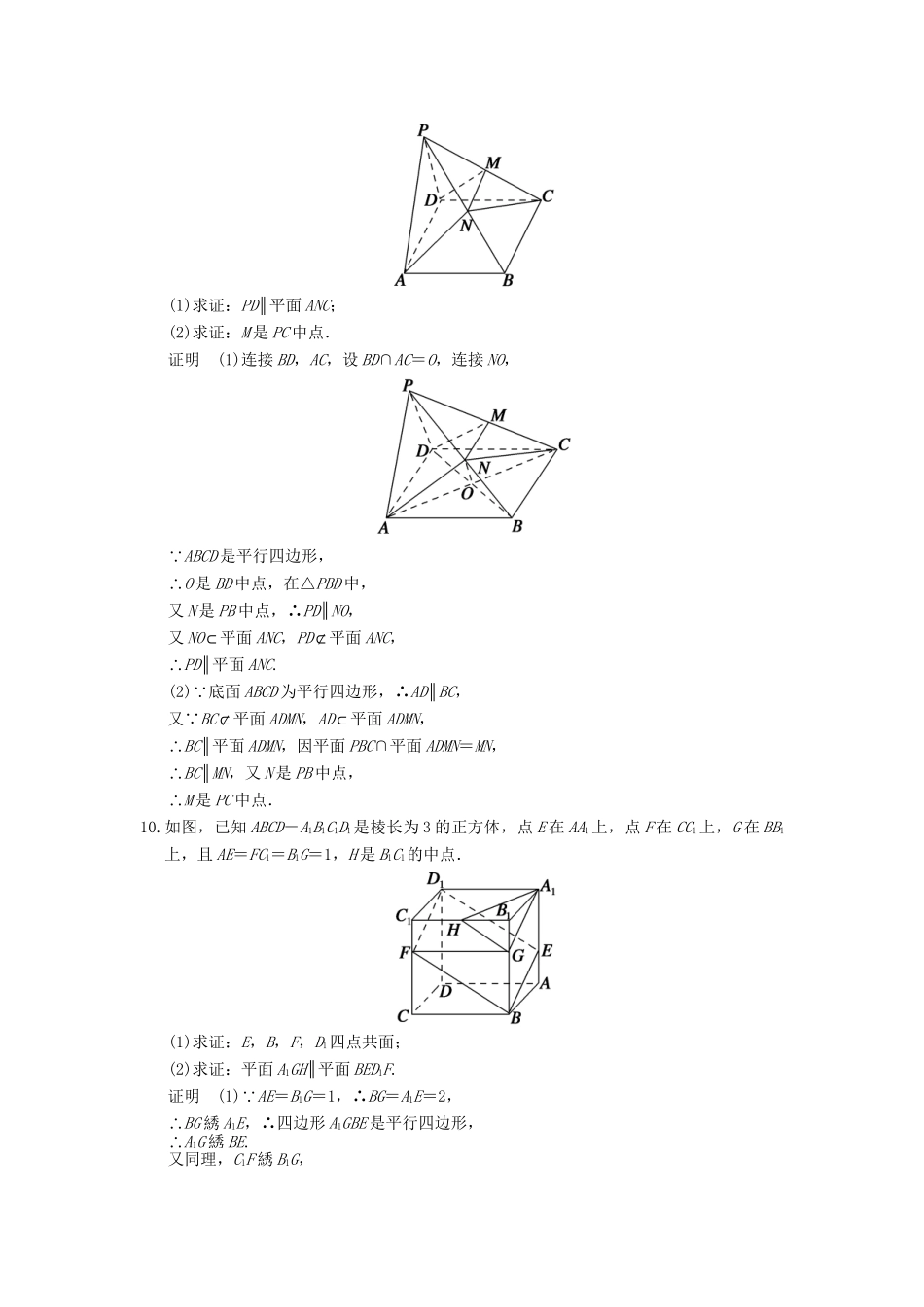
第3讲直线、平面平行的判定与性质基础巩固题组(建议用时:40分钟)一、填空题1.已知直线a,b,c及平面α,β,则①a∥α,b⊂α;②a∥α,b∥α;③a∥c,b∥c;④a∥α,α∩β=b条件中,能使a∥b成立的是________.解析由平行公理知③正确,①中a与b可能平行或异面.②中a,b可能平行或相交或异面,④中a,b可能平行或异面.答案③2.在梯形ABCD中,AB∥CD,AB⊂平面α,CD⊄平面α,则直线CD与平面α内的直线的位置关系是________.解析 AB∥CD,AB⊂α,CD⊄α⇒CD∥α,∴CD和平面α内的直线没有公共点.答案平行或异面3.平面α∥平面β,点A,C∈α,B,D∈β,则直线AC∥直线BD的充要条件是________.①AB∥CD;②AD∥CB;③AB与CD相交;④A,B,C,D四点共面.解析充分性:A,B,C,D四点共面,由平面与平面平行的性质知AC∥BD.必要性显然成立.答案④4.(·汕头质检)若m,n为两条不重合的直线,α,β为两个不重合的平面,给出以下四个结论:①若m,n都平行于平面α,则m,n一定不是相交直线②若m,n都垂直于平面α,则m,n一定是平行直线③已知α,β互相平行,m,n互相平行,若m∥α,则n∥β④若m,n在平面α内的射影互相平行,则m,n互相平行其中正确结论的序号是________.解析①中,m,n可为相交直线;②正确;③中,n可以平行β,也可以在β内;④中,m,n也可能异面.答案②5.在空间四边形ABCD中,E,F分别为AB,AD上的点,且AE∶EB=AF∶FD=1∶4,又H,G分别为BC,CD的中点,则EF与平面BCD的关系为________;四边形EFGH的形状是________.解析如图,由题意知EF∥BD,且EF=BD.HG∥BD,且HG=BD.∴EF∥HG,且EF≠HG.∴四边形EFGH是梯形.又EF⊄平面BCD,HG⊂平面BCD.∴EF∥平面BCD.答案平行,梯形6.过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有________条.解析过三棱柱ABC-A1B1C1的任意两条棱的中点作直线,记AC,BC,A1C1,B1C1的中点分别为E,F,E1,F1,则直线EF,E1F1,EE1,FF1,E1F,EF1均与平面ABB1A1平行,故符合题意的直线共6条.答案67.(·衡阳质检)在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.解析如图.连接AC,BD交于O点,连接OE,因为OE∥BD1,而OE⊂平面ACE,BD1⊄平面ACE,所以BD1∥平面ACE.答案平行8.(·金丽衢十二校联考)设α,β,γ是三个平面,a,b是两条不同直线,有下列三个条件:①a∥γ,b⊂β;②a∥γ,b∥β;③b∥β,a⊂γ.“如果命题α∩β=a,b⊂γ,且________,则a∥b”为真命题,则可以在横线处填入的条件是________(把所有正确的题号填上).解析由面面平行的性质定理可知,①正确;当b∥β,a⊂γ时,a和b在同一平面内,且没有公共点,所以平行,③正确.故应填入的条件为①或③.答案①或③二、解答题9.(·徐州一模)四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB中点,过A,N,D三点的平面交PC于M.(1)求证:PD∥平面ANC;(2)求证:M是PC中点.证明(1)连接BD,AC,设BD∩AC=O,连接NO, ABCD是平行四边形,∴O是BD中点,在△PBD中,又N是PB中点,∴PD∥NO,又NO⊂平面ANC,PD⊄平面ANC,∴PD∥平面ANC.(2) 底面ABCD为平行四边形,∴AD∥BC,又 BC⊄平面ADMN,AD⊂平面ADMN,∴BC∥平面ADMN,因平面PBC∩平面ADMN=MN,∴BC∥MN,又N是PB中点,∴M是PC中点.10.如图,已知ABCD-A1B1C1D1是棱长为3的正方体,点E在AA1上,点F在CC1上,G在BB1上,且AE=FC1=B1G=1,H是B1C1的中点.(1)求证:E,B,F,D1四点共面;(2)求证:平面A1GH∥平面BED1F.证明(1) AE=B1G=1,∴BG=A1E=2,∴BG綉A1E,∴四边形A1GBE是平行四边形,∴A1G綉BE.又同理,C1F綉B1G,∴四边形C1FGB1是平行四边形,∴FG綉C1B1綉D1A1,∴四边形A1GFD1是平行四边形.∴A1G綉D1F,∴D1F綉EB,故E、B、F、D1四点共面.(2) H是B1C1的中点,∴B1H=.又B1G=1,∴=.又=,且∠FCB=∠GB1H=90°,∴△B1HG∽△CBF,∴∠B1GH=∠CFB=∠FBG,∴HG∥FB.又由(1)知A1G∥BE,且HG∩A1G=G,FB∩BE=B,∴平面A1GH∥平面BED1F.能力提升题组(建议用时:25分钟)一、填空题1.如图,两...