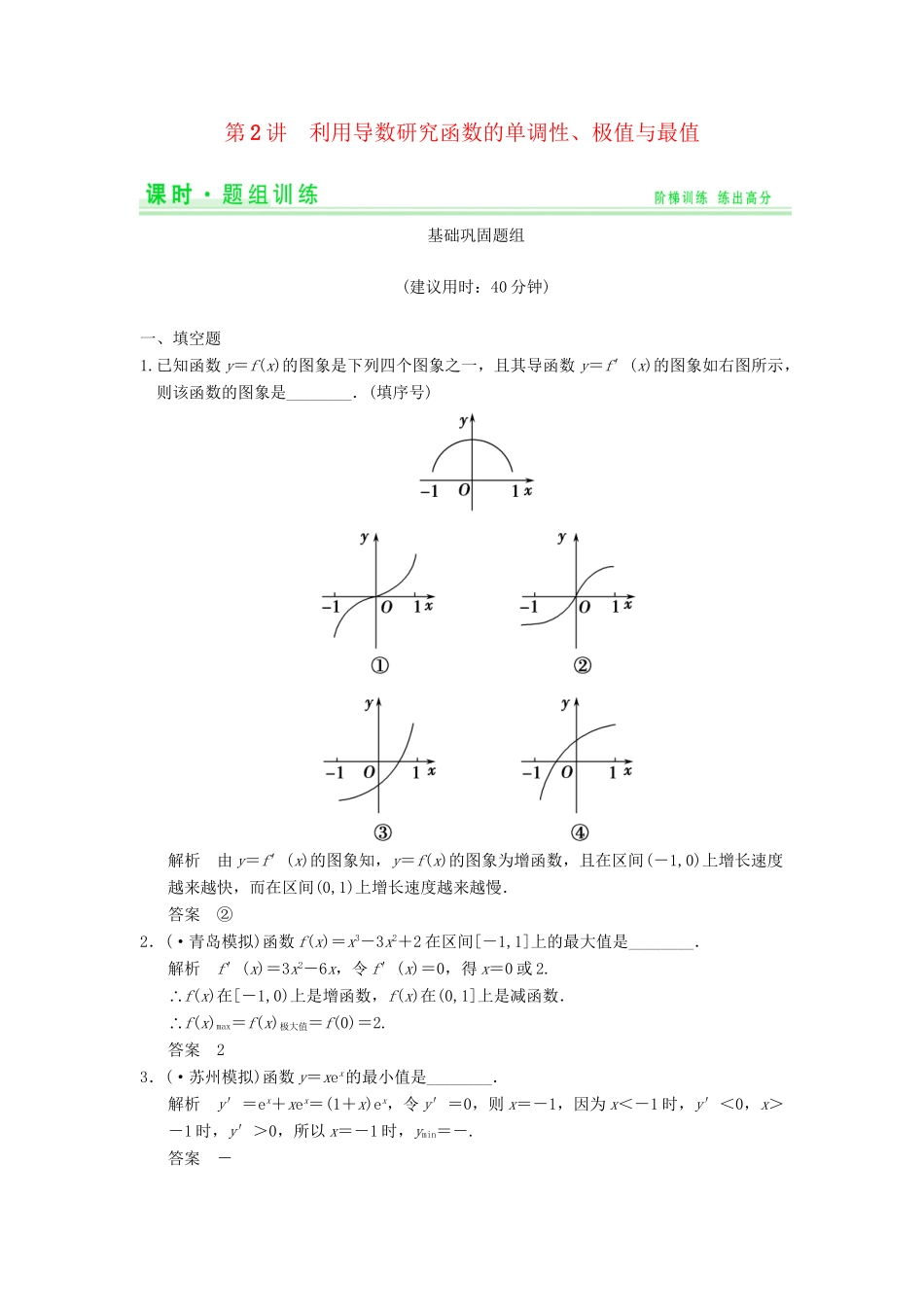
第2讲利用导数研究函数的单调性、极值与最值基础巩固题组(建议用时:40分钟)一、填空题1.已知函数y=f(x)的图象是下列四个图象之一,且其导函数y=f′(x)的图象如右图所示,则该函数的图象是________.(填序号)解析由y=f′(x)的图象知,y=f(x)的图象为增函数,且在区间(-1,0)上增长速度越来越快,而在区间(0,1)上增长速度越来越慢.答案②2.(·青岛模拟)函数f(x)=x3-3x2+2在区间[-1,1]上的最大值是________.解析f′(x)=3x2-6x,令f′(x)=0,得x=0或2.∴f(x)在[-1,0)上是增函数,f(x)在(0,1]上是减函数.∴f(x)max=f(x)极大值=f(0)=2.答案23.(·苏州模拟)函数y=xex的最小值是________.解析y′=ex+xex=(1+x)ex,令y′=0,则x=-1,因为x<-1时,y′<0,x>-1时,y′>0,所以x=-1时,ymin=-.答案-4.(·威海期末考试)函数y=lnx-x2的极值点为________.解析函数的定义域为(0∞,+),函数的导数为y′=-2x=,令y′==0,解得x=,当x>时,y′<0,当0<x<时,y′>0,所以当x=时,函数取得极大值,故函数的极值点为.答案5.(·福建卷改编)设函数f(x)的定义域为R,x0(x0≠0)是f(x)的极大值点,以下结论一定正确的是________(填序号).①∀x∈R,f(x)≤f(x0)②-x0是f(-x)的极小值点③-x0是-f(x)的极小值点④-x0是-f(-x)的极小值点解析①错,因为极大值未必是最大值;②错,因为函数y=f(x)与函数y=f(-x)的图象关于y轴对称,-x0应是f(-x)的极大值点;③错,函数y=f(x)与函数y=-f(x)的图象关于x轴对称,x0应为-f(x)的极小值点;④正确,函数y=f(x)与y=-f(-x)的图象关于原点对称,-x0应为y=-f(-x)的极小值点.答案④6.若函数f(x)=在x=1处取极值,则a=________.解析由f′(x)===0,∴x2+2x-a=0,x≠-1,又f(x)在x=1处取极值,∴x=1是x2+2x-a=0的根,∴a=3.答案37.函数f(x)=的单调递减区间是________.解析f′(x)=,令f′(x)<0得lnx-1<0,且lnx≠0.∴00),f′(x)=x-5+=.令f′(x)=0,解得x=2或3.当03时,f′(x)>0,故f(x)在(0,2),(3∞,+)上为增函数;当20,所以g(x)在(1∞,+)上为增...