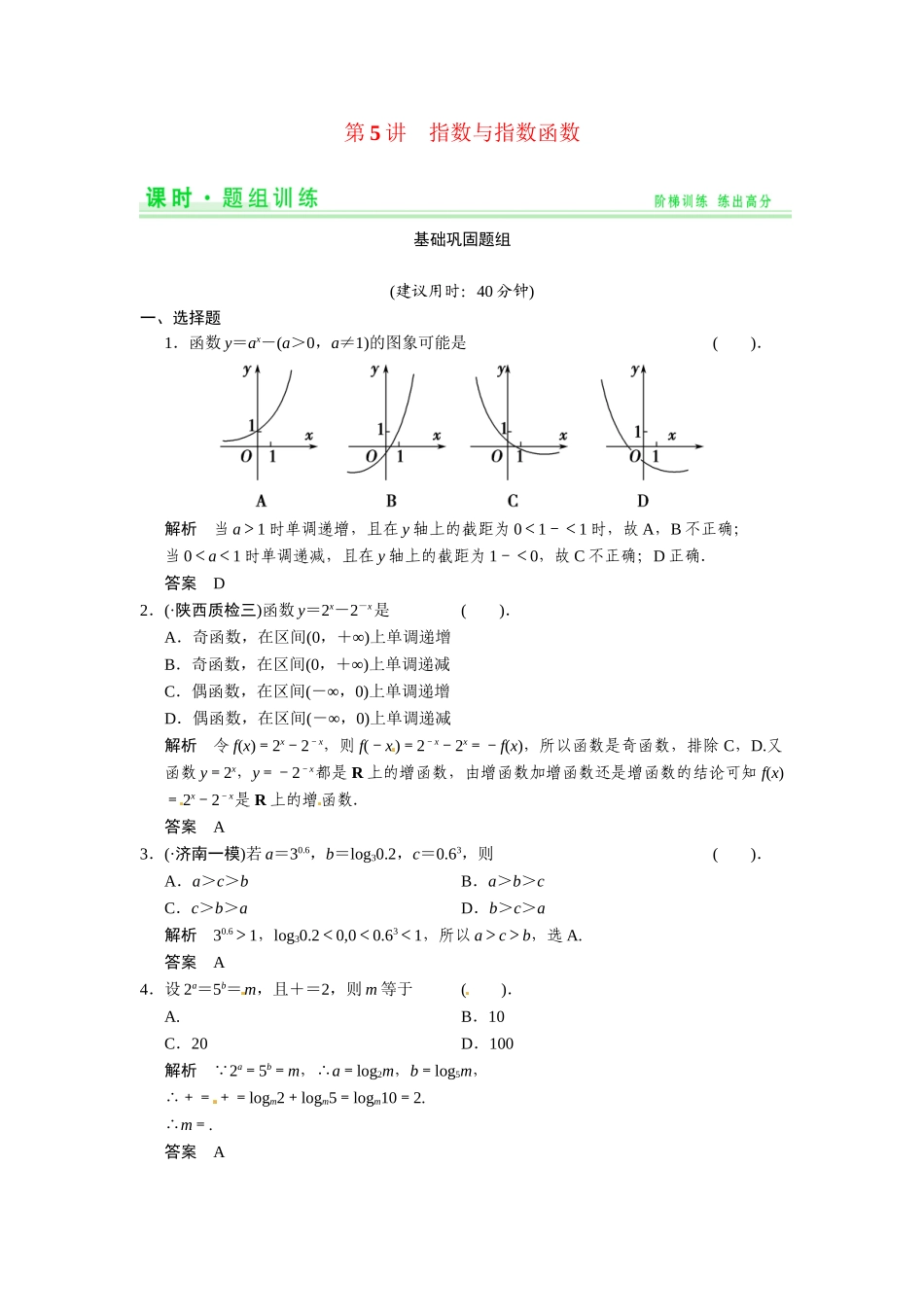
第5讲指数与指数函数基础巩固题组(建议用时:40分钟)一、选择题1.函数y=ax-(a>0,a≠1)的图象可能是().解析当a>1时单调递增,且在y轴上的截距为0<1-<1时,故A,B不正确;当0<a<1时单调递减,且在y轴上的截距为1-<0,故C不正确;D正确.答案D2.(·陕西质检三)函数y=2x-2-x是().A.奇函数,在区间(0,+∞)上单调递增B.奇函数,在区间(0,+∞)上单调递减C.偶函数,在区间(-∞,0)上单调递增D.偶函数,在区间(-∞,0)上单调递减解析令f(x)=2x-2-x,则f(-x)=2-x-2x=-f(x),所以函数是奇函数,排除C,D.又函数y=2x,y=-2-x都是R上的增函数,由增函数加增函数还是增函数的结论可知f(x)=2x-2-x是R上的增函数.答案A3.(·济南一模)若a=30.6,b=log30.2,c=0.63,则().A.a>c>bB.a>b>cC.c>b>aD.b>c>a解析30.6>1,log30.2<0,0<0.63<1,所以a>c>b,选A.答案A4.设2a=5b=m,且+=2,则m等于().A.B.10C.20D.100解析∵2a=5b=m,∴a=log2m,b=log5m,∴+=+=logm2+logm5=logm10=2.∴m=.答案A5.函数y=ax-b(a>0且a≠1)的图象经过第二、三、四象限,则ab的取值范围为().A.(1,+∞)B.(0,+∞)C.(0,1)D.无法确定解析函数经过第二、三、四象限,所以函数单调递减且图象与y轴的交点在负半轴上.而当x=0时,y=a0-b=1-b,由题意得解得所以ab∈(0,1).答案C二、填空题6.(a>0)的值是________.7.(·盐城模拟)已知函数f(x)=a-x(a>0,且a≠1),且f(-2)>f(-3),则a的取值范围是________.解析因为f(x)=a-x=x,且f(-2)>f(-3),所以函数f(x)在定义域上单调递增,所以>1,解得0<a<1.答案(0,1)8.函数f(x)=ax(a>0,a≠1)在[1,2]中的最大值比最小值大,则a的值为________.解析当0<a<1时,a-a2=,∴a=或a=0(舍去).当a>1时,a2-a=,∴a=或a=0(舍去).综上所述,a=或.答案或三、解答题9.设f(x)=+是定义在R上的函数.(1)f(x)可能是奇函数吗?(2)若f(x)是偶函数,求a的值.解(1)假设f(x)是奇函数,由于定义域为R,∴f(-x)=-f(x),即+=-,整理得(ex+e-x)=0,即a+=0,即a2+1=0,显然无解.∴f(x)不可能是奇函数.(2)因为f(x)是偶函数,所以f(-x)=f(x),即+=+,整理得(ex-e-x)=0,又∵对任意x∈R都成立,∴有a-=0,得a=±1.10.设a>0且a≠1,函数y=a2x+2ax-1在[-1,1]上的最大值是14,求a的值.解令t=ax(a>0且a≠1),则原函数化为y=(t+1)2-2(t>0).①当0<a<1时,x∈[-1,1],t=ax∈,此时f(t)在上为增函数.所以f(t)max=f=2-2=14.所以2=16,所以a=-或a=.又因为a>0,所以a=.②当a>1时,x∈[-1,1],t=ax∈,此时f(t)在上是增函数.所以f(t)max=f(a)=(a+1)2-2=14,解得a=3(a=-5舍去).综上得a=或3.能力提升题组(建议用时:25分钟)一、选择题1.(·惠州质检)设f(x)=|3x-1|,c<b<a且f(c)>f(a)>f(b),则下列关系式中一定成立的是().A.3c>3bB.3b>3aC.3c+3a>2D.3c+3a<2解析作f(x)=|3x-1|的图象如图所示,由图可知,要使c<b<a且f(c)>f(a)>f(b)成立,则有c<0且a>0,∴3c<1<3a,∴f(c)=1-3c,f(a)=3a-1,又f(c)>f(a),∴1-3c>3a-1,即3a+3c<2,故选D.答案D2.(·杭州质检)已知函数f(x)=是定义域上的递减函数,则实数a的取值范围是().A.B.C.D.解析∵函数f(x)=是定义域上的递减函数,∴即解得