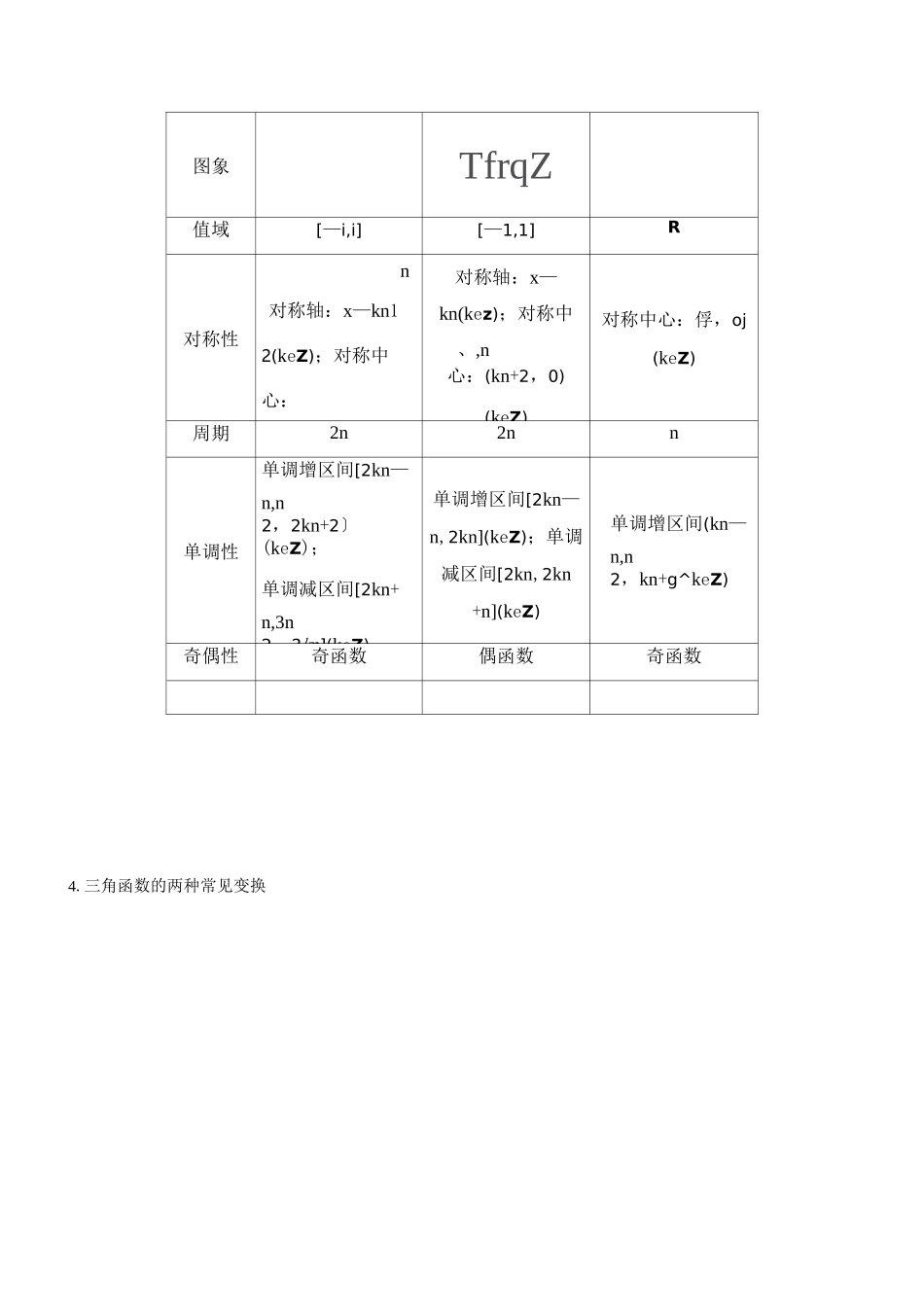
知识回顾理清教材n正弦函数y=sinx,x$[0,2n啲图象中,五个关键点是:(0,0),(㊁,1),(n,0),3n(亍-授课主题三角函数的图像与性质复习教学目的三角函数的图象和性质的考查中,以图象的变换,函数的单调性、奇偶性、周期性、对称性、最值等作为热点内容,并且往往与三角变换公式相互联系,有时也与平面向量,解三角形或不等式内容相互交汇教学重点运用三角函数知识解决综合问题教学内容基础知识・自主学习I要点梳理1.用五点法作正弦函数和余弦函数的简图(2n,0).2、三角函数定义、同角关系与诱导公式(1)定义:设a是一个任意角,它的终边与单位圆交于点P(x,y),则sina=y,cosa=x,tana=".各象限x角的三角函数值的符号:一全正,二正弦,三正切,四余弦.(2)同角关系:sin2a+cos2a=1,Sina=tana.cosa(3)诱导公式:在kn+a,kwz的诱导公式中“奇变偶不变,符号看象限”.3.正弦函数、余弦函数、正切函数的图象和性质函数性质y=sinxy=cosxy=tanx定义域RRn{xlxHkn12,keZ}图象TfrqZ值域[—i,i][—1,1]R对称性n对称轴:x—kn12(keZ);对称中心:对称轴:x—kn(kez);对称中、,n心:(kn+2,0)(keZ)对称中心:俘,oj(keZ)周期2n2nn单调性单调增区间[2kn—n,n2,2kn+2〕(keZ);单调减区间[2kn+n,3n2,2kn](keZ)单调增区间[2kn—n,2kn](keZ);单调减区间[2kn,2kn+n](keZ)单调增区间(kn—n,n2,kn+g^keZ)奇偶性奇函数偶函数奇函数4.三角函数的两种常见变换⑵了=sin丄横坐标变为原来的丄倍纵坐标不变・向左(乎>0)或向右(产"西了7个单位'横坐标变为原来的丄倍I3严——応茶莎—z,、纵坐标变为原来的血倍严叔讣卄)—扇耘―"$=Asin(ewl-甲)(一4>0’*Q"0)-^向左(^0)或向右(p<0)2)J—siniDje;*■平移|卫|个单位3f,、纵坐标变为原来的A倍严沁s+回—扇冠―'JJ=Asin(田工+
Q,题型分类・深度剖析题型一求三角函数的定义域和最值(nxnA【例1(1)(2012.山东)函数y=2sin(_6—3,(0WxW9)的最大值与最小值之和为()A.2—\:3B.0C.—1D.—1—弋3(2)函数y=t~~1—1的定义域为.tanx1解析(1)利用三角函数的性质先求出函数的最值.,,n,nnIn:°0WxW9,・・—3*6"—3*~6,n3E[—AJ3,2],・・y+y.=2—百.maxminnx^4+kn,kezkez.sinx>0,即1J2kn0,解析(1)要使函数有意义必须有[1cosx—j±0.n・••函数的定义域为{xl2kn