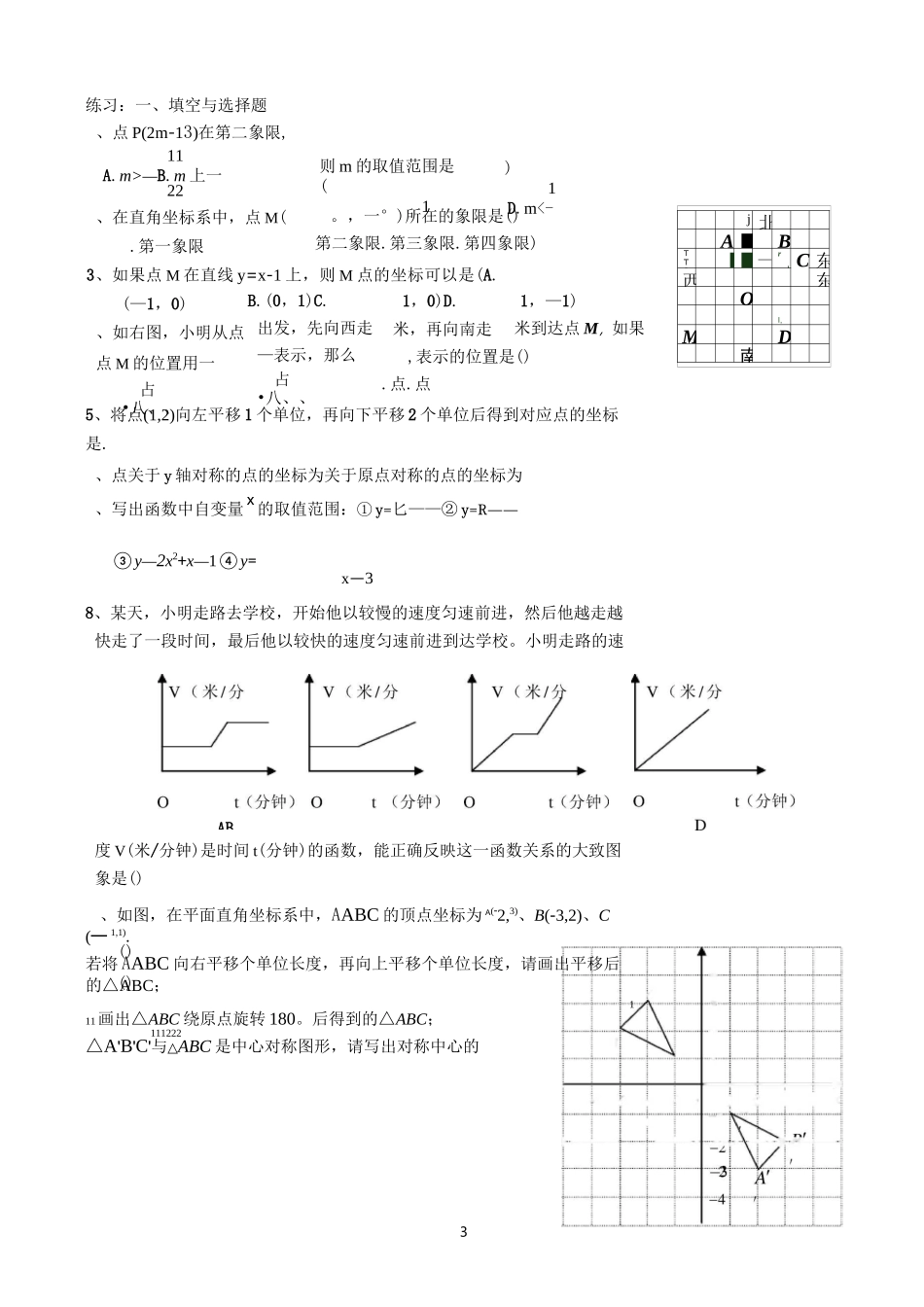
1例((函数》《函数基础知识》一、平面直角坐标系、具有公共原点的两条互相垂直的数轴构成平面直角坐标系;、有序数对准确地确定平面内点的位置;、象限(注:坐标轴不属于任何象限)、点M(a、b)关于x轴的对称点的坐标是(a、一b);关于轴的对称点的坐标是(一a、b);关于原点的对称点的坐标是(一a、一b)二、函数、概念:一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个值,y都有唯一的值与其对应,那么y是x的函数,x是自变量;、函数的表示法:解析法、列表法、图象法(画函数图象的方法:列表、描点、连线);、自变量的取值范围:整式(一般为全体实数)、分式(使分母不为的实数)、二次根式(使被开方数为非负数的实数)、分式与二次根式的综合。例、()已知在平面直角坐标系中有一点P(m—,m+),若点P在x轴上,则m=;若点P在第二象限,则m的取值范围是()已知平面直角坐标系中两点A(x、1),B(—、y)①若点A、B关于x轴对称,则x=,,=;②若点A、B关于y轴对称,则x=,,=③若点A、B关于原点对称,则x=,y=;()足球守门员大脚开出去的球的髙度随时间的变化而变化,这一过程可近似地用右边那幅图刻画()、写出以下函数中自变量x的取值范围:①y=2x②y=J3-x1x+1④y=刃⑤歹二、口+丄—x—2x—3、如图,在平面直角坐标系xoy中,A(-l,5),B(一1,0),C(一4,3).、求出AABC的面积.)在图中作出AABC关于y轴的对称图形AABC,111A,B,C的坐标.111()在图中作出△ABC关于原点逆时针旋转的AABC,222出点A、B、C的坐标.八y第二象限第一象限(―,+)(+,+)O,x第三象限第四象限(+,—)学道教育初中数学23则m的取值范围是(1C.m<—)1D.m<-()()练习:一、填空与选择题、点P(2m-13)在第二象限,11A.m>—B.m上一225、将点(1,2)向左平移1个单位,再向下平移2个单位后得到对应点的坐标是.、点关于y轴对称的点的坐标为关于原点对称的点的坐标为、写出函数中自变量x的取值范围:①y=匕——②y=R——③y—2x2+x—1④y=x—38、某天,小明走路去学校,开始他以较慢的速度匀速前进,然后他越走越快走了一段时间,最后他以较快的速度匀速前进到达学校。小明走路的速度V(米/分钟)是时间t(分钟)的函数,能正确反映这一函数关系的大致图象是()、如图,在平面直角坐标系中,AABC的顶点坐标为A(-2,3)、B(-3,2)、C(一1,1).若将AABC向右平移个单位长度,再向上平移个单位长度,请画出平移后的△ABC;111画出△ABC绕原点旋转180。后得到的△ABC;111222△A'B'C'与△ABC是中心对称图形,请写出对称中心的AB。,一°)所在的象限是()第二象限.第三象限.第四象限)、在直角坐标系中,点M(.第一象限3、如果点M在直线y=x-1上,则M点的坐标可以是(A.(—1,0)、如右图,小明从点点M的位置用一占•八、、B.(0,1)C.出发,先向西走—表示,那么占•八、、1,0)D.米,再向南走1,—1)米到达点M,如果,表示的位置是().点.点j北A■BTT?■■—1rJC东西东OI,MD南学道教育初中数学4■——::►—4—3—2—1O1C234x1■C-2—1j«■ij...••>S";"…①……?坐标:;()顺次连结C、C、C'、C,所得到的图形是轴对称图形12吗?15与y轴的交点坐标为(,b),如下图:③k<0,b>0④k<0,b<0直线y=kix+bi与直线y=k2X+b2相互:平行(ki=j垂直(kl-k2一次函数》、一次函数的概念:、一次函数:y=kx+b(k丰0)正比例函数:y=kx(k丰0)、一次函数的图象是一条直线(正比例函数的图象一定经过原点)、一次函数y=kx+b(kM)的图象是直线,其性质为:、当k>时,y随x的增大而增大;当kV,y随x的增大而减小;即“k"的值决定直线的方向,"b”的值决定直线与y轴的交点坐标;、直线y=kx+b与x轴的交点坐标为(—-,0),k①k>0,b>0®k>0,b<0三、直线y=kx+b的平移、平行、垂直、平移:左“+”右“一”,上“+”下“一”;例、()在平面直角坐标系中,函数y=—x+1的图象经过().一、二、三象限.二、三、四象限.一、三、四象限.一、二、四象限()一次函数y=kx+b与y=x+a的图象如图,则下列结论:①k<0;12②a>0;y=x+a③当x<3时,y