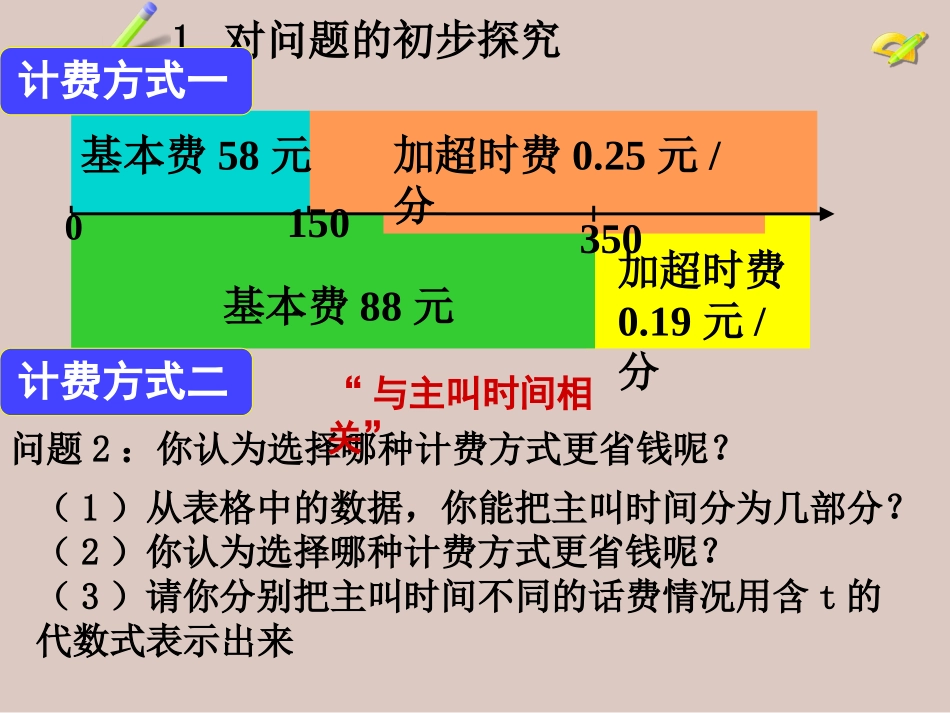
一元一次方程的应用------方案选择问题1.对问题的初步探究问题1:下表给出的是两种移动电话的计费方式:免费0.1935088方式二免费0.2515058方式一被叫主叫超时费(元/分)主叫限定时间(分)月使用费(元)你了解表格中这些数字的含义吗?探究3问题2:你认为选择哪种计费方式更省钱呢?“与主叫时间相关”1.对问题的初步探究加超时费0.19元/分基本费88元加超时费0.25元/分基本费58元3500150计费方式一计费方式二(1)从表格中的数据,你能把主叫时间分为几部分?(2)你认为选择哪种计费方式更省钱呢?(3)请你分别把主叫时间不同的话费情况用含t的代数式表示出来一、自主学习一、自主学习设一个月内用移动电话主叫为t分(t是正整数).根据表1,当t在不同时间范围内取值,列表说明按方式一和方式二如何计费.主叫时间t/分方式一计费/元方式二计费/元t<150t=15015035058+0.25(t-150)58+0.25(350-150)=10858+0.25(t-150)88+0.19(t-350)585888888888主叫时间t/分方式一计费/元方式二计费/元t小于1505888t等于1505888t大于150且小于35058+0.25(t-150)88t等于35010888t大于35058+0.25(t-150)88+0.19(t-350)划算划算划算二、合作探究二、合作探究(4)在两种收费方式下,会不会有这么一个时间,打同样多时间的电话,却收费相同呢?(5)如果有这一时间,在哪段时间?如何根据收费相等列出方程?主叫时间t/分方式一计费/元方式二计费/元t大于150且小于35058+0.25(t-150)88依题意得:58+0.25(t-150)=88去括号得:58+0.25t-37.5=88移项、合并同类项得:0.25t=67.5系数化1得:t=270∴当t=270分时,两种计费方式的费用相等,那么当150350分时,两种计费方式哪种更合算呢?当t>350分时,可以看出,按方式一的计费为108元加上超出350分的部分的超时费0.25(t-350),按方式二的计费为88元加上超时费0.19(t-350),故按方式二的计费少.(6):综合以上的分析,可以发现:时,选择方式一省钱;时,选择方式二省钱.0计费方式一计费方式二270t小于270分t大于270分二、合作探究二、合作探究◆计费方案选择问题:1、分段计费问题,需要分类讨论,弄清如何分类。2、在分类讨论的某个范围内,可借助字母表达式表示计费。3、不同方案的选择的转折点可通过方程计算寻找。◆计费方案选择问题:1、分段计费问题,需要分类讨论,弄清如何分类。2、在分类讨论的某个范围内,可借助字母表达式表示计费。3、不同方案的选择的转折点可通过方程计算寻找。三、方法归纳三、方法归纳例2.某牛奶加工厂现有鲜奶9吨.若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润2000元.该工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片每天可加工1吨.受人员限制,两种加工方式不可同时进行.受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕.为此,该厂设计了两种可行方案:方案一:尽可能多的制成奶片,其余直接销售鲜牛奶;方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成.你认为选择哪种方案获利最多,为什么?例3.校长带领学校的市级三好生去北京旅游.甲旅行社说:“如果校长买全票一张,其他学生享半价优惠。”乙旅行社说:“包括校长在内,全部6折优惠。”全票价为100元.(1)设学生人数为x人,那么这两家旅行社的总费用分别为多少?(2)当学生人数为多少时,两家费用一样多?如何选择旅行社更划算?四、概括整合四、概括整合解决优化方案问题的一般步骤:1、运用一元一次方程解应用题的方法求解两种方案值相等的情况;2、用特殊值试探法选择方案,取小于(或大于)一元一次方程解的值,分别代入两种方案中计算,比较两种方案的优劣后下结论.请回顾电话计费问题的...