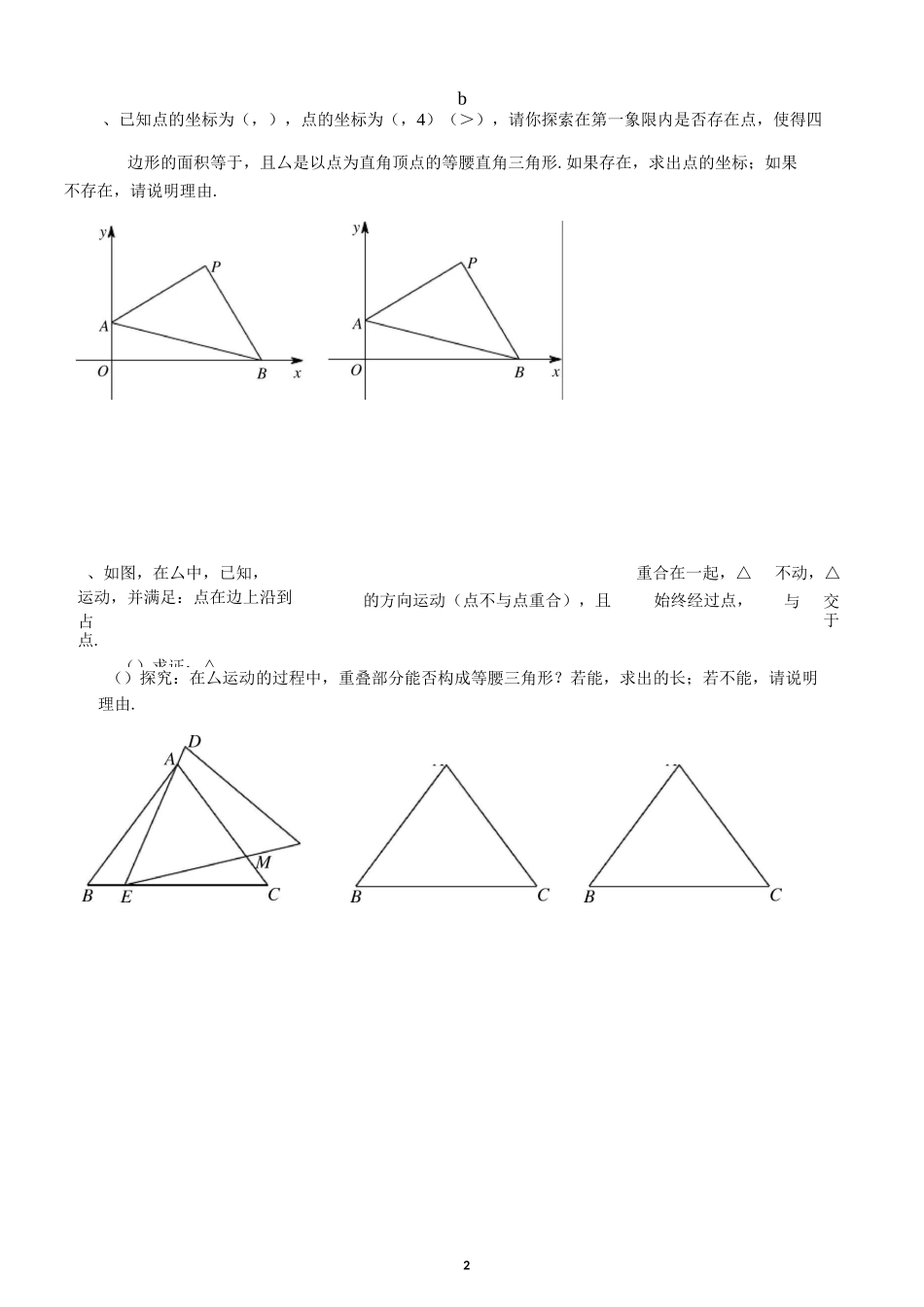
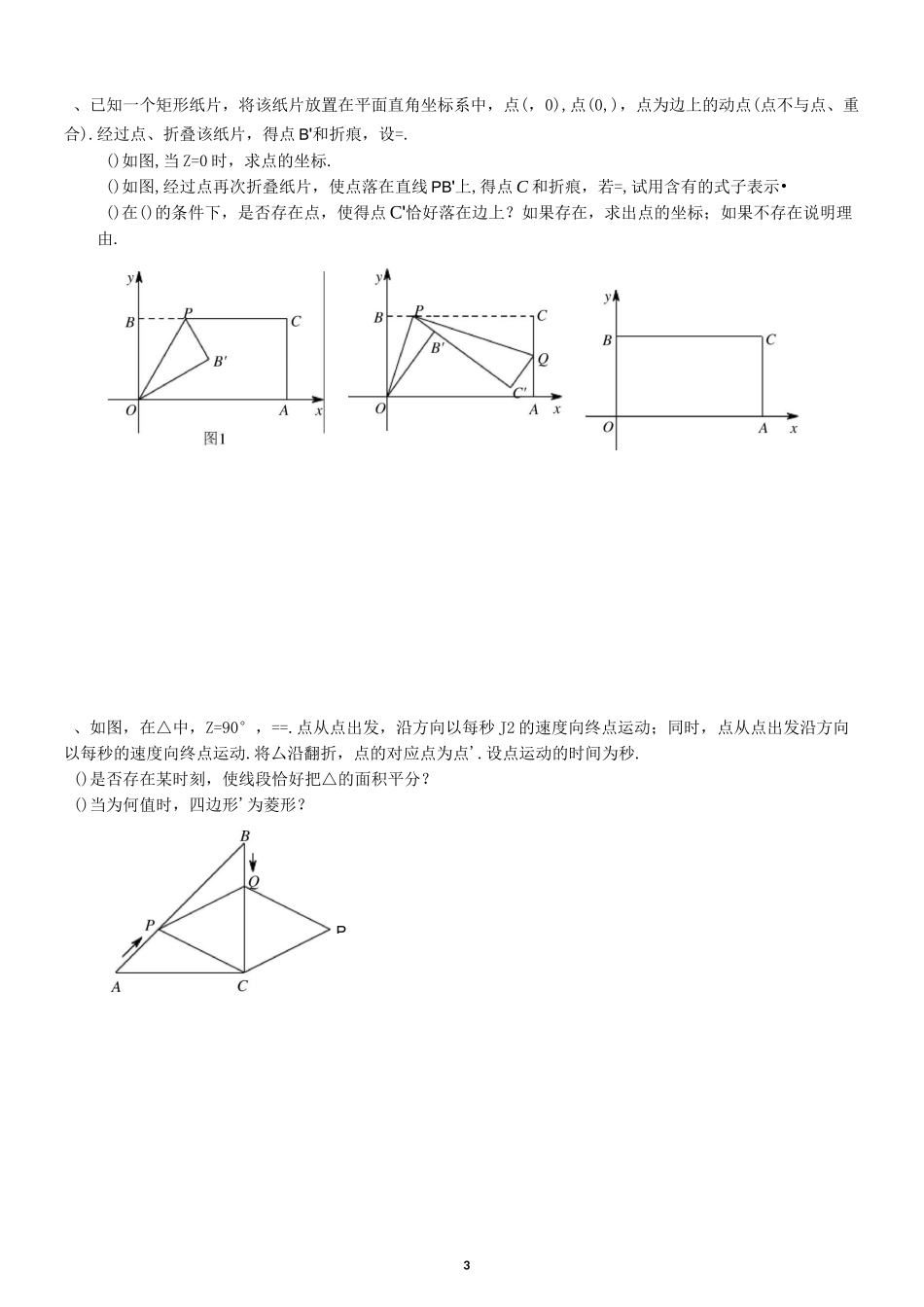
1存在性问题一、知识点睛存在性问题:通常是在变化的过程中,根据已知条件,探索某种状态是否存在的题目.常以动点、图形运动、几何变换、函数为背景出题.解决存在性问题的思考方向:1.分析特殊状态的形成因素,常由和共同组成;2.把和结合起来,挖掘几何特征、表达,建等式求解.二、精讲精练、如图,已知△中,,,.如果点由出发沿方向向点匀速运动,同时点由出发沿方向向点匀速运动,它们的速度均为.连接,设运动的时间为(单位:)(<<).解答下列问题:()当为何值时,〃?()是否存在某时刻,使线段恰好把△的面积平分?若存在,求出此时的值;若不存在,请说明理由.()如图,把厶沿翻折,得到四边形'.那么是否存在某时刻,使四边形'为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.、如图,在平面直角坐标系中,四边形是梯形,〃,点的坐标为,,点的坐标为,,点在轴的正半轴上.动点在上运动,从点出发到点;动点在上运动,从点出发到点.两个动点同时出发,速度都是每秒个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为秒.()求线段的长;当为何值时,〃?()连接,那么是否存在这样的,使与互相垂直?若存在,求出这时的值;若不存在,请说明理由.图图2b、已知点的坐标为(,),点的坐标为(,4)(>),请你探索在第一象限内是否存在点,使得四边形的面积等于,且厶是以点为直角顶点的等腰直角三角形.如果存在,求出点的坐标;如果不存在,请说明理由.、如图,在厶中,已知,重合在一起,△不动,△运动,并满足:点在边上沿到占的方向运动(点不与点重合),且始终经过点,与交于点.()求证:△.()探究:在厶运动的过程中,重叠部分能否构成等腰三角形?若能,求出的长;若不能,请说明理由.3、已知一个矩形纸片,将该纸片放置在平面直角坐标系中,点(,0),点(0,),点为边上的动点(点不与点、重合).经过点、折叠该纸片,得点B'和折痕,设=.()如图,当Z=0时,求点的坐标.()如图,经过点再次折叠纸片,使点落在直线PB'上,得点C和折痕,若=,试用含有的式子表示•()在()的条件下,是否存在点,使得点C'恰好落在边上?如果存在,求出点的坐标;如果不存在说明理由.、如图,在△中,Z=90°,==.点从点出发,沿方向以每秒J2的速度向终点运动;同时,点从点出发沿方向以每秒的速度向终点运动.将厶沿翻折,点的对应点为点'.设点运动的时间为秒.()是否存在某时刻,使线段恰好把△的面积平分?()当为何值时,四边形'为菱形?P4、如图,在平面直角坐标系中,矩形的顶点的坐标是(0,),现有两动点,,点从点出发沿线段(不包括端点、)以每秒个单位长度的速度匀速向点运动,点从点出发沿线段(不包括端点、)以每秒个单位长度的速度匀速向点运动.点,同时出发,同时停止.设运动的时间为(秒),当二(秒)时,=2^5.()求点的坐标,并直接写出的取值范围.()连接并延长交轴于点,把沿翻折交延长线于点.为何值时,四边形是梯形?y*、已知:如图,在△中,Z=90°,=,=.点由出发沿方向向点匀速运动,速度为;点由出发沿方向向点匀速运动,速度为.连接,若设运动的时间为()(0VV),解答下列问题:()当为何值时,〃?()设厶的面积为(),求与之间的函数关系式.()是否存在某一时刻,使线段恰好把△的周长和面积同时平分?若存在,求出此时的值;若不存在,说明理由.()如图,连接,并把△沿翻折,得到四边形PQP'C,那么是否存在某一时刻,使四边形PQP'C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.P'5、在矩形中,,是上的一个动点(不与、()求证:••,分別以,所在直线为轴和轴,建立如图所示的平面直角坐标系.k重合),过点的反比例函数y=_(k>0)的图象与边交于点.x()是否存在这样的点,使得将△沿对折后,点恰好落在上?若存在,求出此时的长;、如图,在△中,==,丄于点,且=.点从点出发,沿方向匀速运动,速度为;同时直线由点出发,沿方向匀速运动,速度为,运动过程中始终保持〃,直线交于点、交于点、交于点.连接,设运动时间为vv.()当为何值时,四边形是平行四边形?()设四边形的面积为,求与之间的函数关系式.()是否存...