江西高中数学立体几何初步72棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积导学案VIP免费

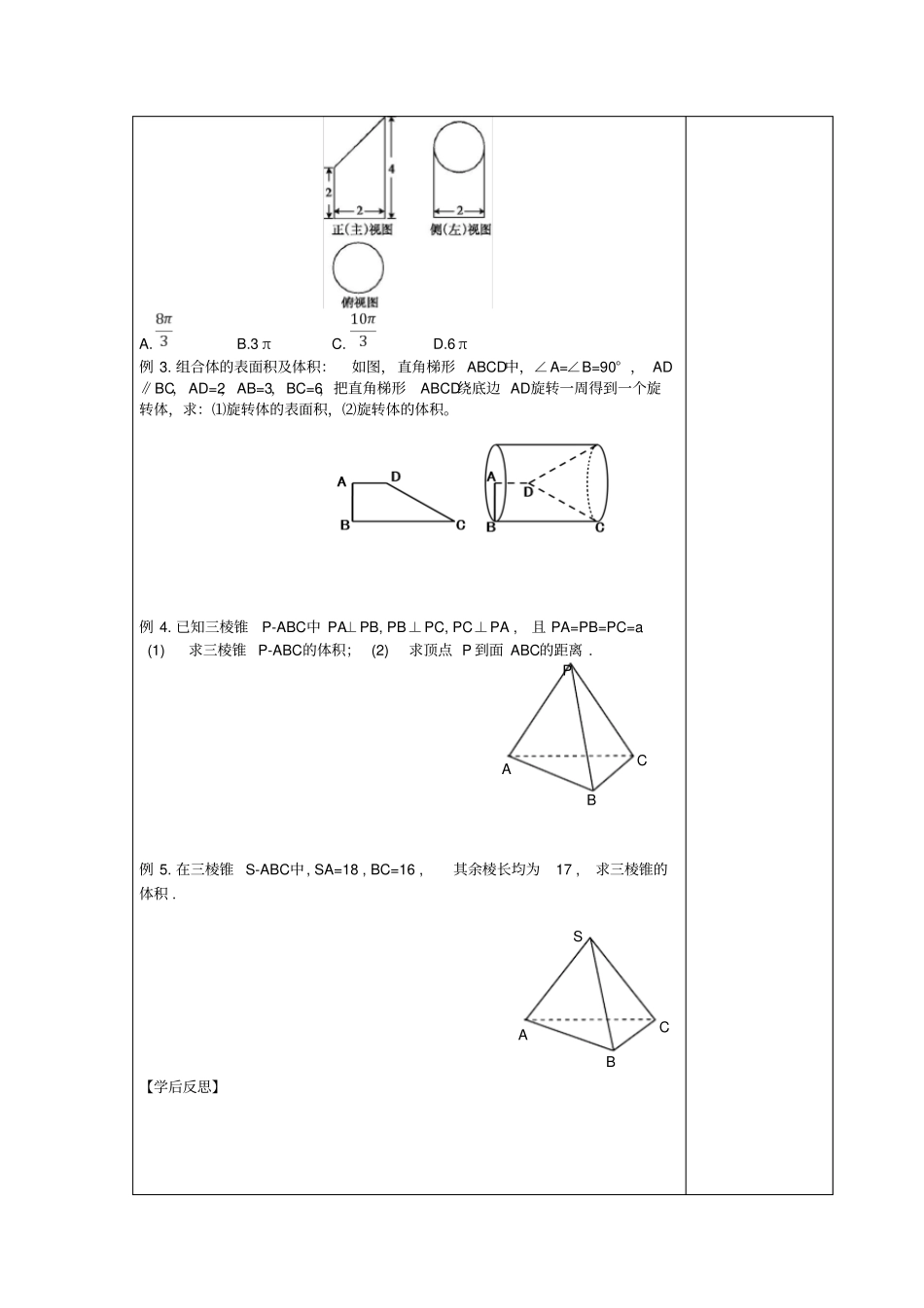
7.2棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积【教学目标】1.记住柱体、锥体、台体的体积的计算公式.2.会利用柱体、锥体、台体的体积公式解决一些简单的实际问题.【重点难点】求简单几何体的体积、球的表面积和体积。【教法教具】以讲学稿为依托的探究式教学方法,多媒体教学【教学课时】2课时【教学流程】■自主学习（课前完成，含独学和质疑）1．空间几何体的表面积与体积公式名称几何体表面积体积柱体(棱柱和圆柱)S表面积＝S侧＋2S底V＝Sh锥体(棱锥和圆锥)S表面积＝S侧＋S底V＝13Sh台体(棱台和圆台)S表面积＝S侧＋S上＋S下V＝13(S上＋S下＋S上S下)h2.一个正方体的体积是a,表面积是2a,则a等于().A.3B.6C.27D.543.半径为R的半圆卷成一个圆锥,这个圆锥的体积为.■合作探究：（对学、群学）例1.某几何体的三视图如图所示,则该几何体的体积为().A.B.C.200D.240例2.已知某几何体的三视图如图所示,则该几何体的体积为().备注：(教师二次备课栏或学生笔记栏)A.B.3πC.D.6π例3.组合体的表面积及体积：如图，直角梯形ABCD中，∠A=∠B=90°，AD∥BC，AD=2，AB=3，BC=6，把直角梯形ABCD绕底边AD旋转一周得到一个旋转体，求：⑴旋转体的表面积，⑵旋转体的体积。例4.已知三棱锥P-ABC中PA⊥PB,PB⊥PC,PC⊥PA,且PA=PB=PC=a(1)求三棱锥P-ABC的体积；(2)求顶点P到面ABC的距离.例5.在三棱锥S-ABC中,SA=18,BC=16,其余棱长均为17,求三棱锥的体积.【学后反思】PABCSABC【练案】1.如图，正四面体ABCD的棱长为6，P、Q分别是AC的中点、AD的三分之一点，则截面BPQ分正四面体上下两部分的体积之比等于；2.将边长为a的正方形ABCD沿对角线AC折起，使BD=a，则三棱锥D—ABC的体积为（）A．63aB．123aC．3123aD．3122a3．已知某几何体的左视图与其主视图相同，相关的尺寸如图所示，则这个几何体的体积是()A．8πB．7πC．2πD.7π44.如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积、体积分别是()A．32π，128π3B．16π，32π3C．12π，16π3D．8π，16π35．如图是某几何体的三视图，则该几何体的体积为()A．64＋32πB．64＋64πC．256＋64πD．256＋128π6.如图是某几何体的三视图,且主(正)视图、左(侧)视图、俯视图都是直角边长为2的等腰直角三角形,则该几何体的体积为.7.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积等于cm3.8.设正六棱锥的底面边长为1,侧棱长为,则它的体积是().A.6B.C.2D.29.如图所示,在长方体ABCD-A'B'C'D'中,用截面截下一个三棱锥C-A'DD',求三棱锥C-A'DD'的体积与剩余部分的体积之比.