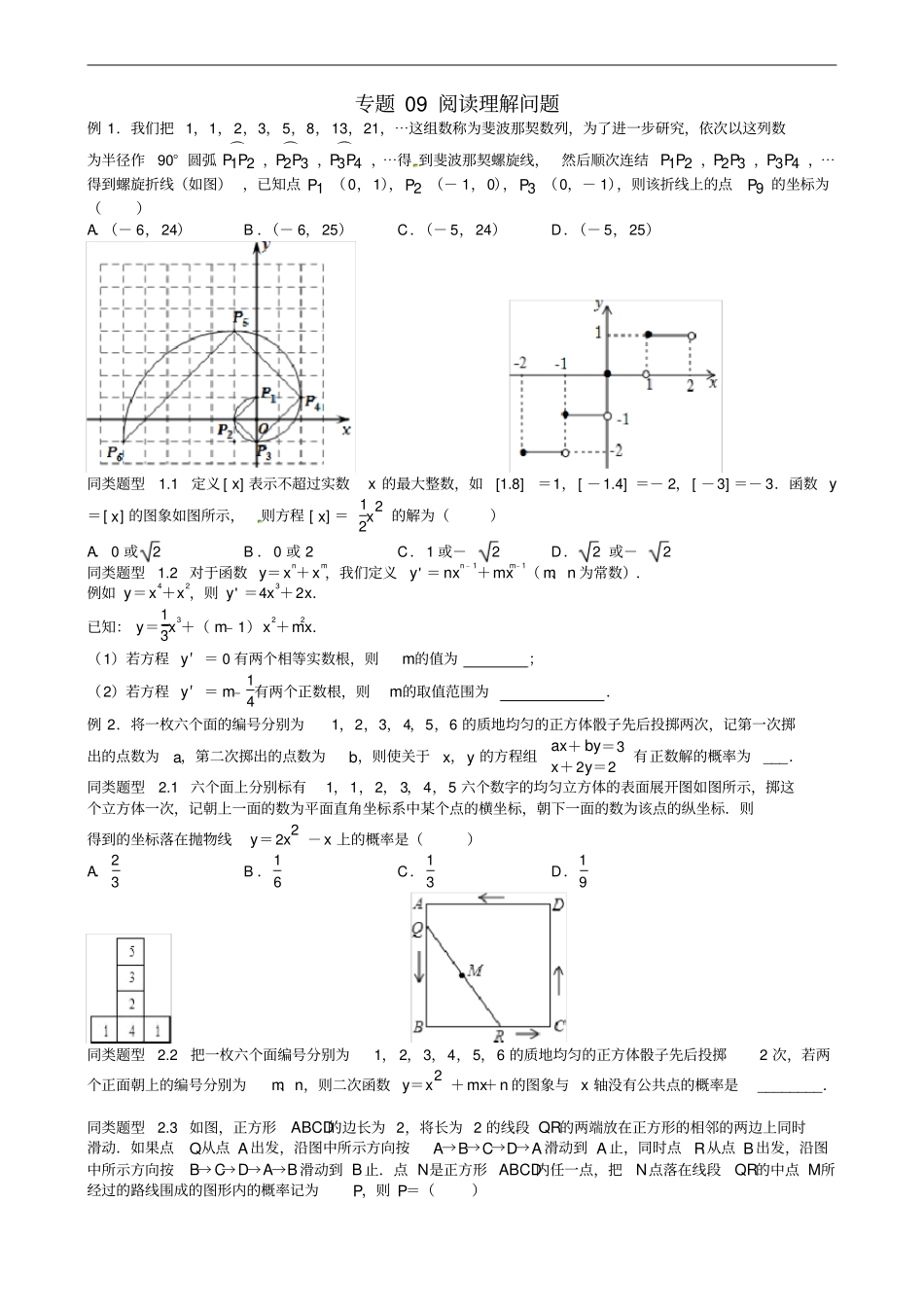
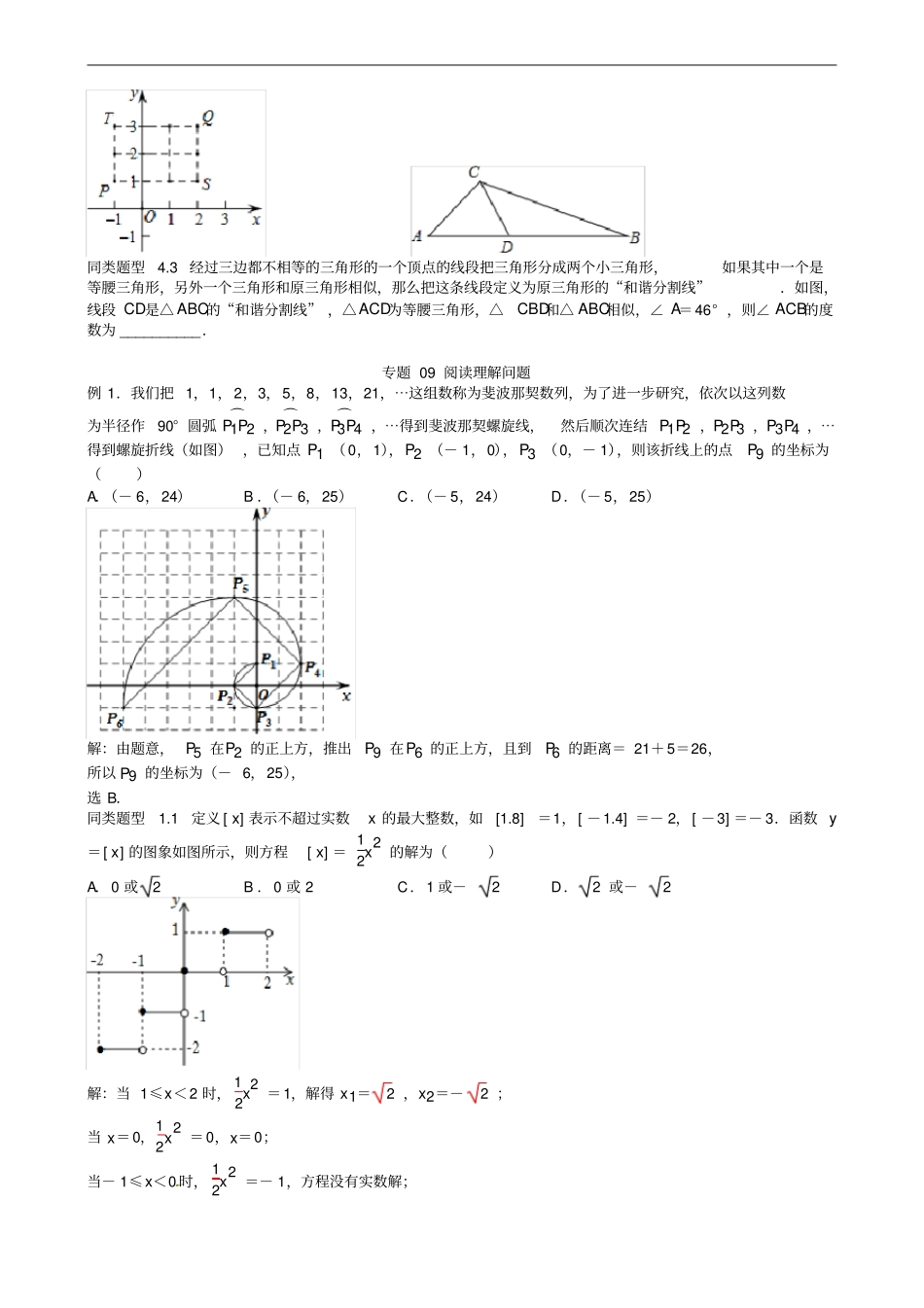
专题09阅读理解问题例1.我们把1,1,2,3,5,8,13,21,⋯这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧⌒P1P2,⌒P2P3,⌒P3P4,⋯得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,⋯得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为()A.(-6,24)B.(-6,25)C.(-5,24)D.(-5,25)同类题型1.1定义[x]表示不超过实数x的最大整数,如[1.8]=1,[-1.4]=-2,[-3]=-3.函数y=[x]的图象如图所示,则方程[x]=12x2的解为()A.0或2B.0或2C.1或-2D.2或-2同类题型1.2对于函数y=xn+xm,我们定义y'=nxn﹣1+mxm﹣1(m、n为常数).例如y=x4+x2,则y'=4x3+2x.已知:y=13x3+(m﹣1)x2+m2x.(1)若方程y′=0有两个相等实数根,则m的值为;(2)若方程y′=m﹣14有两个正数根,则m的取值范围为.例2.将一枚六个面的编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷两次,记第一次掷出的点数为a,第二次掷出的点数为b,则使关于x,y的方程组ax+by=3x+2y=2有正数解的概率为___.同类题型2.1六个面上分别标有1,1,2,3,4,5六个数字的均匀立方体的表面展开图如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数为该点的纵坐标.则得到的坐标落在抛物线y=2x2-x上的概率是()A.23B.16C.13D.19同类题型2.2把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m、n,则二次函数y=x2+mx+n的图象与x轴没有公共点的概率是________.同类题型2.3如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止.点N是正方形ABCD内任一点,把N点落在线段QR的中点M所经过的路线围成的图形内的概率记为P,则P=()A.4-π4B.π4C.14D.π-14同类题型2.4从-1,1,2这三个数字中,随机抽取一个数,记为a,那么,使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形的面积为14,且使关于x的不等式组x+2≤a1-x≤2a有解的概率为_________.例3.若f(n)为n2+1(n是任意正整数)的各位数字之和,如142+1=197,1+9+7=17,则f(14)=17,记f1(n)=f(n),f2=f(f1(n))⋯fk+1=fk(f(n)),k是任意正整数则f2016(8)=()A.3B.5C.8D.11同类题型3.1将1,2,3,⋯,100这100个自然数,任意分为50组,每组两个数,现将每组的两个数中任一数值记作a,另一个记作b,代入代数式12(|a-b|+a+b)中进行计算,求出其结果,50组数代入后可求得50个值,则这50个值的和的最大值是____________.同类题型3.2规定:[x]表示不大于x的最大整数,(x)表示不小于x的最小整数,[x)表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2.则下列说法正确的是________.(写出所有正确说法的序号)①当x=1.7时,[x]+(x)+[x)=6;②当x=-2.1时,[x]+(x)+[x)=-7;③方程4[x]+3(x)+[x)=11的解为1<x<1.5;④当-1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有两个交点.同类题型3.3设[x]表示不大于x的最大整数,{x}表示不小于x的最小整数,<x>表示最接近x的整数(x≠n+0.5,n为整数).例如[3.4]=3,{3.4}=4,<3.4≥3.则方程3[x]+2{x}+<x≥22()A.没有解B.恰好有1个解C.有2个或3个解D.有无数个解同类题型3.4对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{-2,-3}=______;若min{(x-1)2,x2}=1,则x=____________.例4.已知点A在函数y1=-1x(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1,y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为()A.有1对或2对B.只有1对C.只...