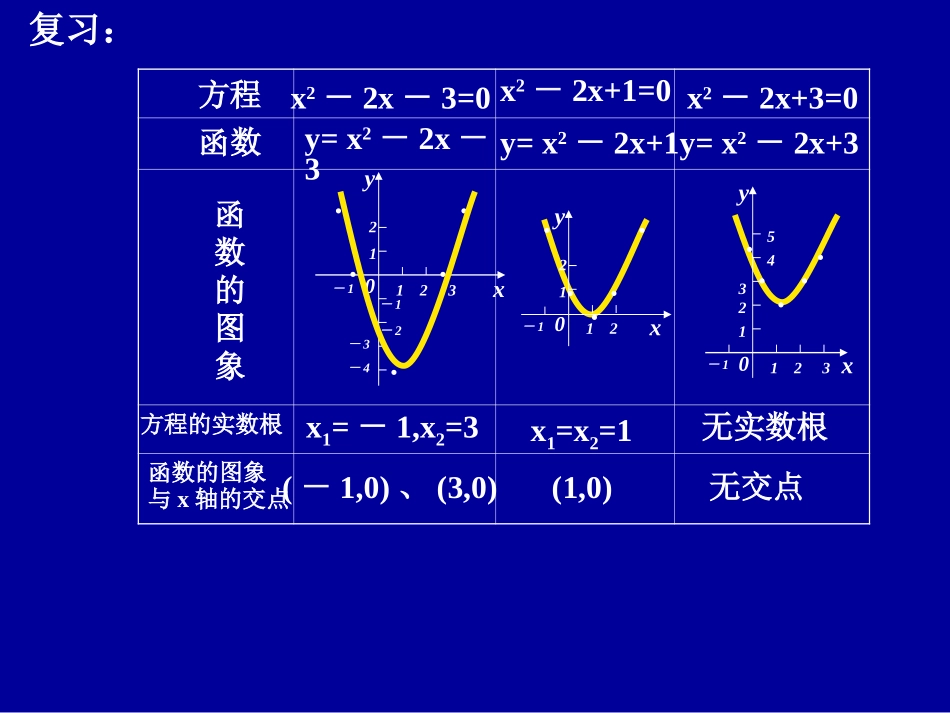
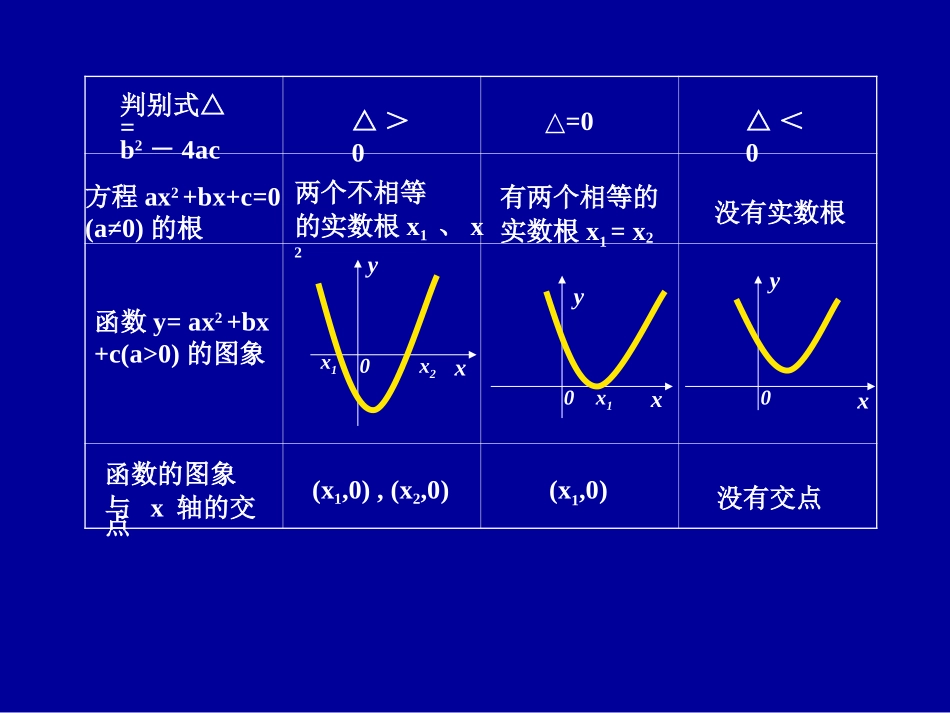
方程的根与函数的零点方程x2-2x+1=0x2-2x+3=0y=x2-2x-3y=x2-2x+1函数函数的图象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0xy0-132112-1-2-3-4...............y=x2-2x+3复习:yx0-12112xy0-132112543方程ax2+bx+c=0(a≠0)的根函数y=ax2+bx+c(a>0)的图象判别式△=b2-4ac△>0△=0△<0函数的图象与x轴的交点有两个相等的实数根x1=x2没有实数根xyx1x20xy0x1xy0(x1,0),(x2,0)(x1,0)没有交点两个不相等的实数根x1、x2小结:一元二次方程ax2+bx+c=0(a≠0)的根是二次函数y=ax2+bx+c(a≠0)图象与x轴交点的横坐标.推广:你能类比描述出方程f(x)=0的根与相应函数y=f(x)图象与x轴交点的关系吗?方程f(x)=0的根是相应函数y=f(x)图象与x轴交点的横坐标.一零点定义:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.二等价关系:方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点例2:求下列函数的零点(1)f(x)=lgx(2)f(x)=2x例1:函数f(x)=x2-2x+1的零点是()A(1,0)B(-1,0)C1D-1c1二次函数f(x)=x2-2x-3的图象如图所示:f(-2)·f(1)(<或>)0.在区间(-2,1)内(有或无)零点.....xy0-132112-1-2-3-4-24f(2)·f(4)(<或>)0.在区间(2,4)内(有或无)零点练习:<有<有2函数y=f(x)的图象如图所示:f(a)·f(b)(<或>)0.在区间(a,b)内(有或无)零点f(c)·f(d)(<或>)0.在区间(c,d)内(有或无)零点f(b)·f(c)(<或>)0.在区间(b,c)内(有或无)零点探究:函数y=f(x)在区间(a,b)内满足什么条件时存在零点?<<<有有有三零点存在性定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c(a,∈b),使得f(c)=0,这个c也就是方程f(x)=0的根。-4-1.30691.09863.38635.60947.79189.945912.079414.1972例3求函数f(x)=lnx+2x-6的零点个数。123456789xxff((xx))解:..................x0-2-4-6105y241086121487643219)11,10()10,9()9,8()8,7()(09lgDCBAxx:的根所在的大致区间是方程变式题:C小结:1函数零点的定义;22等价关系;等价关系;3零点存在性定理.