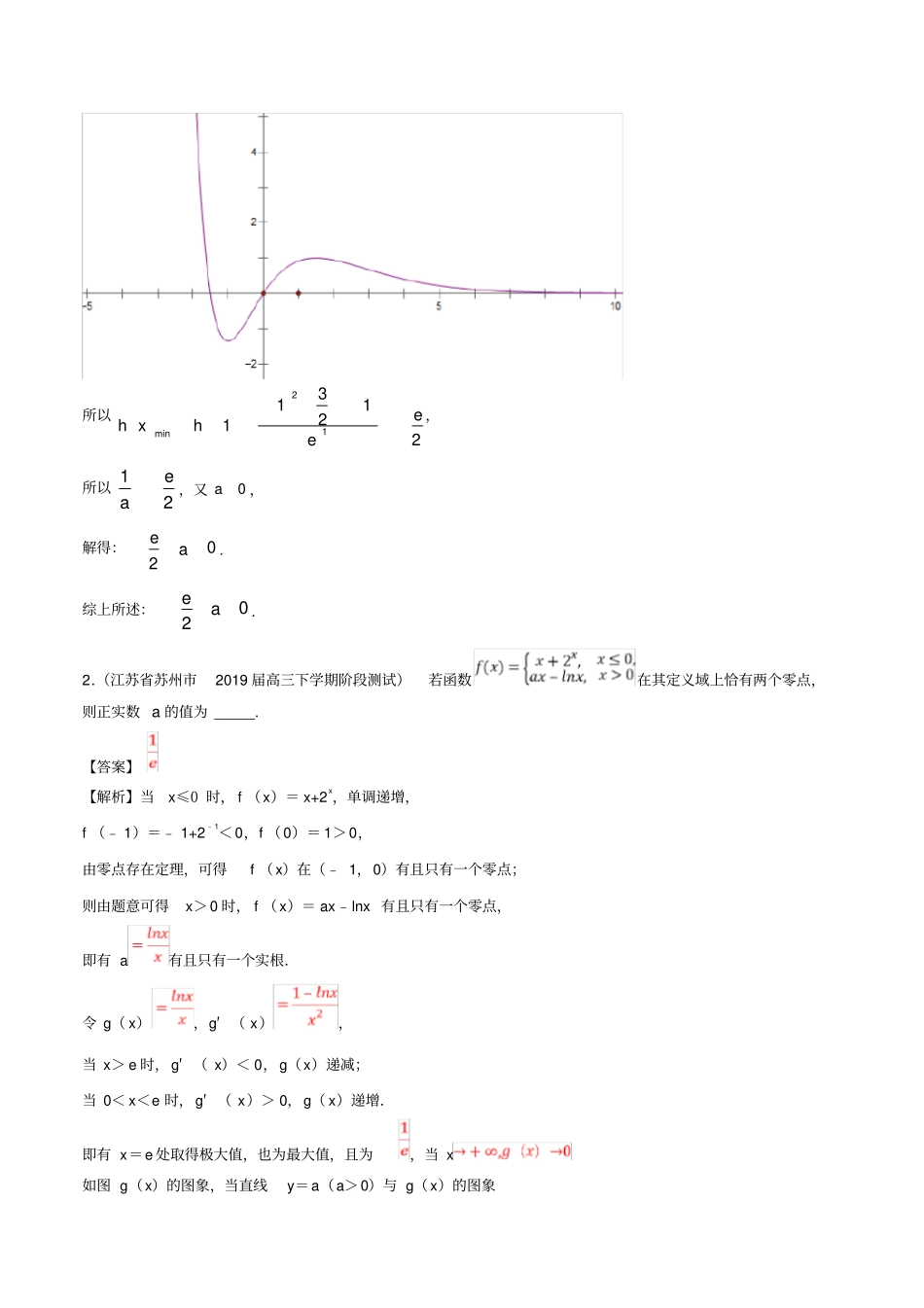
考点14导数的应用1.(江苏省苏锡常镇四市2019届高三教学情况调查二)已知e为自然对数的底数,函数2xfxeax的图像恒在直线32yax上方,则实数a的取值范围为_______.【答案】12,0e【解析】因为函数2xfxeax的图像恒在直线32yax上方,所以xR,232xeaxax恒成立,即:232xeaxx恒成立.当0a时,若x,0xe,232axx,不满足232xeaxx恒成立.当0a时,23020xexx恒成立.当0a时,不等式232xeaxx恒成立等价于:2min312xxxae,记232xxxehx,则312xhxexx,此时,hx在,1上递减,在31,2上递增,在3,2上递减,其简图如下:所以12min131122ehxhe,所以12ae,又0a,解得:02ea.综上所述:02ea.2.(江苏省苏州市2019届高三下学期阶段测试)若函数在其定义域上恰有两个零点,则正实数a的值为_____.【答案】【解析】当x≤0时,f(x)=x+2x,单调递增,f(﹣1)=﹣1+2﹣1<0,f(0)=1>0,由零点存在定理,可得f(x)在(﹣1,0)有且只有一个零点;则由题意可得x>0时,f(x)=ax﹣lnx有且只有一个零点,即有a有且只有一个实根.令g(x),g′(x),当x>e时,g′(x)<0,g(x)递减;当0<x<e时,g′(x)>0,g(x)递增.即有x=e处取得极大值,也为最大值,且为,当x如图g(x)的图象,当直线y=a(a>0)与g(x)的图象只有一个交点时,则a.故答案为:.3.(江苏省扬州市2018-2019学年度第一学期期末检测试)若存在正实数x,y,z满足,且,则的最小值为_______.【答案】【解析】【分析】由?,又lnln()=lnlneln,令,则lnelnet﹣lnt,t,f(t)=et﹣lnt,利用函数求导求最值.【详解】 正实数x,y,z满足3y2+3z2≤10yz,∴?, ,∴lne,lnln()=lnlneln,令,则lnelnet﹣lnt,t,f(t)=et﹣lnt,f′(t)=e0,则t,可得f(t)在()递减,在()递增,∴f(t)min=f()=1﹣(﹣1)=2,即(ln)min=2,∴的最小值为e2,故答案为:e2.4.(江苏省徐州市(苏北三市(徐州、淮安、连云港))2019届高三年级第一次质量检测)已知,,,且,则的最小值为_________.【答案】【解析】令,,,,在上递减,在上递增,所以,当时,有最小值:所以,的最小值为故答案为:.5.(江苏省七市(南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019届高三第三次调研考试)已知数列满足(),().(1)若,证明:是等比数列;(2)若存在,使得,,成等差数列.①求数列的通项公式;②证明:.【答案】(1)见解析;(2)①,②见解析【解析】(1)由,得,得,即,因为,所以,所以(),所以是以为首项,2为公比的等比数列.(2)①设,由(1)知,,所以,即,所以.因为,,成等差数列,则,所以,所以,所以,即.②要证,即证,即证.设,则,且,从而只需证,当时,.设(),则,所以在上单调递增,所以,即,因为,所以,所以,原不等式得证.6.(江苏省苏锡常镇四市2019届高三教学情况调查二)已知数列na,12a,且211nnnaaa对任意nN恒成立.(1)求证:112211nnnnaaaaaaL(nN);(2)求证:11nnan(nN).【答案】(1)见解析(2)见解析【解析】(1)①当1n时,2221112213aaa满足211aa成立.②假设当nk时,结论成立.即:112211kkkkaaaaaaL成立下证:当1nk时,112211kkkkaaaaaaL成立。因为211211111kkkkkaaaaa11221112211111kkkkkkkkaaaaaaaaaaaaLL即:当1nk时,112211kkkkaaaaaaL成立由①、②可知,112211nnnnaaaaaaL(n*N)成立。(2)(ⅰ)当1n时,221221311a成立,当2n时,2322222172131112aaaaa成立,(ⅱ)假设nk时(3k),结论正确,即:11kkak成立下证:当1nk时,1211kkak成立.因为2211112111111kkkkkkkkkaaaaakkkk要证1211kkak,只需证12111kkkkkk只需证:121kkkk,只需证:12lnln1kkkk即证:12llnn10kkkk(3k)记2ln11lnhxxxxx2ln1112ln11lnlnxxxxhx21ln1ln12111xxxx当12x≥时,1111ln121ln221ln1ln10122xxe所以2ln11lnhxxxxx在1,上递增,又6423ln34ln3ln34ln729ln2564l0nh所以,当3x时,30hxh恒成立。即:当3k时,30hkh成立。即:当3k时,12llnn10kkkk恒成立.所以当3k,1211kkak恒成立.由(ⅰ)(ⅱ)可得:对任意的正整数nN,不等式11nnan恒成立,命题得证.7.(江苏省苏锡...