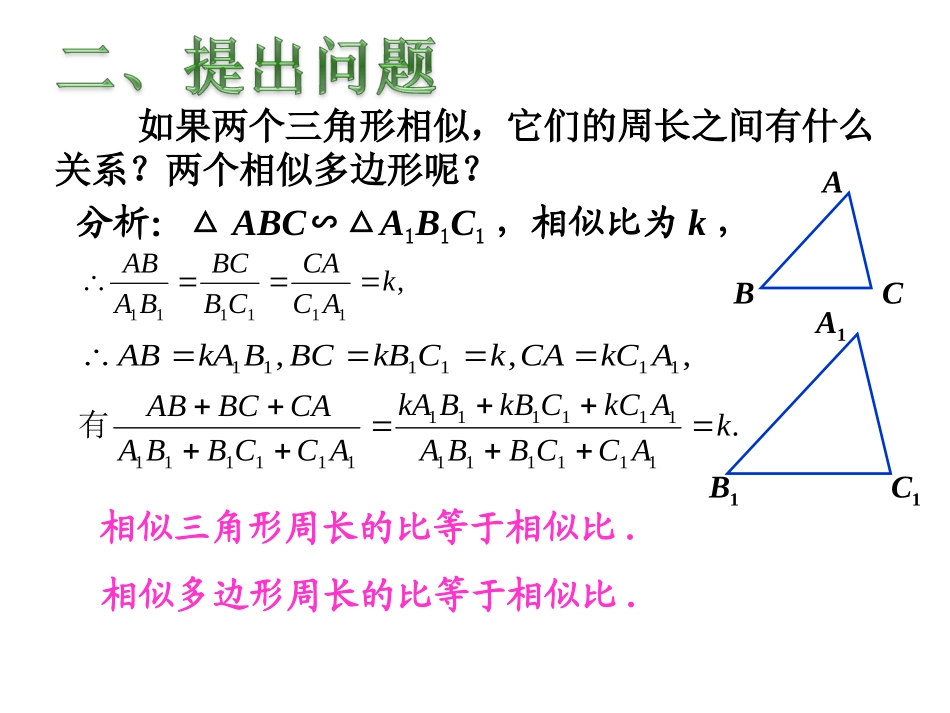
第二十七章相似27.2.327.2.3相似三角形的周长与面积相似三角形的周长与面积相似三角形的判定方法:1.相似三角形的定义:对应角相等、对应边成比例的三角形叫做相似三角形.(SSS)(AA)(SAS)(HL)2.相似多边形的对应角、对应边的性质.相似多边形的对应角相等、对应边成比例.如果两个三角形相似,它们的周长之间有什么关系?两个相似多边形呢?相似三角形周长的比等于相似比.相似多边形周长的比等于相似比.ABCA1B1C1分析:△ABC∽△A1B1C1,相似比为k,,111111kACCACBBCBAAB,,,111111AkCCAkCkBBCBkAAB.111111111111111111kACCBBAAkCCkBBkAACCBBACABCAB有(1)如图,△ABC∽△A′B′C′,相似比为k1,它们对应高的比是多少?面积比是多少?相似三角形对应高的比等于相似比.ABCA′B′C′如图,分别作出△ABC和△A′B′C′的高AD和A′D′.∵△ABC和△A′B′C′都是直角三角形,并且∠B=∠B′,∴△ABD∽△A′B′D′..BAABDAAD∵△ABC∽△A′B′C′..CBBCBAAB.kDAADDD′(1)如图,△ABC∽△A′B′C′,相似比为k1,它们对应高的比是多少?面积比是多少?相似三角形面积比等于相似比的平方.ABCA′B′C′.21212111kkkDAADCBBCDACBADBCSSCBAABC△△DD′(2)如图,四边形ABCD相似于四边形A′B′C′D′,相似比为k2,它们面积的比是多少?相似多边形面积比等于相似比的平方.ABCA′B′C′DD′如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D,△ABC的周长是24,面积是,求△DEF的周长和面积.512ABCDEF1.判断:(1)一个三角形的各边长扩大为原来的5倍,这个三角形的周长也扩大为原来的5倍.()(2)一个四边形的各边长扩大为原来的9倍,这个四边形的面积也扩大为原来的9倍.()2.如图,△ABC∽△A′B′C′,它们的周长分别为60和72,且AB=15,B′C′=24,求BC,AC,A′B′,A′C′的长.ABCA′B′C′对不对说说你在本节课的收获.1.必做题:教材第53页练习第3、4题.2.选做题:教材第56页习题27.2第12、13、14题.3.备选题:如图,已知矩形ABCD的边长AB=2,BC=3,点P是AD边上的一动点(P异于A、D),Q是BC边上的任意一点.连AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.(1)求证:△APE∽△ADQ;(2)设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值,最大值为多少?(3)当Q在何处时,△ADQ的周长最小?(只需给出确定Q在何处的过程或方法,不必给出证明)