培养审题习惯提高分析能力VIP免费

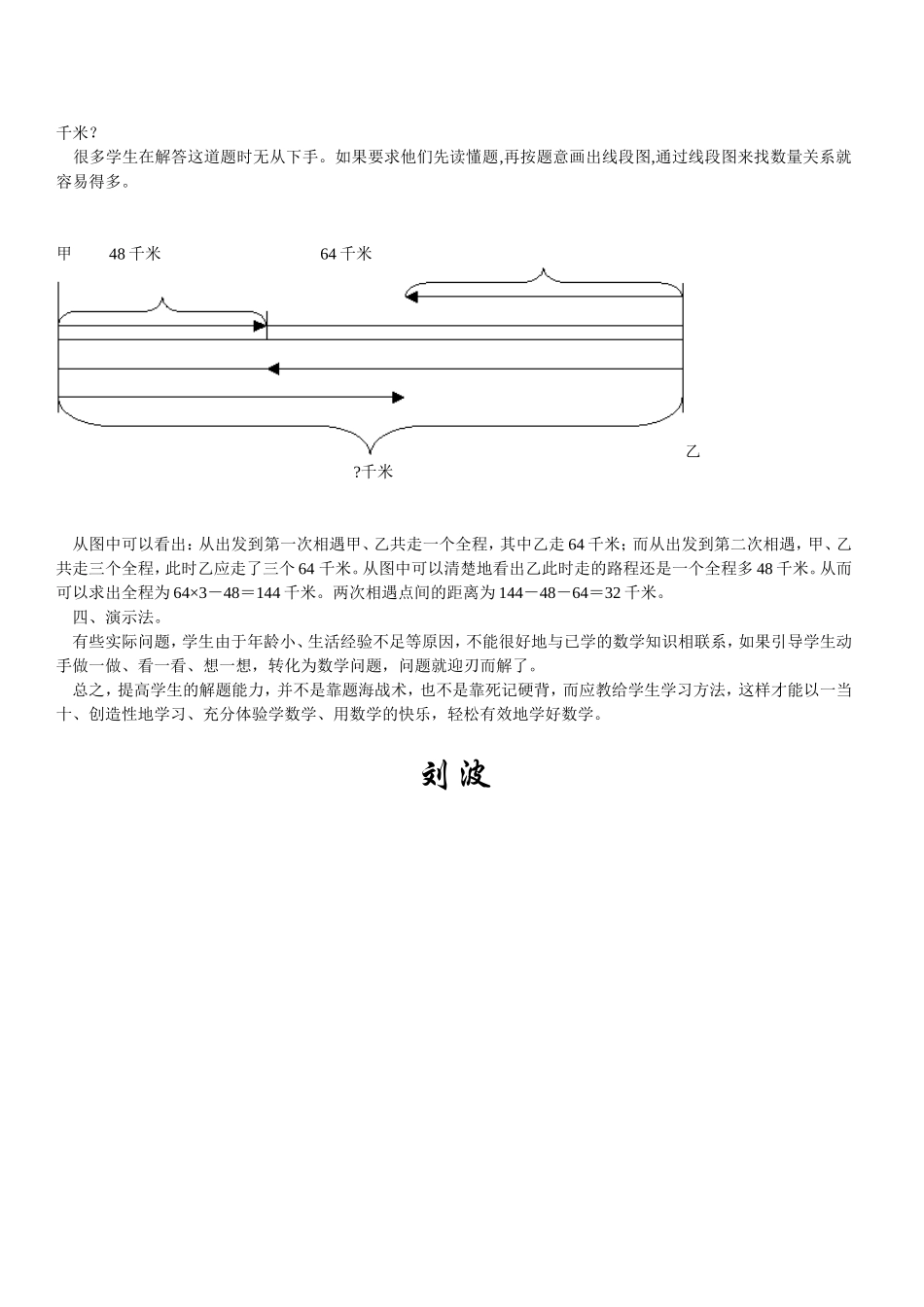
培养审题习惯提高分析能力在教学实践中，我深深地体会到：培养学生的审题习惯、提高分析能力对提高学生的解题能力尤为重要，而且行之有效。学生在解题时，往往会因为没有读懂题、没有注意题中的重点词句而做错题，或因不能找出题中的数量关系而不会解题。针对学生的实际，我要求学生在做题之前要多读题、读懂题，并要求他们读题时找出解这道题应注意的问题，允许他们在题中的重点词句下作记号。如：见到圆锥就要想“”;与计量单位有关的问题要注意单位是否统一；分数乘除法应用题要找准单位“1”和对应关系；而像“实际每天多修0.12千米”不要当成了“实际每天修0.12千米”……在审题时，就提醒自己应注意哪些问题，做到心中有数，不要犯一些低级错误。即使是做计算题也要审好题，要观察好题中有哪些计算、能否简便、怎样简便、不能简便又应先算什么。如果不审题，做计算题不仅费时，而且容易出错，不能达到又快又准的目的。学生审完题后，有些题数量关系较复杂，如果不善于分析，解答起来依然有困难。而引导学生掌握正确的分析方法，可以帮助他们找出题中的数量关系，突破难点，化难为易。我常给学生介绍以下几种方法来找数量关系。一、直译法。如：有些学困生对“某数的比120的20％多24，求某数。”这样的逆向思考的问题感觉到困难，我就帮他们通过将某数设为x，将题目直译成一个等式，先找出谁多（x）谁少（120的20％），它们相差24即x－120×20％＝24，这样，他们解答起来就容易得多。二、摘录法。有些题目将条件、问题摘录之后，数量关系就能较直观地呈现出来，也不容易出现张冠李戴的错误。如：一个晒盐场用100克海水可以晒出3克盐，如果一个盐池一次放入5800吨海水，可以晒出多少吨盐？读题后摘录如下：海水晒盐100克3克5800吨？吨通过摘录，不仅理清了题中的对应关系，也便于看清题中的单位不统一等问题，可以帮助学生更好地用比例、出盐率、倍数等不同的方法来正确解题。再如：一个圆柱的体积和圆锥的体积相等，已知圆柱的高是圆锥的，圆柱的底面积是圆锥的几分之几？这种题很多学生由于没有正确地分析数量关系，解答起来容易出错。如果将条件、问题摘录出来，就容易找出数量关系。圆柱圆锥体积：1：1高：2：5底面积：（）：（）从而，可以算出圆柱的底面积为：1÷2=,圆锥的底面积为：1×3÷5＝。所以，÷＝。三、图示法。在解答分数应用题、行程问题等多种问题时，都可以通过线段图来帮助学生分析数量关系。如：甲、乙两车同时从A、B两地出发相向而行，两车在离B地64千米处第一次相遇，相遇后两车仍以原速继续行驶，并且在到达对方出发点后，立即沿原路返回，途中两车在距A48千米处第二次相遇，问两次相遇点相距多少千米？很多学生在解答这道题时无从下手。如果要求他们先读懂题,再按题意画出线段图,通过线段图来找数量关系就容易得多。甲48千米64千米乙?千米从图中可以看出：从出发到第一次相遇甲、乙共走一个全程，其中乙走64千米；而从出发到第二次相遇，甲、乙共走三个全程，此时乙应走了三个64千米。从图中可以清楚地看出乙此时走的路程还是一个全程多48千米。从而可以求出全程为64×3－48＝144千米。两次相遇点间的距离为144－48－64＝32千米。四、演示法。有些实际问题，学生由于年龄小、生活经验不足等原因，不能很好地与已学的数学知识相联系，如果引导学生动手做一做、看一看、想一想，转化为数学问题，问题就迎刃而解了。总之，提高学生的解题能力，并不是靠题海战术，也不是靠死记硬背，而应教给学生学习方法，这样才能以一当十、创造性地学习、充分体验学数学、用数学的快乐，轻松有效地学好数学。刘波