§10.2---感应电动势VIP免费

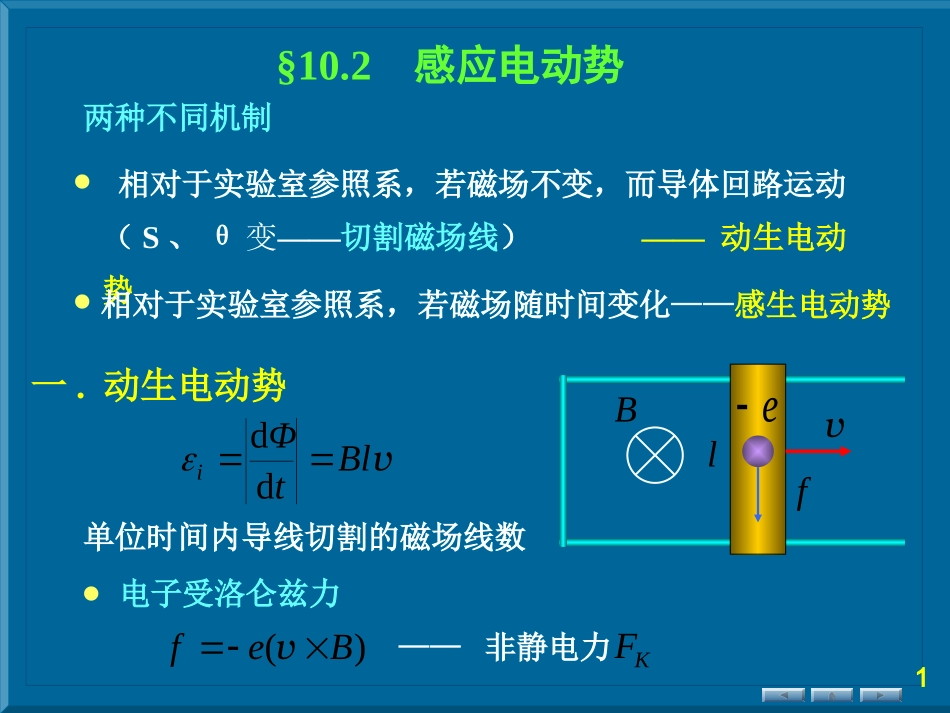
§10.2感应电动势两种不同机制相对于实验室参照系，若磁场不变，而导体回路运动（S、θ——变切割磁场线）——动生电动势相对于实验室参照系，若磁场随时间变化——感生电动势一.动生电动势Blvf单位时间内导线切割的磁场线数)(Befv电子受洛仑兹力——非静电力KFevBltΦidd•••1非静电场eFEKKBv动生电动势应用ld磁场中的运动导线成为电源，非静电力是洛仑兹力vlBablEKidlBd)(vlBid)(vlBabdvBlv••2lBdv判断下列导线ab是否产生动生电动势01i、bavB02Bv、0bavBbavldBv)(4、0bavldBv)(3、03ba0)5(、boabaO0、)6(讨论(2)对于运动导线回路，电动势存在于整个回路lBid)(v)d(lBvtltB)/ΔdΔ(vtSB/'dt/Φ(法拉第电磁感应定律)4(3)感应电动势的功率设电路中感应电流为IBvab导线受安培力导线匀速运动电路中感应电动势提供的电能是由外力做功所消耗的机械能转换而来的(4)感应电动势做功，洛仑兹力不做功？BvfV'fFVF)()(''ffvvvv''ffvvvvBeBe''0e'vvIBlIPiIBlFmmextFFvvIBlFPextextPmFextFI洛仑兹力做功为零vBefBvefVF5例1在匀强磁场B中，长R的铜棒绕其一端O在垂直于B的平面内转动，角速度为BOR求棒上的电动势解方法一(动生电动势):dlAAOilBd)(vROlBdvROlBld22BR方向：OA方法二(法拉第电磁感应定律):Φd在dt时间内导体棒切割磁场线vdBRd212tΦiddtBRdd212221BR6OAUU导体圆盘情况又如何呢？例2在半径为R的圆形截面区域内有匀强磁场B，一直导线垂直于磁场方向以速度v扫过磁场区。求当导线距圆心为r时的动生电动势vBrRab解方法一：动生电动势bailBd)(vldbalBdv)(abBv222rRBvO方法二：法拉第电磁感应定律在dt时间内导体棒切割磁场线rBrRΦd2d22trrRBtΦidd2dd22222rRBv7xxBxIB20ovaLIdx例3在通有电流I的无限长载流直导线旁，距a垂直放置一长为L以速度v竖直向上运动的导体棒，求导体棒中的动生电动势。解1：建立图示座标系，在距坐标原点o处取导体线元，则vBdxidxBvd)(0ln2200aLaIvxdxIvLaa<0，其方向与假设方向相反，即为x轴负向，左端电势高LaavBdx8idxld解2：利用法拉第电磁感应定律计算。引入辅助线构成图示假想矩形回路。t时刻回路高为vt、宽为L。假设回路所围平面正法向与磁场同向（电动势和回路绕向为顺时针方向）。将回路分割成无限多长为vt、宽为dx的面元，穿过面元的磁通量为：vadxyBvtdxxIsdBd20ILaLaIvtxdxIvtaLaln22000ln20aLaIvdtd<0，方向与假设方向相反，即为逆时针方向（x轴负向，左端电势高）9解题方法总结解题方法总结确定磁场B；建立适当的坐标系；选取线元dl，确定vB（电动势）方向和dl取向的关系；设dl方向为电动势方向(积分方向)；由动生电动势公式计算，如>0，则其方向与假设方向相同，反之则相反。LldBv10二.感生电动势实验证明：当磁场变化时，静止导体中也出现感应电动势仍是洛仑兹力充当非静电力？电场力充当非静电力麦克斯韦提出：无论有无导体或导体回路，变化的磁场都将在其周围空间产生具有闭合电场线的电场，并称此为感生电场或有旋电场。感生电动势VEbaVilEd闭合回路中是感生电场tΦlELVidddSSBtddd•11SSdtBddSSdtBdd感生电场与变化磁场之间的关系讨论感生电场与静电场的比较场源环流LVlEd＝静止电荷变化的磁场通量静电场为保...