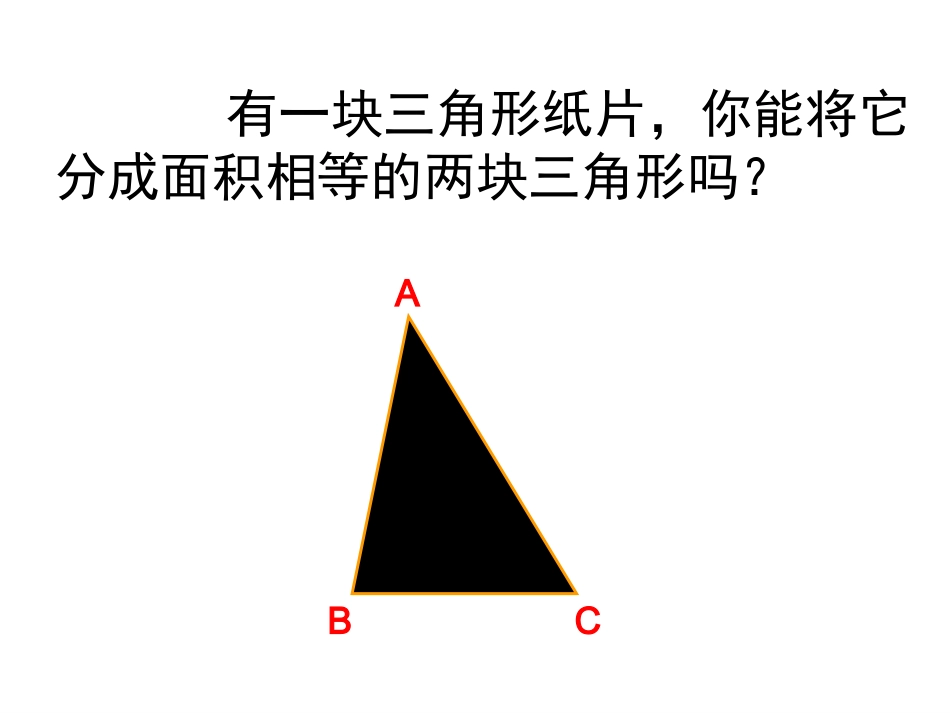
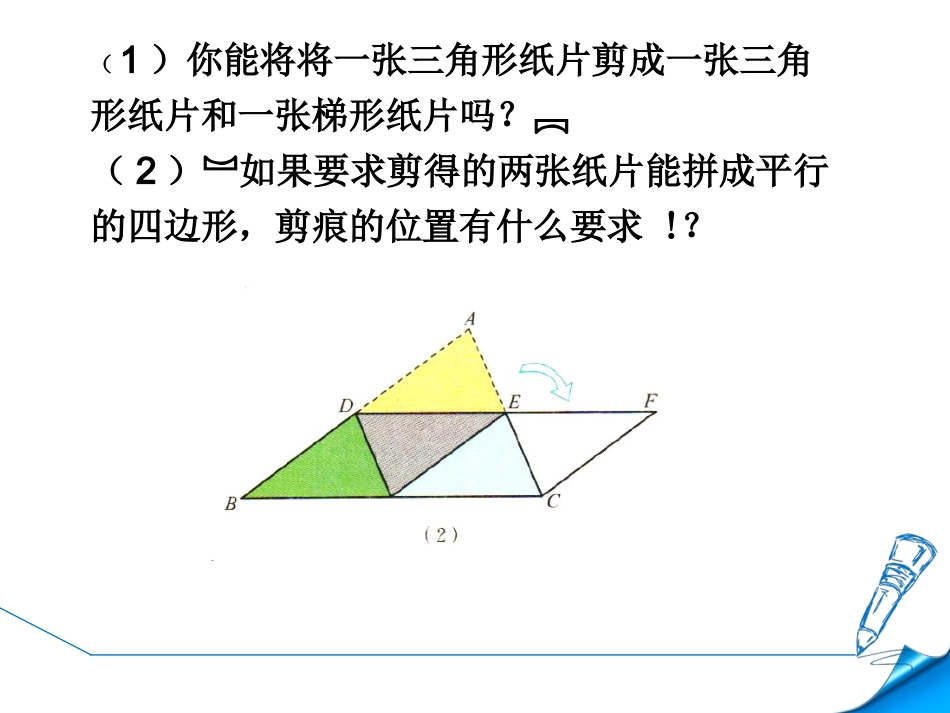
2013.11.14ABC有一块三角形纸片,你能将它分成面积相等的两块三角形吗?(1)你能将将一张三角形纸片剪成一张三角形纸片和一张梯形纸片吗?(2)如果要求剪得的两张纸片能拼成平行的四边形,剪痕的位置有什么要求?连接三角形两边中点的线段叫做三角形的中位线.归纳ABC中点D中点E一个三角形有几条中位线?F:连结三角形两边中点的线段叫做三角形的中位线。几何语言:∵点D、E分别是AB和AC的中点∴DE是△ABC的中位线定义(1)相同之处——都和边的中点有关;(2)不同之处:三角形中位线的两个端点都是边的中点;三角形中线只有一个端点是边的中点,另一端点是三角形的顶点。CBAED概念对比CBAD中线DC中位线DE123能准确叙述、证明三角形中位线定理会运用中位线定理解决相关问题经历探索、猜想、证明的过程,进一步发展推理论证能力学习目标:三角形中位线定理的证明方法合作交流FFG探究三角形中位线定理的证明方法12如图(2),延长DE到F,使FE=DE,连接CF.在△ADE和△CFE中,∵AE=CE,∠1=∠2,DE=FE,∴△ADE≌△CFE.∴∠A=∠ECF,AD=CF.证明:已知:如图(1),DE是△ABC的中位线.求证:DE∥BC,DE=BC.∴CF∥AB.∵BD=AD,∴CF=BD.∴四边形DBCF是平行四边形(一组对边平行且相等的四边形是平行四边形).∴DF∥BC(平行四边形的定义),DF=BC(平行四边形的对边相等).∴DE∥BC,DE=BC.12三角形的中位线平行于第三边,且等于第三边的一半.三角形中位线定理∵DE是△ABC的中位线∴DE∥BC(位置关系)(数量关系)用几何语言可表示为:DE=BC12(1)我想测量一池塘的宽度,能不能用三角形中位线知识设计一个方案,并说明这样做的理由.完成.p152随堂练习2应用(2)求证:三角形的一条中位线平分第三边上的中线.1、已知:DE是在△ABC中位线,则(1)若∠ADE=65°,则∠B=____度.(2)若BC=12cm,则DE=_____cm.(3)若DE=7cm,则BC=______cm.656分层训练A14分层训练B4(1)图中共有_____个平行四边形,与△DEF全等的三角形有_____个(2)若CDEF△=3,则CABC△=____(3)若SDEF△=6,则SABC△=_____332463、已知:点D,E,F分别是△ABC三边的中点,则DCBAHGFE4、已知:如图,在四边形ABCD中E,F,G,H分别为各边的中点,求证:四边形EFGH是平行四边形.分层训练C知识小结知识产生过程课堂小结知识方面学法指导数学思想方法