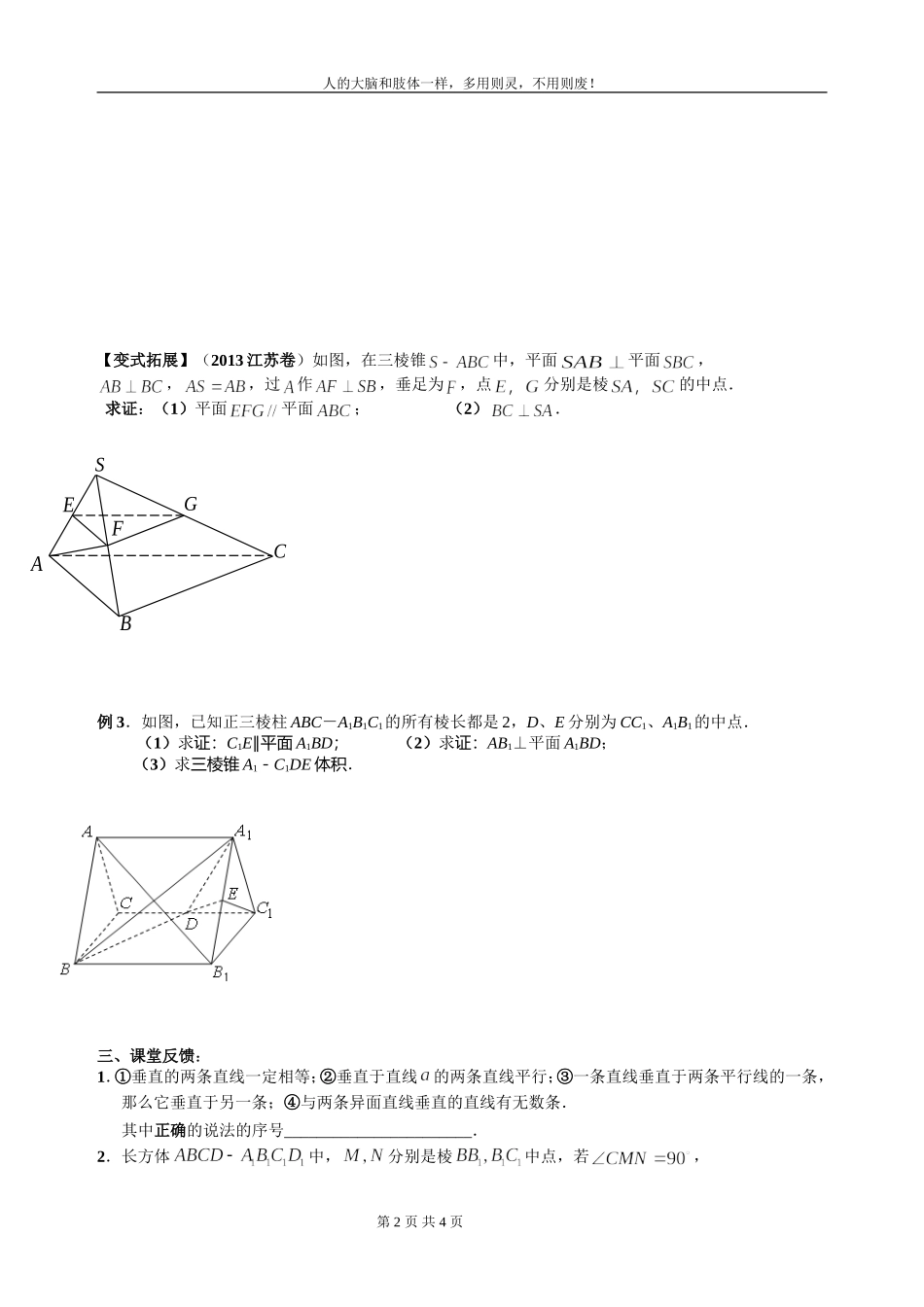
BADCFE句容三中2013—2014学年度第一学期高二数学教学案必修2第1章立体几何第18份总第31份2013-10-30立体几何复习课(1)主备人:吕金勇检查人:吴万征行政审核人:李才林【教学目标】了解空间线面平行、垂直的概念,能正确地判断空间线线、线面与面面的位置关系【教学重点】运用线面、面面平行、垂直的判定定理和性质定理.【教学难点】运用定理证明一些简单的垂直关系.【教学过程】一、引入:1.已知直线和平面,下列推理错误的是.①且;②∥且;③∥且∥;④且∥或a.2.已知a,b,c是直线,β是平面,给出下面命题:①若a⊥b,b⊥c,则a∥c;②若a∥c,b⊥c,则a⊥b;③若a∥β,b⊂β,则a∥b;④若a与b异面,且a∥β,则b与β相交;⑤若a与b异面,则至多有一条直线与a、b都垂直.其中正确命题的序号是_____________.3.考察下列三个命题,在“________”处都缺少同一个条件,补上这个条件使其构成真命题(其中l、m为直线,α、β为平面),则此条件为_______________.①⇒l∥α;②⇒l∥α;③⇒l∥α.二、新授内容:例1.在三棱锥中,平面,为正三角形,、分别是、中点,设.(1)证明:面面;(2)如何在上找一点,使面,说明理由.例2.如图,在四棱锥EABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,反思:90AEB,BEBC,F为CE的中点.求证:(1)AE∥平面BDF;(2)平面BDF平面ACE.第1页共4页BCPAED人的大脑和肢体一样,多用则灵,不用则废!【变式拓展】(2013江苏卷)如图,在三棱锥中,平面平面,,,过作,垂足为,点分别是棱的中点.求证:(1)平面平面;(2).例3.如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点.(1)求证:C1E∥平面A1BD;(2)求证:AB1⊥平面A1BD;(3)求三棱锥A1-C1DE体积.三、课堂反馈:1.①垂直的两条直线一定相等;②垂直于直线的两条直线平行;③一条直线垂直于两条平行线的一条,那么它垂直于另一条;④与两条异面直线垂直的直线有无数条.其中正确的说法的序号_______________________.2.长方体中,分别是棱中点,若,第2页共4页ABCSGFEACEFHGBD句容三中2013—2014学年度第一学期高二数学教学案必修2第1章立体几何第18份总第31份2013-10-30则异面直线和所成角_____________.3.在直三棱柱111ABCABC中,E、F分别是1AB、1AC的中点,点D在11BC上,11ADBC.求证:(1)EF∥平面ABC;(2)平面1AFD平面11BBCC.四、课后作业:学生姓名:___________1.若a、b表示直线,α表示平面,下列命题中正确的有________个.①a⊥α,b∥α⇒a⊥b;②a⊥α,a⊥b⇒b∥α;③a∥α,a⊥b⇒b⊥α.2.以下四个命题:其中不正确的序号是____________.①若//则//;②若//则//;③若////则//;④若////则//.3.下列命题正确的序号是.(其中表示直线,表示平面)①若;②若;③若;④若.4.已知,,是三个互不重合的平面,是一条直线,给出下列四个命题:①若,l,则//l;②若,//ll,则;③若上有两个点到的距离相等,则//l;④若,//,则.其中正确命题的序号是.5.为三条不同的直线,为三个不同的平面,则下列四个命题:(1),则;(2),则;(3),则;(4),则.其中正确的序号是.6.设a、b是不同的直线,α、β是不同的平面,则下列四个命题中正确的是.①若a⊥b,a⊥α,则b∥α;②若a∥α,α⊥β,则a⊥β;③若a⊥β,α⊥β,则a∥α;④若a⊥b,a⊥α,b⊥β,则α⊥β.7.空间四边形中,是中点,为中点,过的平面与,分别相交于点,,求证:平面.第3页共4页人的大脑和肢体一样,多用则灵,不用则废!8.如图,AB为⊙O的直径,C为⊙O上的一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F.求证:面ABD⊥平面AEF.9.如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC.(1)求三棱锥D-ABC的表面积;(2)求证:AC⊥平面DEF;(3)若M为BD中点,问AC上是否存在一点N,使MN∥平面DEF?若存在,说明点N的位置;若不存在,试说明理由.第4页共4页ECBDAFNM