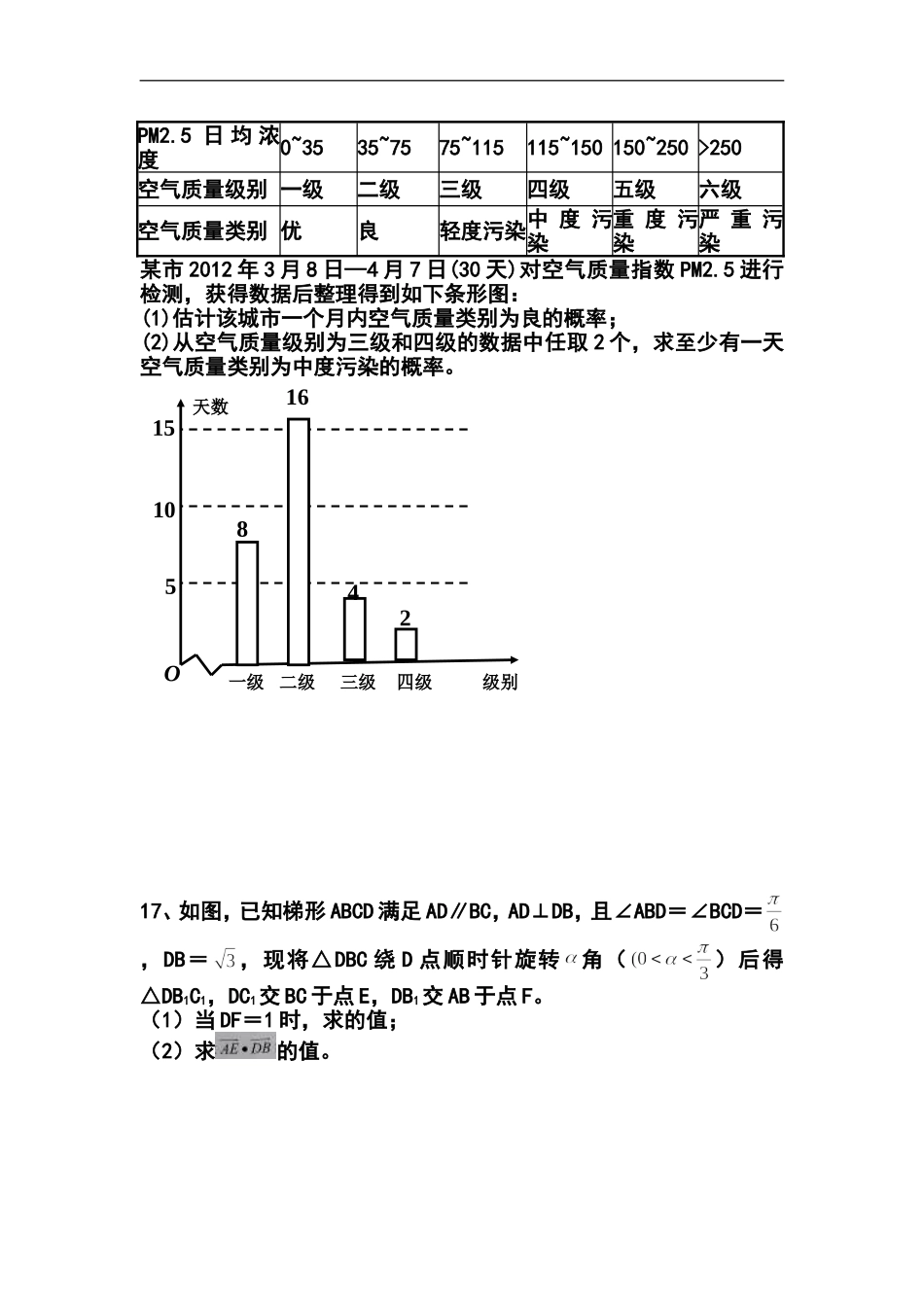
广东省佛山市2013届高三4月教学质量检测(二)文科数学一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。1、复数z满足,则z=2、集合,定义集合已知,则的子集为3、设函数若f(x)为奇函数,则g(-4)的值是A、-2B、-C、-D、24、已知非零向量的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5、已知a,b是两条不重合的直线,是两个不重合的平面,下列命题中正确的是()6、若,则m+3n的最小值等于()7.随机抽取某花场甲,乙两种计划在植树节期间移种的树苗各10株,测量它们的高度(单位:cm),获得高度数据的茎叶图如图,则下列关于甲、乙两种各10株树苗高度的结论正确的是()FAEDBCA.甲种树苗高度的方差较大B.甲种树苗高度的平均值较大C.甲种树苗高度的中位数较大D.甲种树苗高度在175以上的株数较多8、设等差数列{}的前n项和是,且,那么下列不等式中不成立的是二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。(二)选做题(14、15题,考生只能从中选做一题,两题全答的,只计前一题的得分)14.(坐标系与参数方程选做题)在极坐标系中,射线03与曲线1C:4sin的异于极点的交点为A,与曲线2C:8sin的异于极点的交点为B,则||AB________.15.(几何证明选做题)如图,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且2DFCF,:::4:2:1AFFBBE,若CE与圆相切,则线段CE的长为.三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤。16.空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,解代表空气污染越严重:PM2.5日均浓度0~3535~7575~115115~150150~250>250空气质量级别一级二级三级四级五级六级空气质量类别优良轻度污染中度污染重度污染严重污染某市2012年3月8日—4月7日(30天)对空气质量指数PM2.5进行检测,获得数据后整理得到如下条形图:(1)估计该城市一个月内空气质量类别为良的概率;(2)从空气质量级别为三级和四级的数据中任取2个,求至少有一天空气质量类别为中度污染的概率。17、如图,已知梯形ABCD满足AD∥BC,AD⊥DB,且∠ABD=∠BCD=,DB=,现将△DBC绕D点顺时针旋转角()后得△DB1C1,DC1交BC于点E,DB1交AB于点F。(1)当DF=1时,求的值;(2)求的值。一级二级三级四级级别天数10155O81642一级二级三级四级级别天数10155O8164218、如图所示四棱锥PABCD中,PA底面ABCD,四边形ABCD中,ABAD,//BCAD,2PAABBC,4AD,E为PD的中点,F为PC中点.(1)求四棱锥P-ABCD的体积;(2)求证:CD平面PAC;(3)在棱PC上是否存在点M(异于点C),使得BM∥平面PAD,若存在,求的值,若不存在,说明理由。;20、已知椭圆E:222210xyabab的一个交点为13,0F,而且过点13,2H.(Ⅰ)求椭圆E的方程;.xy1A2ATGPMON(Ⅱ)设椭圆E的上下顶点分别为12,AA,P是椭圆上异于12,AA的任一点,直线12,PAPA分别交x轴于点,NM,若直线OT与过点,MN的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.2012年佛山市普通高中高三教学质量检测(二)数学(文科)答案一、选择题:BDAACCABCD二、填空题11e1213114231572三、解答题161718]19答:当售价为9元时,最大年利润为135万元。20GMNO1ATyx2AP(2),,OGGTGM连接1212003(0,1),(0,1),(2cos,sin)(02,)22(,0),(,0),(,)AAPttttMxNxGxy则设且1222:1,2cossin1,2cos1sinxANyxPttxtxt直线将点坐标代入,得:即12cos1sintxt同理可得:GMNO1ATyx2AP1202cos2cos221sin1sincosxxttxttt22222OTOGGTOGMG222200222422cos44sin4coscos1sincoscosttyyttttt22OTOT即线段的长为定值22*0121.:1(0,),0,2,.(1){}nnnnnnCxyPAadaadnNa设曲线上的点到点的距离的最小值为若求数列的通项公式;22(1)(,),1Pxyxy解:设则222222()()122()22nnnnnPAxyayyaaay22,||,22nnnnnaayRyPAdd当时,取得...