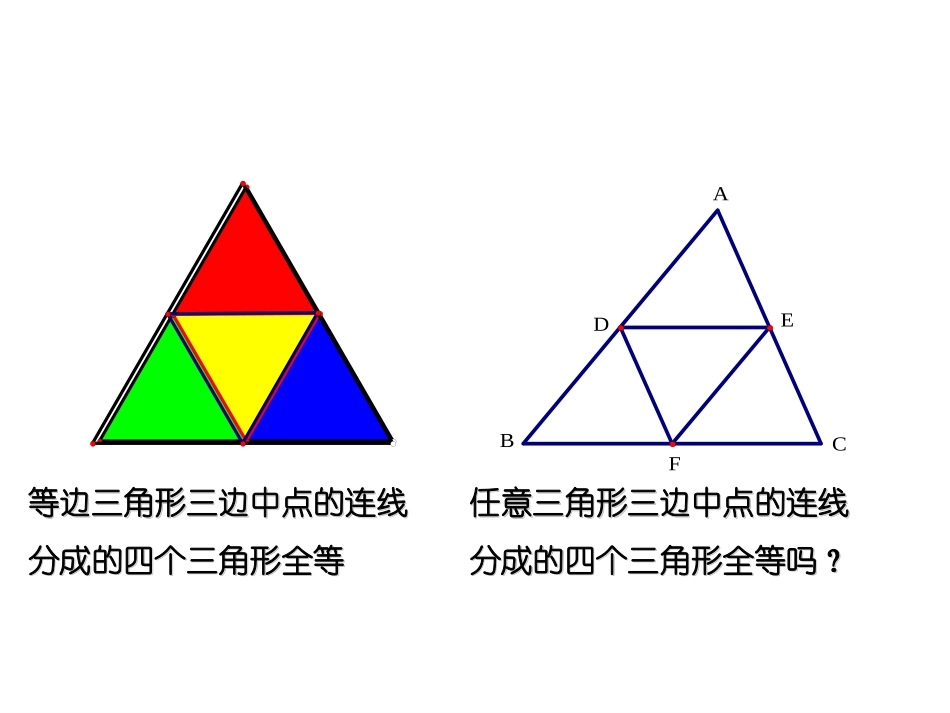
§36﹒三角形的中位线华师版九年级数学华师版九年级数学FEDCBA等边三角形三边中点的连线分成的四个三角形全等等边三角形三边中点的连线分成的四个三角形全等任意三角形三边中点的连线分成的四个三角形全等吗?任意三角形三边中点的连线分成的四个三角形全等吗?提纲导学•1、什么叫三角形的中位线?•2、三角形的中位线与三角形的中线有什么异同点?•3、三角形中位线定理的内容与证明方法•4、三角形中位线定理的应用图中线段DE是连接ΔABC两边中点D、E所得的线段三角形中位线的概念三角形中位线的概念连接三角形两边的中点的线段叫做三角形的中位线连接三角形两边的中点的线段叫做三角形的中位线三角形的中位线与三角形的中线的区别是什么?三角形的中位线与三角形的中线的区别是什么?三角形的中位线的两端都是边的中点;三角形的中线一端是边的中点,另一端是顶点.三角形的中位线的两端都是边的中点;三角形的中线一端是边的中点,另一端是顶点.EDCBA称此线段DE为ΔABC的中位线称此线段DE为ΔABC的中位线如图,DE是ΔABC的中位线,证明:DEBC∥。DE与BC之间存在什么样的数量关系呢?如图,DE是ΔABC的中位线,证明:DEBC∥。DE与BC之间存在什么样的数量关系呢?EDCBA此性质的特点:同一条件下有2个结论因为DE为ΔABC的中位线所以①DE∥BC,②DE=½BC↓↓位置关系数量关系EDCBA三角形的中位线平行于第三边,三角形的中位线平行于第三边,并且等于它的一半。并且等于它的一半。三角形中位线的性质:三角形中位线的性质:几何语言: DE是△ABC的中位线(或AD=BD,AE=CE)∴DE∥BC,且DE=1/2BC连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线因为D、E分别为AB、AC的中点所以DE为△ABC的中位线同理DF、EF也为△ABC的中位线EDFACB•例.求证三角形的一条中位线与第三边上的中线互相平分.FEDCBAFEDCBA已知:如图,在△ABC中,AD=DB,AE=EC,BF=FC求证:DE、AF互相平分已知:如图,在△ABC中,AD=DB,AE=EC,BF=FC求证:DE、AF互相平分证明:连结DF、EF AD=DB,BE=CE∴DEAC(∥三角形中位线定理)同理EFAB∥∴四边形ADEF是平行四边形∴DE、AF互相平分(平行四边形的对角线互相平分)证明:连结DF、EF AD=DB,BE=CE∴DEAC(∥三角形中位线定理)同理EFAB∥∴四边形ADEF是平行四边形∴DE、AF互相平分(平行四边形的对角线互相平分)拓展运用•猜一猜:画一个任意四边形,并画出四边的中点,再顺次连接四边形的中点,得到的四边形的形状是什么?说明理由.如图,四边形ABCD中,EFGH分别是ABCDADBC的中点,四边形EFGH是平行四边形吗?为什么?如图,四边形ABCD中,EFGH分别是ABCDADBC的中点,四边形EFGH是平行四边形吗?为什么?解:四边形EFGH是平行四边形解:四边形EFGH是平行四边形证明:连接DB证明:连接DB E、H分别是AB、AD的中点, E、H分别是AB、AD的中点,即EH是ΔABD的中位线即EH是ΔABD的中位线∴EH∥BD,EH=½BD,∴EH∥BD,EH=½BD,同理可得,FG∥BDFG=½BD同理可得,FG∥BDFG=½BD∴EH∥FG,EH=FG∴EH∥FG,EH=FG∴四边形EFGH是平行四边形.∴四边形EFGH是平行四边形.HGFEDCBA课堂训练1、如图(1)ΔABC中,AB=6㎝,AC=8㎝,BC=10㎝,D﹑E﹑F分别是ABACBC的中点则ΔDEF的周长是____,面积是____。2.如图(2)ΔABC中,DE是中位线,AF是中线,则DE与AF的关系是____2.如图(2)ΔABC中,DE是中位线,AF是中线,则DE与AF的关系是____3.若顺次连接四边形四边中点所得的四边形是菱形,则原四边形()(A)一定是矩形(B)一定是菱形(C)对角线一定互相垂直(D)对角线一定相等3.若顺次连接四边形四边中点所得的四边形是菱形,则原四边形()(A)一定是矩形(B)一定是菱形(C)对角线一定互相垂直(D)对角线一定相等FFAABBccDDEE(1)(1)AACCBBDDEEFF(2)(2)互相平分互相平分6cm26cm212cm12cmDDFPEDCBAFPEDCBA已知:四边形ABCD中,AB=CD,E、F分别是AD、BC的中点,P是AC中点,求证:△PEF是等腰三角形.已知:四边形ABCD中,AB=CD,E、F分别是AD、BC的中点,P是AC中点,求证:△PEF是等腰三角形.已知:四边形ABCD中,AB=CD,E、F分别是...