直线和抛物线VIP免费

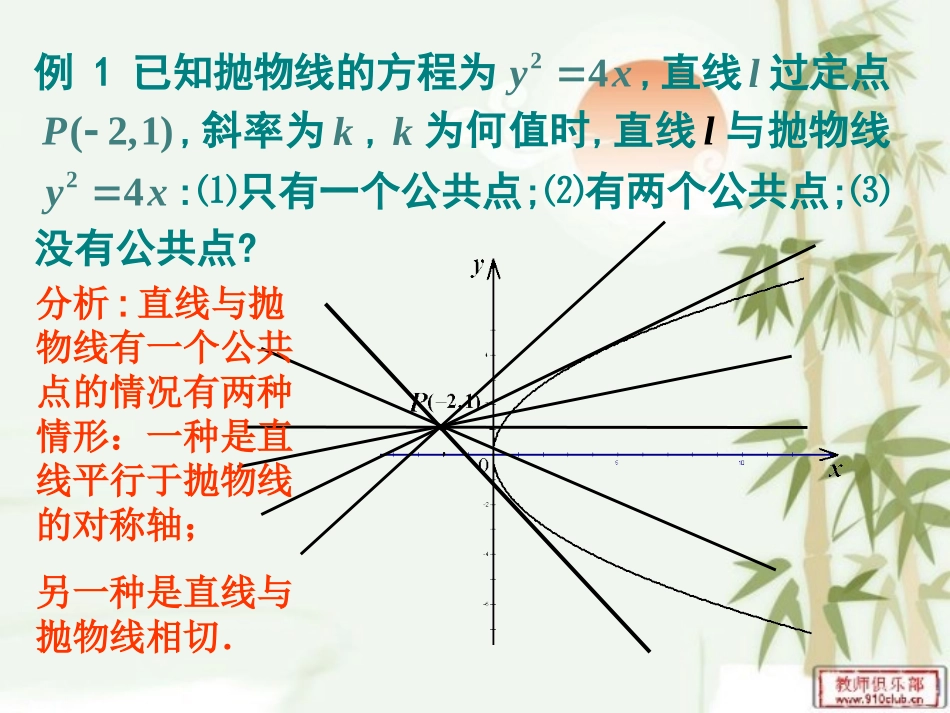
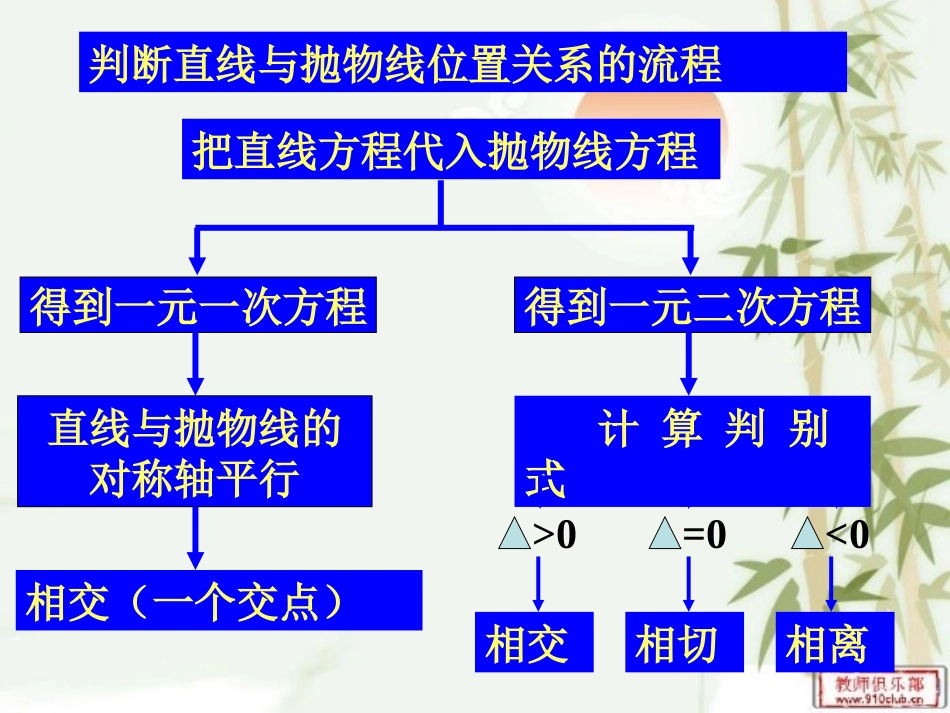
直线和抛物线例1已知抛物线的方程为24yx,直线l过定点(2,1)P,斜率为k,k为何值时,直线l与抛物线24yx:⑴只有一个公共点;⑵有两个公共点;⑶没有公共点?分析:直线与抛物线有一个公共点的情况有两种情形：一种是直线平行于抛物线的对称轴；另一种是直线与抛物线相切．判断直线与抛物线位置关系的流程把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线的对称轴平行相交（一个交点）计算判别式>0=0<0相交相切相离).2(1xkyl的方程为解：由题意，设直线xyxky4)2(12由方程组0)12(442kyky可得).12(160)2(2kkk＝时，方程的判别式为当0120120kk，即＝由.21,1kk或解得个公共点。即直线与抛物线只有一，时，方程组只有一个解，或即当211kk.10)1(yk时，由方程得当.41,412xxyy得代入把)1,41(点与抛物线只有一个公共这时，直线l0120220kk，即由.211k解得公共点。即直线与抛物线有两个时，方程组有两个解，且即当0,211kk0120320kk，即由.211kk，或解得共点。即直线与抛物线没有公，时，方程组没有实数解或即当211kk分析:直线与抛物线有两个公共点时△>0分析:直线与抛物线没有公共点时△<0个公共点。即直线与抛物线只有一时，，或，或综上所述，当0211kkk公共点。即直线与抛物线有两个时，且当0,211kk共点。即直线与抛物线没有公时，或当211kk注:在方程中,二次项系数含有k,所以要对k进行讨论作图要点:画出直线与抛物线只有一个公共点时的情形,观察直线绕点P转动的情形变式一:已知抛物线方程y2=4x,当b为何值时,直线l:y=x+b与抛物线(1)只有一个公共点(2)两个公共点(3)没有公共点.当直线与抛物线有公共点时,b的最大值是多少?分析:本题与例1类型相似,方法一样,通过联立方程组求得.(1)b=1(2)b<1(3)b>1,当直线与抛物线有公共点时,b的最大值当直线与抛物线相切时取得.其值为1变式二:已知实数x、y满足方程y2=4x,求函数的最值12yzx变式三:点(x,y)在抛物线y2=4x上运动,求函数z=x-y的最值.本题转化为过定点(-2,1)的直线与抛物线有公共点时斜率的最值问题.本题转化为直线y=x-z与抛物线有公共点时z的最值问题.min1z无最大值121minmaxkkOyxlPOyxABP的最大值求PABS的距离的最小值定直线到求抛物线上一动点lP知识迁移例2.过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.xOyFABDxyoFDBlA532.图.,,,.建立直角坐标系点它的顶点为原轴对称轴为以抛物线如图证明x532122,pxy设抛物线方程为2220020,,,xypyOAypyA的方程为线则直的坐标为点32.px抛物线的准线方程为43202.,ypyD点的纵坐标为可得、联立xyoFDBlA532.图.,,22202200ppypxyyAFpF的方程为直线所以的坐标是因为点52022.,ypyBpxy坐标为点的纵可得联立与.,//,平行于抛物线的对称轴故轴得、由DBxDB54?你还有其他证明方法吗•例3设A、B是抛物线y2＝2px(p＞0)上的两点，且OA⊥OB.(1)求A、B两点的横坐标之积和纵坐标之积；(2)求证：直线AB过定点；(3)求弦AB中点P的轨迹方程；(4)求ΔAOB面积的最小值．•AB过定点(2p,0)，设M(2p,0)．•当x1＝x2时，AB仍然过定点(2p,0)•∴中点P的轨迹方程为y2＝px-2p2.(p＞0)．•(4)SΔAOB＝SΔAOM＋SΔBOM＝|OM|(|y1|＋|y2|)＝p(|y1|＋|y2|)≥2p＝4p2，当且仅当|y1|＝|y2|＝2p时，等号成立，故ΔAOB面积的最小值为4p2..022正三角形的边长）上，求这个（两个顶点在抛物线点位于坐标原点，另外例、正三角形的一个顶ppxyyOxBA练习：.||||.0200.02022||||.222121212121212221222221212221212211轴对称关于，即线段由此可得，，，））（（，即：，，所以：又，），则，）、（，线上，且坐标分别为（在抛物、的顶点解：如图，设正三角形xAByyxxpxxpxxxxpxpxxxyxyxOBOApxypxyyxyxBAOAB.342||.322.3330tan301121111pyABpypyxxyAOxA...