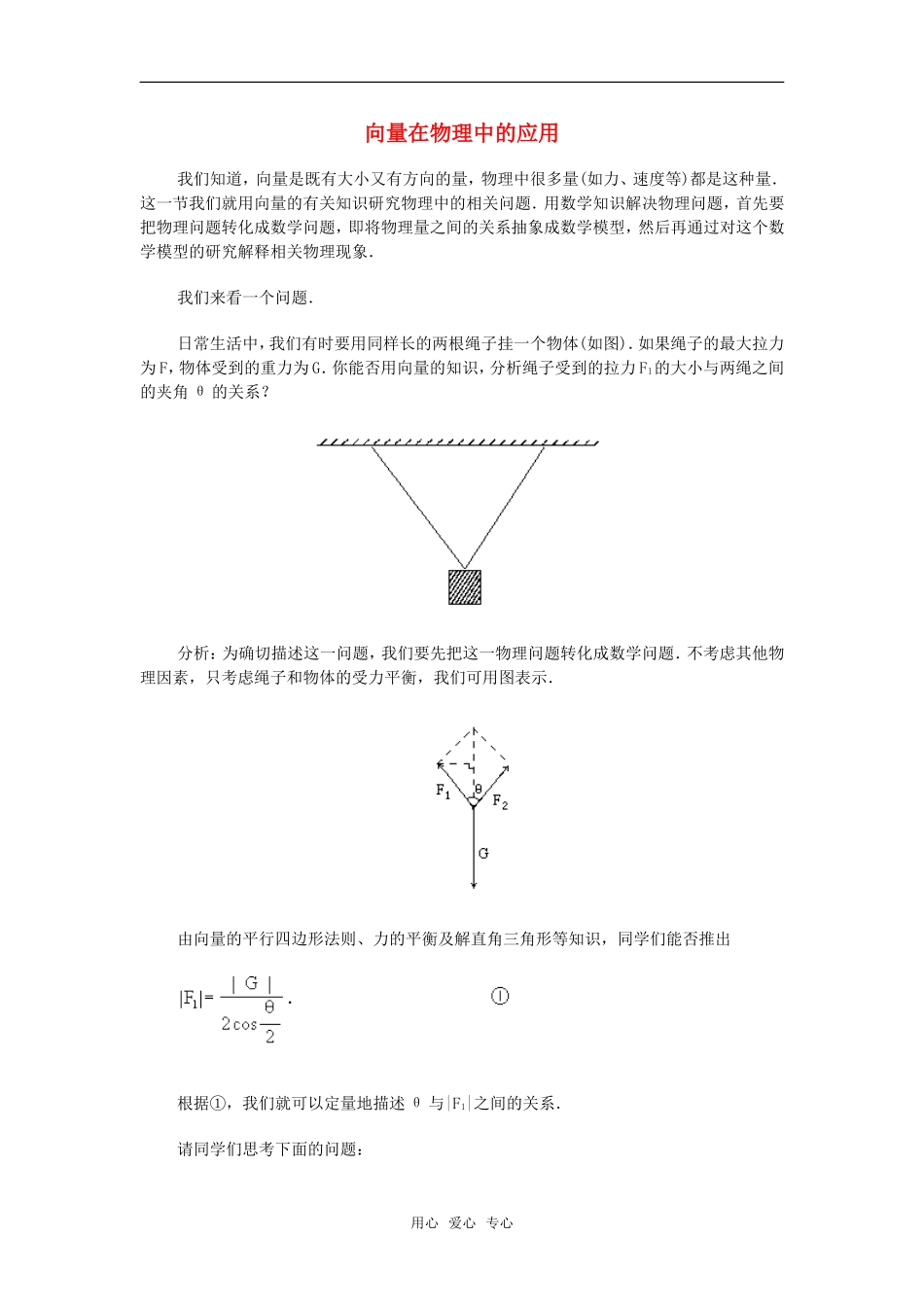
向量在物理中的应用我们知道,向量是既有大小又有方向的量,物理中很多量(如力、速度等)都是这种量.这一节我们就用向量的有关知识研究物理中的相关问题.用数学知识解决物理问题,首先要把物理问题转化成数学问题,即将物理量之间的关系抽象成数学模型,然后再通过对这个数学模型的研究解释相关物理现象.我们来看一个问题.日常生活中,我们有时要用同样长的两根绳子挂一个物体(如图).如果绳子的最大拉力为F,物体受到的重力为G.你能否用向量的知识,分析绳子受到的拉力F1的大小与两绳之间的夹角θ的关系?分析:为确切描述这一问题,我们要先把这一物理问题转化成数学问题.不考虑其他物理因素,只考虑绳子和物体的受力平衡,我们可用图表示.由向量的平行四边形法则、力的平衡及解直角三角形等知识,同学们能否推出根据①,我们就可以定量地描述θ与|F1|之间的关系.请同学们思考下面的问题:用心爱心专心1.当θ逐渐增大时,|F1|的大小怎样变化,为什么?2.θ为何值时,|F1|最小,最小值是多少?3.θ为何值时,|F1|=|G|?4.如果|F|=588N,|G|=882N,θ在什么范围时,绳子才不会断?5.请同学们自行设定|F|与|G|的大小,研究|F1|与θ的关系.1.因余弦函数在[0,π]之上是减函数,当θ增大时,|F1|也增大.3.θ=120°时,|F1|=|G|.4.0°≤θ<82°.根据①,我们还可以解释很多类似的物理现象.如“两个人共提一桶水,或者共提一个旅行包,夹角越大就越费力”,“在单杠上做引体向上,两臂的夹角越小就越省力”等.请同学们想一想,在你日常生活中,是否也有类似的物理现象,并用向量知识加以解释.我们再来看一个问题.如图,一条河的两岸平行,河的宽度d=500m.一艘船从A处出发航行到河的正对岸B处.船航行的速度|v1|=10km/h,水流速度|v2|=4km/h.那么v1与v2的夹角θ(精确到1°)多大时,船才能垂直到达对岸B处?船行驶多少时间(精确到0.1min)?分析:如果水是静止的,则船只要取垂直于河岸的方向行驶就行了.由于水流动的作用,船要被水冲向下游,因此要使船垂直到达对岸,就要使v1与v2的合速度的方向正好垂直于河岸方向(如图).用心爱心专心根据向量的平行四边形法则和解直角三角形的知识,可以算出:|v|=9.2km/h,θ=114°,t=3.3min.请同学们思考下面的两个问题.1.假设BC=BD=500m,要使船分别到达C处和D处,v1与v2的夹角θ分别是多少?分别行驶多少时间(精确到0.1min)?请同学们结合图,分别算出|v|、θ、t的值并填表1.出图形,分别计算出相应的|v|、θ、t的值并填表1.用心爱心专心2.当船垂直到达对岸时,所用时间最少吗?你能否推导出一个关于θ与t的关系式并加以说明.请同学们通过讨论解决这一问题.用向量还可以解决许多其他物理问题,你能找出一些问题并加以解决吗?用心爱心专心