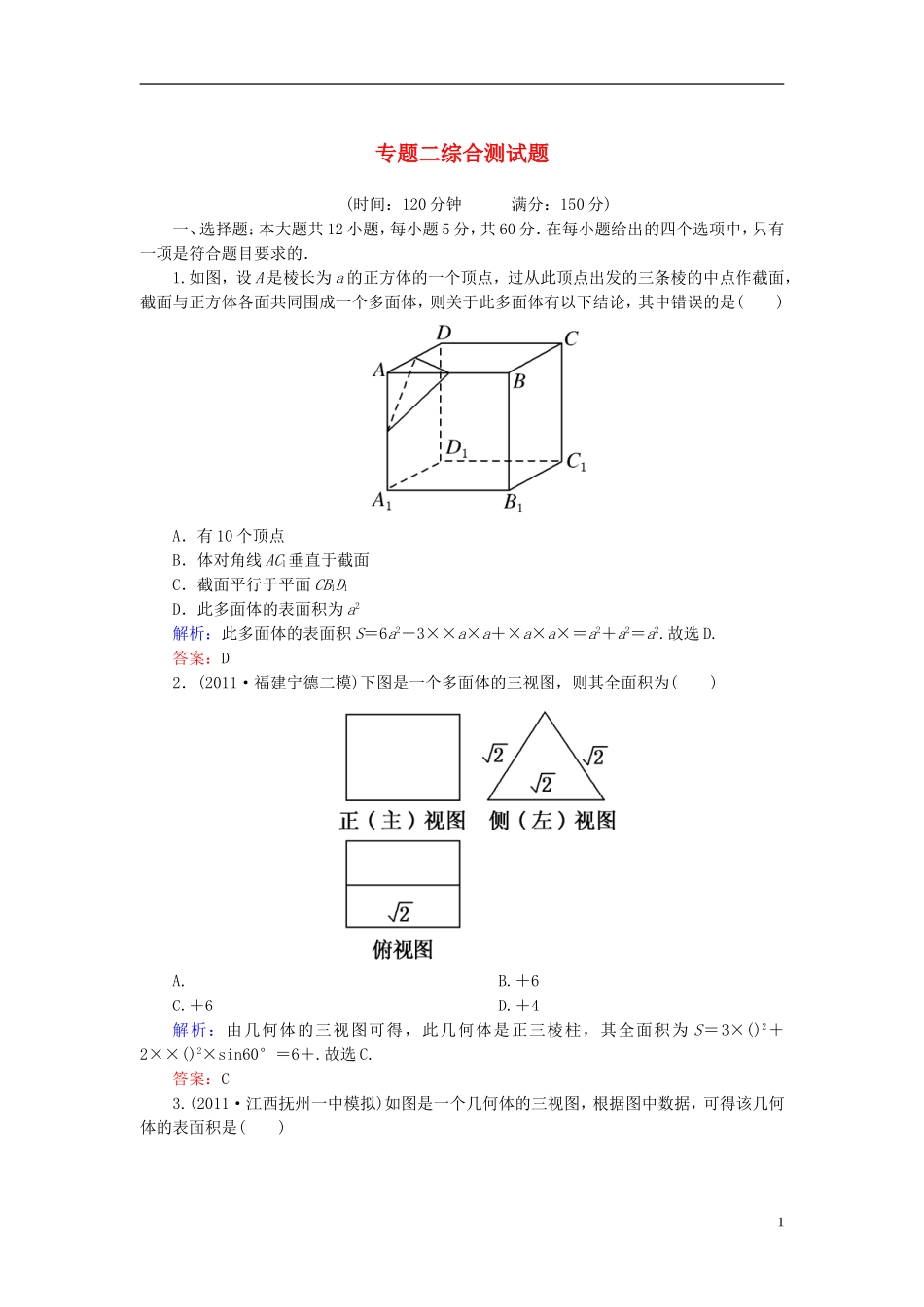
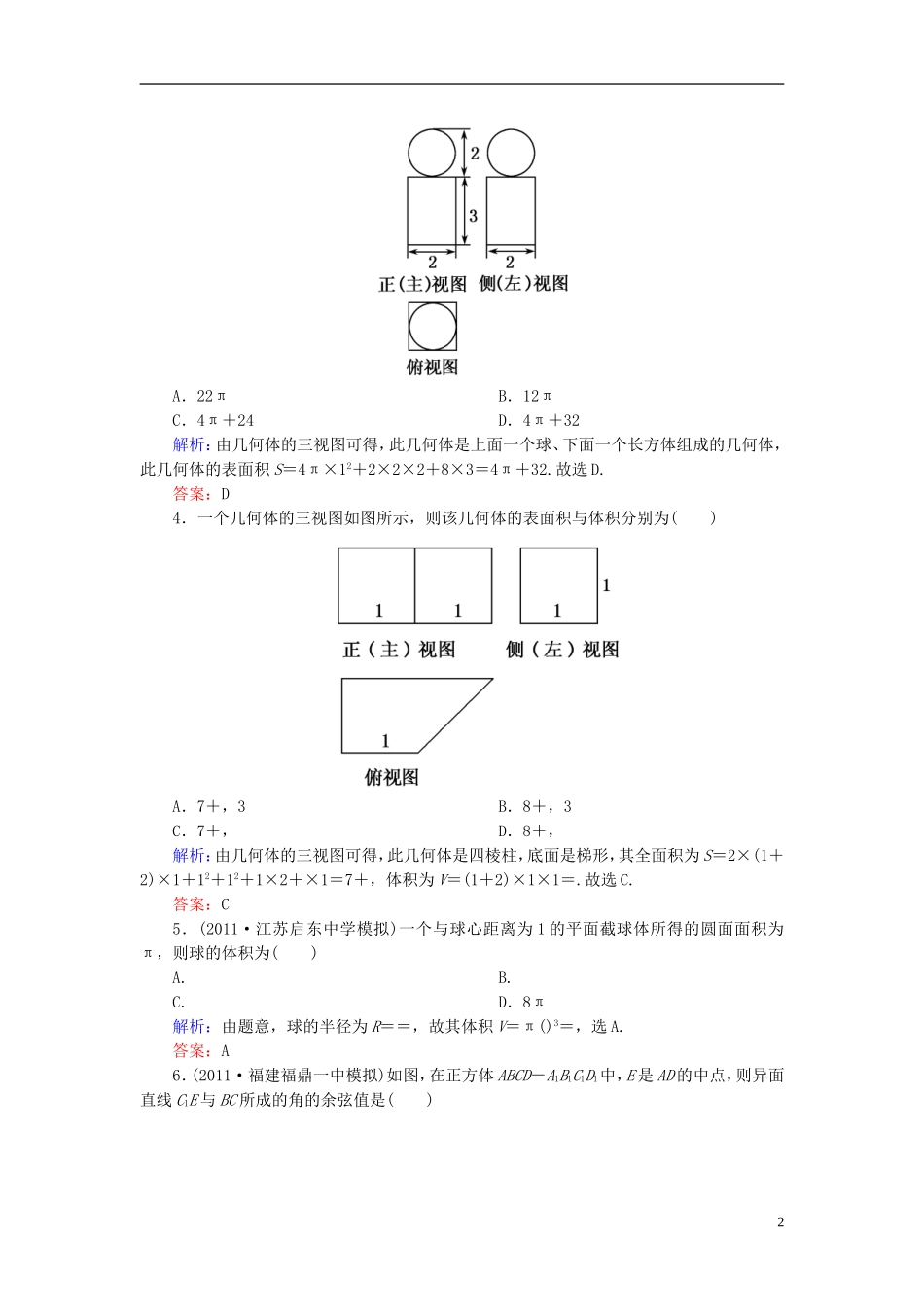
专题二综合测试题(时间:120分钟满分:150分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是()A.有10个顶点B.体对角线AC1垂直于截面C.截面平行于平面CB1D1D.此多面体的表面积为a2解析:此多面体的表面积S=6a2-3××a×a+×a×a×=a2+a2=a2.故选D.答案:D2.(2011·福建宁德二模)下图是一个多面体的三视图,则其全面积为()A.B.+6C.+6D.+4解析:由几何体的三视图可得,此几何体是正三棱柱,其全面积为S=3×()2+2××()2×sin60°=6+.故选C.答案:C3.(2011·江西抚州一中模拟)如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()1A.22πB.12πC.4π+24D.4π+32解析:由几何体的三视图可得,此几何体是上面一个球、下面一个长方体组成的几何体,此几何体的表面积S=4π×12+2×2×2+8×3=4π+32.故选D.答案:D4.一个几何体的三视图如图所示,则该几何体的表面积与体积分别为()A.7+,3B.8+,3C.7+,D.8+,解析:由几何体的三视图可得,此几何体是四棱柱,底面是梯形,其全面积为S=2×(1+2)×1+12+12+1×2+×1=7+,体积为V=(1+2)×1×1=.故选C.答案:C5.(2011·江苏启东中学模拟)一个与球心距离为1的平面截球体所得的圆面面积为π,则球的体积为()A.B.C.D.8π解析:由题意,球的半径为R==,故其体积V=π()3=,选A.答案:A6.(2011·福建福鼎一中模拟)如图,在正方体ABCD-A1B1C1D1中,E是AD的中点,则异面直线C1E与BC所成的角的余弦值是()2A.B.C.D.解析:因为BC∥B1C1,故∠EC1B1即为异面直线C1E与BC所成的角,在△EB1C1中,由余弦定理可得结果,选C.答案:C7.(2011·泰安市高三质检)已知正四棱锥S-ABCD的侧棱长与底面边长都相等,E是SB的中点,则AE、SD所成角的余弦值为()A.B.C.D.解析:连接BD,取BD中点O,连接AO则OE∥SD.∠OEA即为AE与SD所成的角.令侧棱长为2,则OE=1,AO=,AE=因为AE2=AO2+OE2,所以△AOE是直角三角形,故cos∠AEO=.答案:C8.(2011·安徽皖南八校联考)设m,n是不同的直线,α、β、γ是不同的平面,有以下四个命题:①⇒β∥γ;②⇒m⊥β;③⇒α⊥β;④⇒m∥α.其中正确的命题是()A.①④B.②③C.①③D.②④解析:由定理可知①③正确,②中m与β的位置关系不确定,④中可能m⊂α.故选C.答案:C9.(2011·宁夏模拟)如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是()3A.动点A′在平面ABC上的射影在线段AF上B.恒有平面A′GF⊥平面BCEDC.三棱锥A′—FED的体积有最大值D.异面直线A′E与BD不可能垂直解析:由题意,DE⊥平面AGA′,A、B、C正确.故选D.答案:D10.(2011·南昌一模)在棱长为a的正方体ABCD-A1B1C1D1中,M为AB的中点,则点C到平面A1DM的距离为()A.aB.aC.aD.a解析:设点C到平面A1DM的距离为h,则由已知得DM=A1M==a,A1D=a,S△A1DM=×a×=a2,连接CM,S△CDM=a2,由VC-A1DM=VA1-CDM,得S△A1DM·h=S△CDM·a,a2·h=a2·a,所以h=a,即点C到平面A1DM的距离为a,选A.答案:A11.(2011·山东平邑一中模拟)设a,b,c是空间三条直线,α,β是空间两个平面,则下列命题中,逆命题不成立的是()A.当c⊥α时,若c⊥β,则α∥βB.当b⊂α时,若b⊥β,则α⊥βC.当b⊂α,且c是a在α内的射影时,若b⊥c,则a⊥bD.当b⊂α,且c⊄α时,若c∥α,则b∥c解析:写出逆命题,可知B中b与β不一定垂直.选B.答案:B12.(2011·山东潍坊模拟)某几何体的一条棱长为,在该几何体的正视图中,这条棱的投影是长为的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为()A.2B.2C.4D.2解析:结合长方体的对角线在三个面的投影来理解计算.如图设长方体的长,宽,高分别4为m,n,k,由题意得=,=⇒n=1,=a,=b,所以(a2-1)+(b2-1)=6...