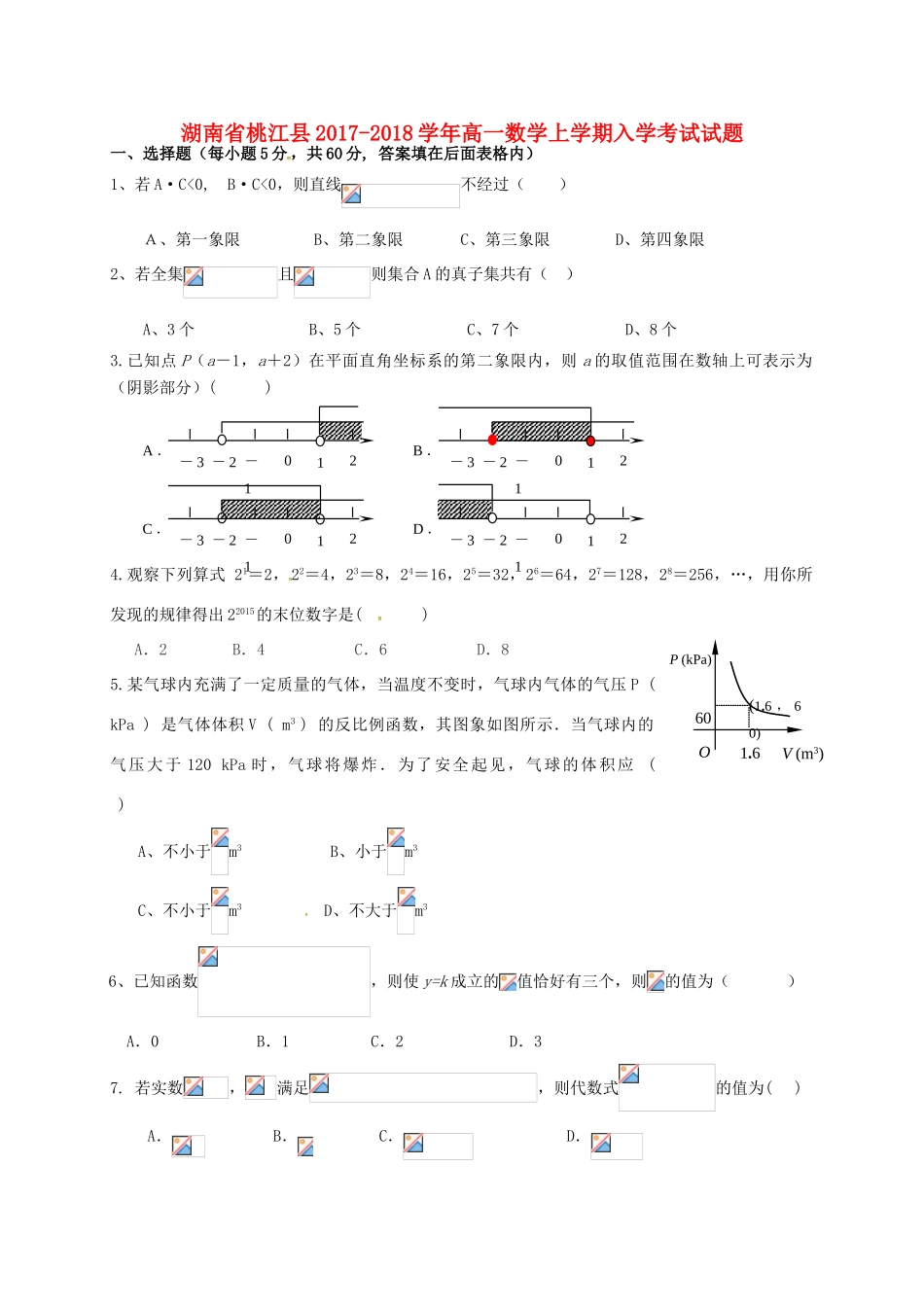
1.660OV(m3)P(kPa)(1.6,60)湖南省桃江县2017-2018学年高一数学上学期入学考试试题一、选择题(每小题5分,共60分,答案填在后面表格内)1、若A·C<0,B·C<0,则直线不经过()A、第一象限B、第二象限C、第三象限D、第四象限2、若全集且则集合A的真子集共有()A、3个B、5个C、7个D、8个3.已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为(阴影部分)()4.观察下列算式21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…,用你所发现的规律得出22015的末位数字是()A.2B.4C.6D.85.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于120kPa时,气球将爆炸.为了安全起见,气球的体积应()A、不小于m3B、小于m3C、不小于m3D、不大于m36、已知函数,则使y=k成立的值恰好有三个,则的值为()A.0B.1C.2D.37.若实数,满足,则代数式的值为()A.B.C.D.1-2-3-102A.1-2-3-102B.C.1-2-3-102D.1-2-3-1028.设计一个商标图案如图中阴影部分,矩形ABCD中,AB=2BC,且AB=8cm,以点A为圆心,AD为半径作圆与BA的延长线相交于点F,则商标图案的面积等于()A、(4π+8)cm2B、(4π+16)cm2C、(3π+8)cm2D、(3π+16)cm29.在平面直角坐标系中,OABC是正方形,点A的坐标是(4,0),点P为边AB上一点,∠CPB=60°,沿CP折叠正方形,折叠后,点B落在平面内点处,则点的坐标为()A、(2,)B、(,)C、(2,)D、(,)10.一个袋中装有1个红球,1个黄球和两个小立方体,两个球除了颜色外都相同,两个立方体中一个每一面都涂红,另一个每个面都涂黄,除此以外它们都相同,从袋中摸出一个球和一个立方体,下面说法中错误的是()A、所有可能出现的结果有四种B、摸出2个都是红的概率为1/4C、摸出2个都是黄的概率为1/4D、摸出一红一黄的概率也是1/411.如图所示,二次函数的图象经过点,且与轴交点的横坐标分别为,其中,,下列结论:①;②;③;④.其中正确的有()A、1个B、2个C、3个D、4个12.如图,AB是⊙O的弦,C是AB的三等分点,连结OC并延长交⊙O于点D。若OC=3,CD=2,则圆心O到弦AB的距离是()A.6B.9-C.D.25-3第11题图1-1-22xyO二、填空题(每小题5分,共20分,答案填在后面指定位置。)13.若代数式可化为,则的值是.14.比较大小:--(“>”,或“<”).15.求函数的定义域为16.已知关于x的方程x2+2kx+k2+k+3=0的两根分别是x1、x2,则(x1-1)2+(x2-1)2的最小值是。三、解答题(共70分,17题10分,其余各题12分)17.已知求代数式的值18.化简再求值:,其中,。19.利用函数的单调性求函数上的最大值20.已知R为全集,(1)求A,B,,;(2)求.21.已知二次函数,其中(1)若方程有两个实根,且方程有两个相等的根,求的解析式;(2)若的图象与x轴交于A(-3,0),B(m,0)两点,且当时,恒成立.求实数的取值范围.22.已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示,四个顶点的坐标分别为O(0,0),BByyOCOCTAxTAxA(10,0),B(8,),C(0,),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;(1)求∠OAB的度数,并求当点A′在线段AB上时,S关于t的函数关系式;(2)当纸片重叠部分的图形是四边形时,求t的取值范围;(3)S存在最大值吗?若存在,求出这个最大值,并求此时t的值;若不存在,请说明理由。一.选择题(本大题共12小题,每小题5分,共60分)二.填空题(本大题共4小题,每小题5分,共20分)13、514、<15、16、8三、解答题17.1819.20.解:(1)A=[-1,3),B=[2,3],,(2)=={x︳x<2或x≥3}21.解:(1)据题意,设①由方程②因为方程②有两个相等的根,所以,123456789101112CCCDCDAACDDC即(舍去)将代入①得的解析式(2)据题意知,是方程的两个根.由韦达定理故方程可化为要使得当时,恒成立.当且仅当故实数的取值范围为22.解:(1) A,B两点的坐标分别是A(10,0)和B(8,),∴,∴当点A´在线段AB上时, ...