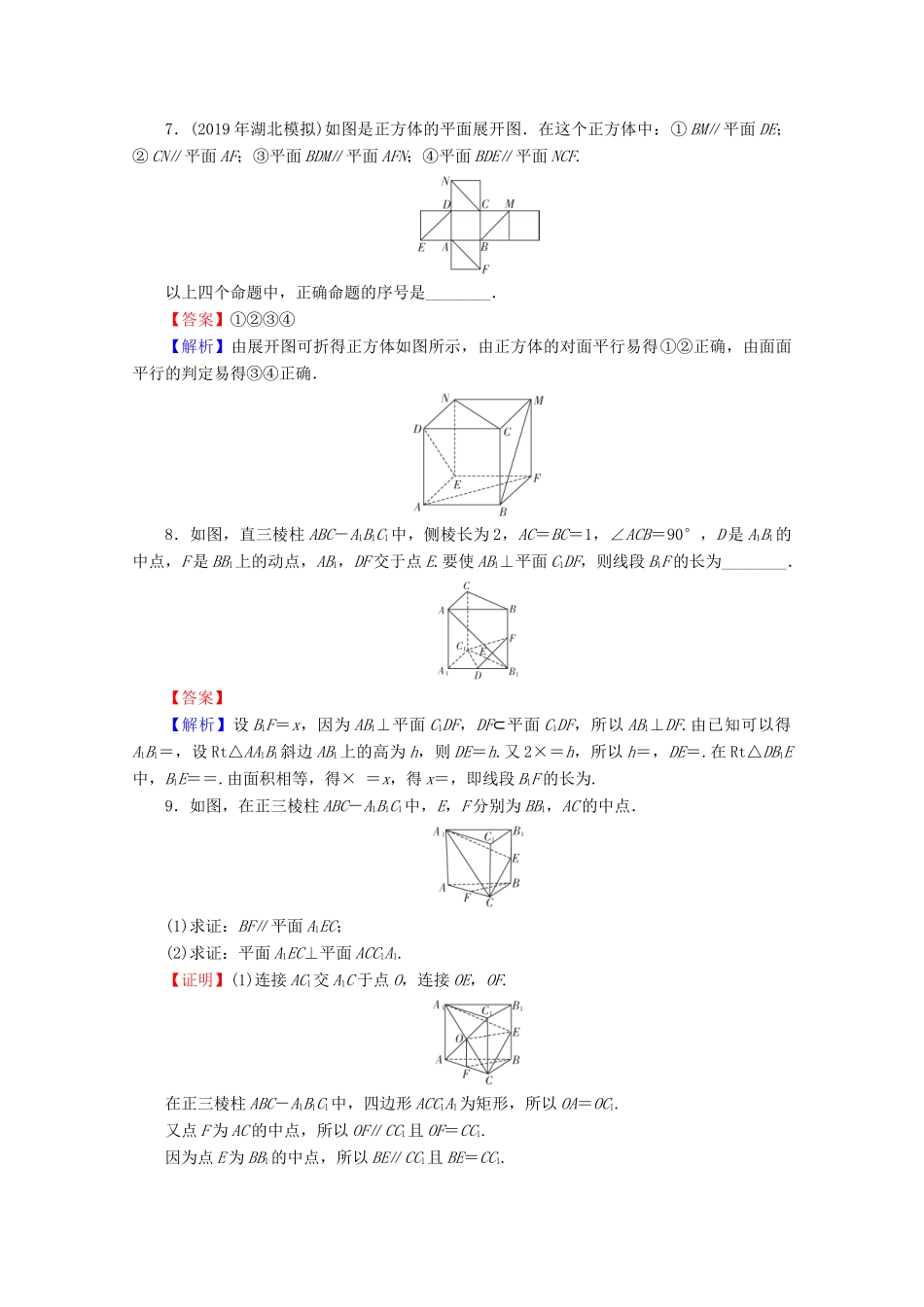
第2讲平行与垂直的判定与性质专题复习检测A卷1.△ABC所在的平面为α,直线l⊥AB,l⊥AC,直线m⊥BC,m⊥AC,则直线l,m的位置关系是()A.相交B.异面C.平行D.不确定【答案】C【解析】l⊥AB,l⊥AC⇒l⊥α;m⊥BC,m⊥AC⇒m⊥α.故l∥m.2.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是()A.若m⊥α,n⊥α,则m∥nB.若α⊥γ,β⊥γ,则α∥βC.若m∥α,n∥α,则m∥nD.若m∥α,m∥β,则α∥β【答案】A【解析】垂直于同一个平面的两条直线平行,A正确;α,β垂直于同一个平面γ,则α,β可能相交或平行,B错误;m,n平行于同一个平面,则m,n可能相交、平行或异面,C错误;α,β平行于同一条直线m,则α,β可能相交或平行,D错误.故选A.3.(2018年福建三明二模)如图,已知正方体ABCD-A1B1C1D1的棱长为2,则以下四个命题中错误的是()A.直线A1C1与AD1为异面直线B.A1C1∥平面ACD1C.BD1⊥ACD.三棱锥D1-ADC的体积为【答案】D【解析】A中,直线A1C1⊂平面A1B1C1D1,BD1⊄平面A1B1C1D1,D1∉直线A1C1,由异面直线判定定理得直线A1C1与AD1为异面直线,故A正确;B中, A1C1∥AC,A1C1⊄平面ACD1,AC⊂平面ACD1,∴A1C1∥平面ACD1,故B正确;C中,正方体ABCD-A1B1C1D1中,AC⊥BD,AC⊥DD1, BD∩DD1,∴AC⊥平面BDD1,∴BD1⊥AC,故C正确;D中,三棱锥D1-ADC的体积VD1-ADC=××2×2×2=,D错误.故选D.4.用a,b,c表示空间中三条不同的直线,γ表示平面,给出下列命题:①若a⊥b,b⊥c,则a∥c;②若a∥b,a∥c,则b∥c;③若a∥γ,b∥γ,则a∥b;④若a⊥γ,b⊥γ,则a∥b.其中真命题的序号是()A.①②B.②③C.①④D.②④【答案】D【解析】若a⊥b,b⊥c,则a∥c或a与c相交或a与c异面,所以①是假命题;在空间中,平行于同一直线的两条直线平行,所以②是真命题;若a∥γ,b∥γ,则a∥b或a与b相交或a与b异面,所以③是假命题;若两条直线垂直于同一个平面,则这两条直线平行,所以④是真命题.故选D.5.(2018年福建泉州模拟)如图,在下列四个正方体ABCD-A1B1C1D1中,E,F,G均为所在棱的中点,过E,F,G作正方体的截面,则在各个正方体中,直线BD1与平面EFG不垂直的是()ABCD【答案】B【解析】如图,在正方体中,E,F,G,M,N,Q均为所在棱的中点,EFMNQG是一个平面图形,直线BD1与平面EFMNQG垂直,且选项A,C,D中的平面与这个平面重合,满足题意,只有选项B中的直线BD1与平面EFG不垂直.故选B.6.(2019年北京)已知l,m是平面α外的两条不同直线.给出下列三个论断:①l⊥m;②m∥α;③l⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:________.【答案】若l⊥m,l⊥α,则m∥α(若m∥α,l⊥α,则l⊥m)【解析】从三个论断中选两个作为条件,余下的一个论断作为结论,共有三种可能.其中①③⇒②,②③⇒①是正确的命题,①②⇒③是错误的命题,故可填“若l⊥m,l⊥α,则m∥α”或“若m∥α,l⊥α,则l⊥m”.7.(2019年湖北模拟)如图是正方体的平面展开图.在这个正方体中:①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是________.【答案】①②③④【解析】由展开图可折得正方体如图所示,由正方体的对面平行易得①②正确,由面面平行的判定易得③④正确.8.如图,直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E.要使AB1⊥平面C1DF,则线段B1F的长为________.【答案】【解析】设B1F=x,因为AB1⊥平面C1DF,DF⊂平面C1DF,所以AB1⊥DF.由已知可以得A1B1=,设Rt△AA1B1斜边AB1上的高为h,则DE=h.又2×=h,所以h=,DE=.在Rt△DB1E中,B1E==.由面积相等,得×=x,得x=,即线段B1F的长为.9.如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.(1)求证:BF∥平面A1EC;(2)求证:平面A1EC⊥平面ACC1A1.【证明】(1)连接AC1交A1C于点O,连接OE,OF.在正三棱柱ABC-A1B1C1中,四边形ACC1A1为矩形,所以OA=OC1.又点F为AC的中点,所以OF∥CC1且OF=CC...