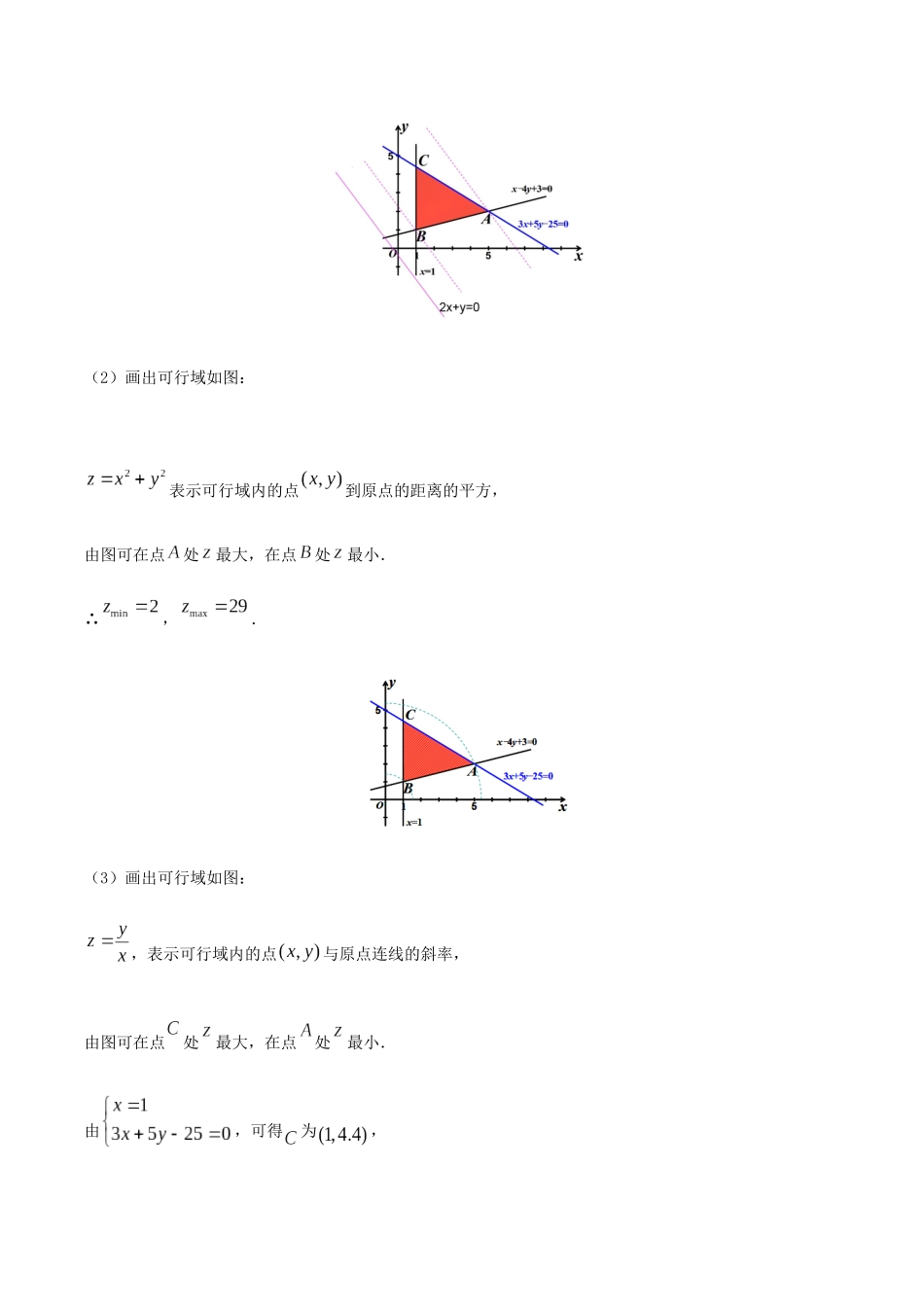
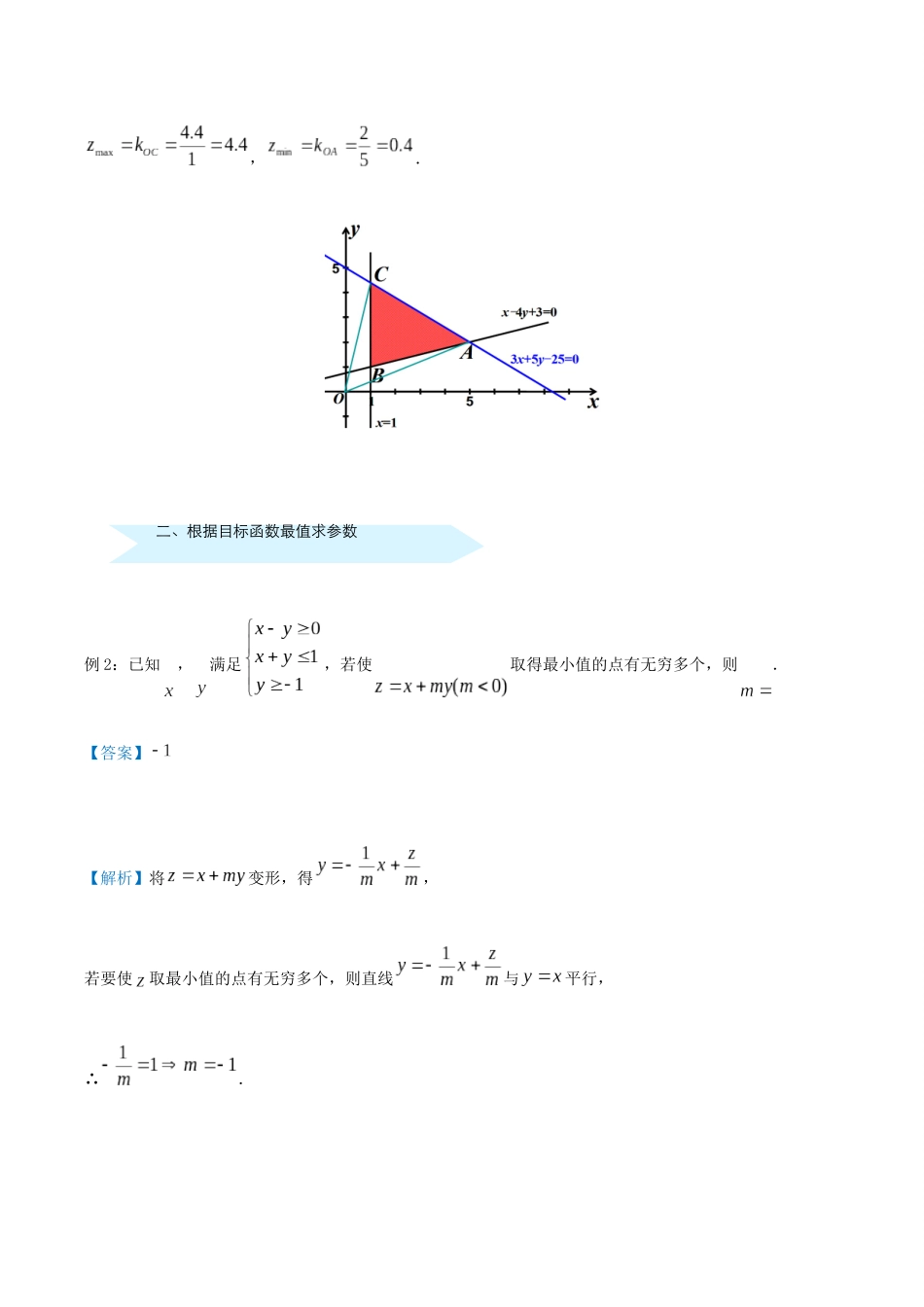
一、求目标函数的最值培优点九线性规划例1:已知、满足.(1)若,求的最值;(2)若,求的最值;(3)若,求的最值.【答案】(1),;(2),;(3),.【解析】(1)画出可行域如图:画出直线,并平移得在点处最大,在点处最小.由,求出为,由,求出为,,.(2)画出可行域如图:表示可行域内的点到原点的距离的平方,由图可在点处最大,在点处最小.∴,.(3)画出可行域如图:,表示可行域内的点与原点连线的斜率,由图可在点处最大,在点处最小.由,可得为,二、根据目标函数最值求参数,.例2:已知,满足,若使取得最小值的点有无穷多个,则.【答案】【解析】将变形,得,若要使取最小值的点有无穷多个,则直线与平行,∴.例3:已知不等式组,所表示的平面区域为面积等于的三角形,则实数的值为()A.B.C.D.【答案】D【解析】由已知得,不等式组,所表示的平面区域如图:yxy=x+2y=kx1123–112–1–2O三角形的一个顶点的坐标为.三、线性规划的应用 直线与轴的交点的坐标为,直线与的交点的坐标为,∴,即,∴三角形的面积为,解得(舍去).故选D.例4:某校食堂以面食和米食为主,面食每百克含蛋白质个单位,含淀粉个单位,售价元;米食每百克含蛋白质个单位,含淀粉个单位,售价元.学校要给学生配制成盒饭,每盒至少有个单位的蛋白质和个单位的淀粉,应如何配制盒饭,才既科学又使费用最少?【答案】每份盒饭中有面食百克,米食为百克,费用最省.【解析】设每份盒饭中面食为百克,米食为百克,费用元.对点增分集训目标函数为,线性约束条件为,画出可行域如图:画出直线并平移,得在点处最小,求出点为.所以每份盒饭中有面食百克,米食为百克,费用最省.一、选择题1.已知点和在直线的两侧,则实数的取值范围为()A.B.C.D.【答案】A【解析】由题意可知,所以,所以.2.已知,满足,则的最小值为()A.B.C.D.【答案】B【解析】作出不等式组,表示的区域如图,yxAx-y=0x=4x+y-4=012345–11234–1O结合图形可知当动直线经过点时,动直线在轴的截距最大,有最小值,.3.已知满足,则的最大值等于()A.B.C.D.【答案】C【解析】作出约束条件所表示的平面区域(如图),而,表示点和的连线的斜率,由图知点和连线的斜率最大,所以.4.不等式组表示的平面区域的面积为()A.B.C.D.【答案】A【解析】作出约束条件所表示的平面区域(如图),,,所以三角形面积为.yx2x-y-6=0x+y-3=0y=2CBA123123–1O5.已知,,满足约束条件,若的最小值为,()A.B.C.D.【答案】B【解析】如图所示,画出可行域(如图内部),目标函数可化为,当直线经过时取到最小值,则,即.yxDCB123123–1O6.设实数,满足约束条件,则的最大值为()A.B.C.D.【答案】D【解析】由实数,满足约束条件,作可行域如图,yxBA1234123456O由图可知,当过时,取得最大值,由,解得,此时取最大值.7.已知实数,满足不等式组,若目标函数的最大值为,则的值为()A.B.C.D.【答案】D【解析】不等式的可行域,如图所示,yxx-y+2=0x+y-4=02x-y-5=0CBA12345678–1123456789–1O令,则可得,当最大时,直线的纵截距最大,将直线平移可知,目标函数经过点时,取最大值,可得,∴.8.实数,满足条件,目标函数的最小值为,则该目标函数的最大值为()A.B.C.D.【答案】D【解析】画出满足条件的可行域,可知目标函数在点处取得最小值,所以,求得,从而目标函数在点处取得最大值,即.yxA1234–11234–1–2O二、填空题9.设,满足约束条件,求的最大值.【答案】【解析】可行域如图所示中的区域,yxCBA123456–112345O得,,,作出直线,再将直线平移,当经过点时,轴截距最大,即达到最大值,得,所以最大值是.10.不等式组表示的平面区域的面积为.【答案】【解析】不等式组所表示的平面区域如图中阴影部分,易求得,点坐标,,∴.yxDx+2y-4=0x+y-2=0x+3y-2=0CBAO11.某农户计划种植黄瓜和韭菜,种植面积不超过亩,投入资金不超过万元,假设种植黄瓜和韭菜的产量;成本和售价如下表:为使一年的种植总利润(总利润总销售收入总种植成本)最大,那么黄瓜的种植面积...