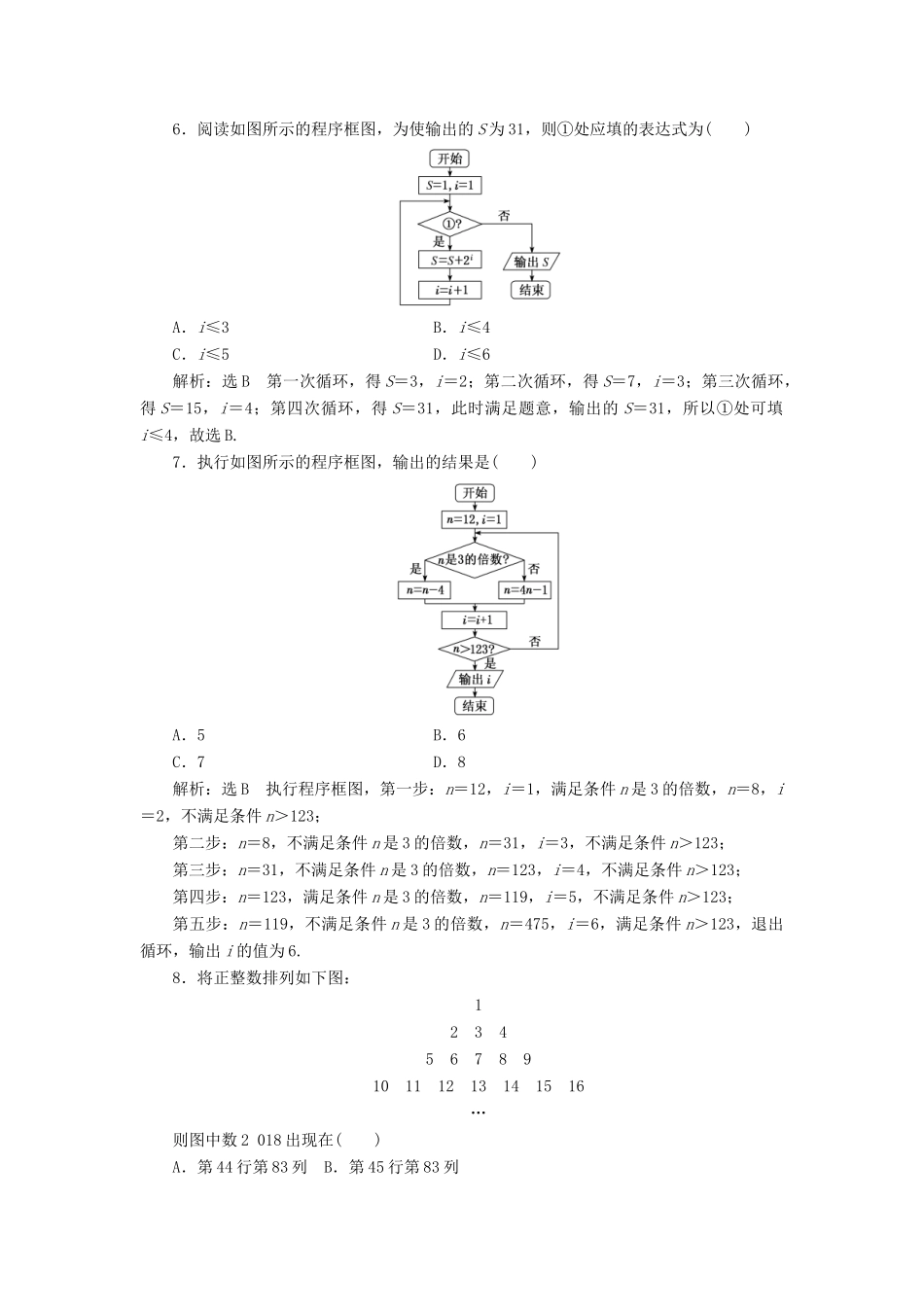
寒假作业(二十一)算法、复数、推理与证明(注意速度和准度)一、“12+4”提速练1.设z=1+i(i是虚数单位),则-=()A.iB.2-iC.1-iD.0解析:选D因为-=-1+i=-1+i=1-i-1+i=0,故选D.2.已知复数z=(a∈R),且z的实部与虚部相等,则z的共轭复数=()A.+iB.-iC.1+iD.1-i解析:选Bz====-i,因为z的实部与虚部相等,所以z=+i,则z的共轭复数=-i.3.在复平面内与复数z=所对应的点关于实轴对称的点为A,则A对应的复数为()A.1+iB.1-iC.-1-iD.-1+i解析:选B因为z===i(1-i)=1+i,所以A点坐标为(1,-1),其对应的复数为1-i,故选B.4.(2017·北京高考)执行如图所示的程序框图,输出的s值为()A.2B.C.D.解析:选C运行该程序,k=0,s=1,k<3;k=0+1=1,s==2,k<3;k=1+1=2,s==,k<3;k=1+2=3,s==,此时不满足循环条件,输出s,故输出的s值为.5.若z=(a-)+ai为纯虚数,其中a∈R,则=()A.iB.1C.-iD.-1解析:选C z为纯虚数,a∈R,∴a=,∴====-i.6.阅读如图所示的程序框图,为使输出的S为31,则①处应填的表达式为()A.i≤3B.i≤4C.i≤5D.i≤6解析:选B第一次循环,得S=3,i=2;第二次循环,得S=7,i=3;第三次循环,得S=15,i=4;第四次循环,得S=31,此时满足题意,输出的S=31,所以①处可填i≤4,故选B.7.执行如图所示的程序框图,输出的结果是()A.5B.6C.7D.8解析:选B执行程序框图,第一步:n=12,i=1,满足条件n是3的倍数,n=8,i=2,不满足条件n>123;第二步:n=8,不满足条件n是3的倍数,n=31,i=3,不满足条件n>123;第三步:n=31,不满足条件n是3的倍数,n=123,i=4,不满足条件n>123;第四步:n=123,满足条件n是3的倍数,n=119,i=5,不满足条件n>123;第五步:n=119,不满足条件n是3的倍数,n=475,i=6,满足条件n>123,退出循环,输出i的值为6.8.将正整数排列如下图:12345678910111213141516…则图中数2018出现在()A.第44行第83列B.第45行第83列C.第44行第82列D.第45行第82列解析:选D由题意可知第n行有2n-1个数,则前n行的数的个数为1+3+5+…+(2n-1)=n2,因为442=1936,452=2025,且1936<2018<2025,所以2018在第45行,又2018-1936=82,故2018在第45行第82列.9.(2017·洛阳统考)某程序框图如图所示,该程序运行结束时输出的S值是()A.1007B.3026C.2016D.3024解析:选B依题意,在数列{an}中,an=nsin+1,a4n-3+a4n-2+a4n-1+a4n=[(4n-3)+1]+(0+1)+[-(4n-1)+1]+(0+1)=2,注意到2017=4×504+1,所以数列{an}的前2017项和等于504(a1+a2+a3+a4)+a2017=504×2+2018=3026.10.(2018届高三·惠州调研)执行如图所示的程序框图,则输出的结果为()A.7B.9C.10D.11解析:选B法一:第一步:i=1,S=lg=-lg3>-1;第二步:i=3,S=lg+lg=lg=-lg5>-1;第三步:i=5,S=lg+lg=lg=-lg7>-1;第四步:i=7,S=lg+lg=lg=-lg9>-1;第五步:i=9,S=lg+lg=lg=-lg11<-1,故输出的i=9.法二:因为S=lg+lg+…+lg=lg1-lg3+lg3-lg5+…+lgi-lg(i+2)=-lg(i+2),当i=9时,S=-lg(9+2)<-lg10=-1,所以输出的i=9.11.已知数列{an}是正项等差数列,若cn=,则数列{cn}也为等差数列.已知数列{bn}是正项等比数列,类比上述结论可得()A.若{dn}满足dn=,则{dn}也是等比数列B.若{dn}满足dn=,则{dn}也是等比数列C.若{dn}满足dn=(b1·2b2·3b3·…·nbn),则{dn}也是等比数列D.若{dn}满足dn=(b1·b·b·…·b),则{dn}也是等比数列解析:选D设等比数列{bn}的公比为q(q>0),则b1·b·b·…·b=b1·(b1q)2·(b1q2)3·…·(b1qn-1)n=(b1·b·b·…·b)(q1×2·q2×3·…·q(n-1)n)=b·q1×2+2×3+…+(n-1)n=b1q12+1+22+2+…+(n-1)2+(n-1)=b1q,所以dn=(b1·b·b·…·b)=b1q,即{dn}也是等比数列.12.埃及数学中有一个独特现象:除用一个单独的符号表示以外,其他分数都要写成若干个单位分数和的形式,例如=+.可以这样理解:假定有两个面包,要平均...