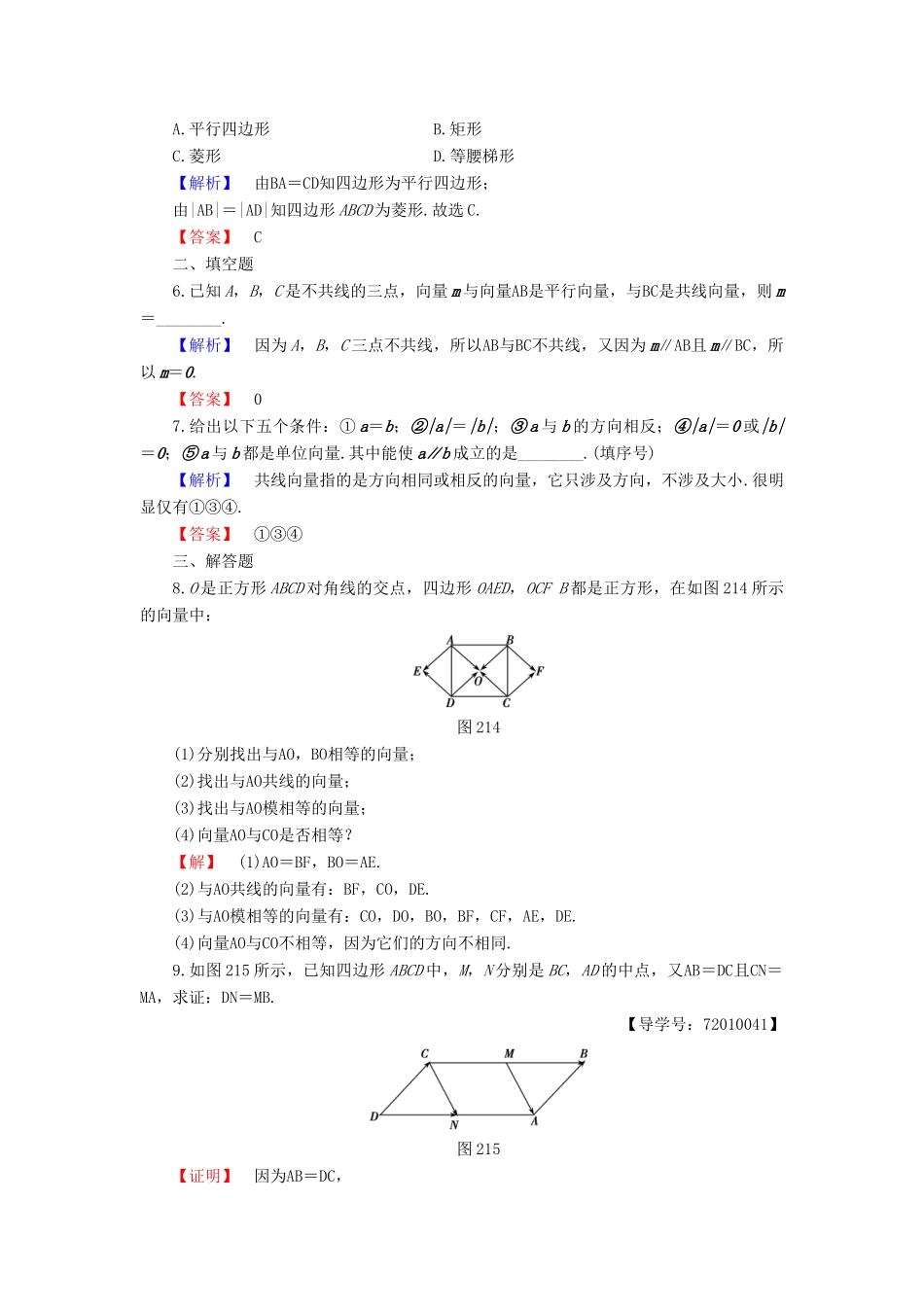
学业分层测评(十三)向量的概念(建议用时:45分钟)[学业达标]一、选择题1.下列说法正确的个数是()(1)温度、速度、位移、功这些物理量都是向量;(2)零向量没有方向;(3)非零向量的单位向量是唯一的.A.0B.1C.2D.3【解析】(1)中温度和功不是向量;(2)零向量的方向不确定,而不是没有方向,所以(1)(2)错误.【答案】B2.下列结论正确的是()A.向量必须用有向线段来表示B.表示一个向量的有向线段是唯一的C.有向线段AB和BA是同一向量D.有向线段AB和BA的大小相等【解析】向量除了可以用有向线段表示以外,还可用坐标或字母表示,所以选项A错误;向量为自由向量,只要大小相等,方向相同就为同一个向量,而与它的具体位置无关,所以表示一个向量的有向线段不是唯一的,选项B错误;有向线段AB和BA的方向相反,大小相等,不为同一向量,所以选项C错误,D正确.【答案】D3.给出下列四个命题:①若|a|=0,则a=0;②若|a|=|b|,则a=b或a=-b;③若a∥b,则|a|=|b|;④若a=0,则-a=0.其中正确的命题有()A.1个B.2个C.3个D.4个【解析】对于①,前一个零是实数,后一个应是向量0.对于②,两个向量的模相等,只能说明它们的长度相等,它们的方向并不确定.对于③,两个向量平行,它们的方向相同或相反,模未必相等.只有④正确.故选A.【答案】A4.数轴上点A,B分别对应-1、2,则向量AB的长度是()A.-1B.2C.1D.3【解析】易知|AB|=2-(-1)=3,故选D.【答案】D5.(2016·长春十一中期末)若|AB|=|AD|且BA=CD,则四边形ABCD的形状为()A.平行四边形B.矩形C.菱形D.等腰梯形【解析】由BA=CD知四边形为平行四边形;由|AB|=|AD|知四边形ABCD为菱形.故选C.【答案】C二、填空题6.已知A,B,C是不共线的三点,向量m与向量AB是平行向量,与BC是共线向量,则m=________.【解析】因为A,B,C三点不共线,所以AB与BC不共线,又因为m∥AB且m∥BC,所以m=0.【答案】07.给出以下五个条件:①a=b;②|a|=|b|;③a与b的方向相反;④|a|=0或|b|=0;⑤a与b都是单位向量.其中能使a∥b成立的是________.(填序号)【解析】共线向量指的是方向相同或相反的向量,它只涉及方向,不涉及大小.很明显仅有①③④.【答案】①③④三、解答题8.O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在如图214所示的向量中:图214(1)分别找出与AO,BO相等的向量;(2)找出与AO共线的向量;(3)找出与AO模相等的向量;(4)向量AO与CO是否相等?【解】(1)AO=BF,BO=AE.(2)与AO共线的向量有:BF,CO,DE.(3)与AO模相等的向量有:CO,DO,BO,BF,CF,AE,DE.(4)向量AO与CO不相等,因为它们的方向不相同.9.如图215所示,已知四边形ABCD中,M,N分别是BC,AD的中点,又AB=DC且CN=MA,求证:DN=MB.【导学号:72010041】图215【证明】因为AB=DC,所以|AB|=|DC|且AB∥DC,所以四边形ABCD是平行四边形,所以|DA|=|CB|且DA∥CB.又因为DA与CB的方向相同,所以CB=DA.同理可证,四边形CNAM是平行四边形,所以CM=NA.因为|CB|=|DA|,|CM|=|NA|,所以|MB|=|DN|.又DN与MB的方向相同,所以DN=MB.[能力提升]1.已知向量a,b是两个非零向量,AO,BO分别是与a,b同方向的单位向量,则以下各式正确的是()A.AO=BOB.AO=BO或AO=OBC.AO=OBD.AO与BO的长度相等【解析】因为a与b方向关系不确定且a≠0,b≠0,又AO与a同方向,BO与b同方向,所以AO与BO方向关系不确定,所以A,B,C均不对.又AO与BO均为单位向量,所以|AO|=|BO|=1.【答案】D2.已知飞机从A地按北偏东30°方向飞行2000km到达B地,再从B地按南偏东30°方向飞行2000km到达C地,再从C地按西南方向飞行1000km到达D地.画图表示向量AB,BC,CD,并指出向量AD的模和方向.【解】以A为原点,正东方向为x轴正方向,正北方向为y轴正方向建立直角坐标系.据题设,B点在第一象限,C点在x轴正半轴上,D点在第四象限,向量AB,BC,CD如图所示,由已知可得,△ABC为正三角形,所以AC=2000km.又∠ACD=45°,CD=1000km.所以△ADC为等腰直角三角形,所以AD=1000km,∠CAD=45°.故向量AD的模为1000km,方向为东南方向.