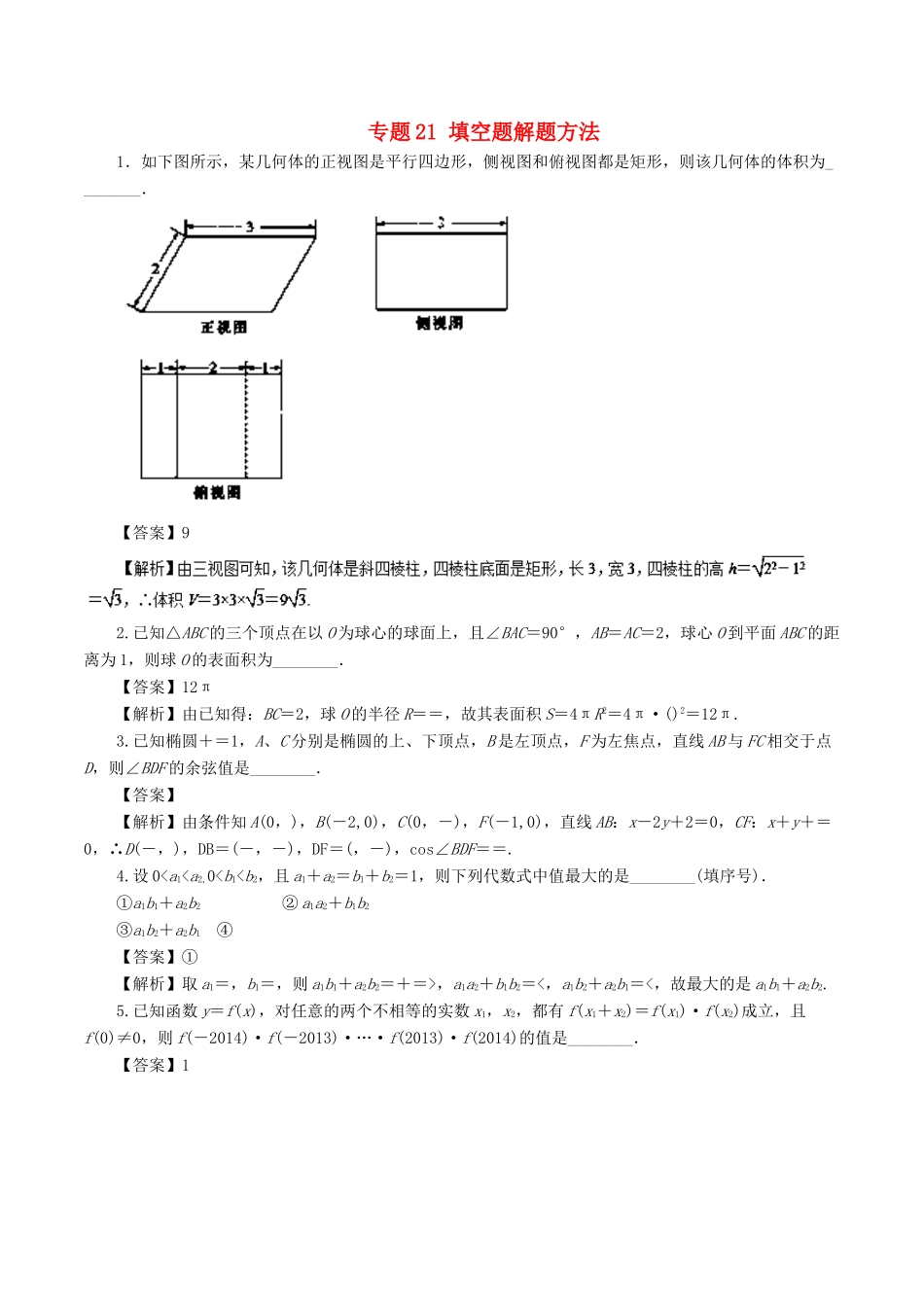
专题21填空题解题方法1.如下图所示,某几何体的正视图是平行四边形,侧视图和俯视图都是矩形,则该几何体的体积为________.【答案】92.已知△ABC的三个顶点在以O为球心的球面上,且∠BAC=90°,AB=AC=2,球心O到平面ABC的距离为1,则球O的表面积为________.【答案】12π【解析】由已知得:BC=2,球O的半径R==,故其表面积S=4πR2=4π·()2=12π.3.已知椭圆+=1,A、C分别是椭圆的上、下顶点,B是左顶点,F为左焦点,直线AB与FC相交于点D,则∠BDF的余弦值是________.【答案】【解析】由条件知A(0,),B(-2,0),C(0,-),F(-1,0),直线AB:x-2y+2=0,CF:x+y+=0,∴D(-,),DB=(-,-),DF=(,-),cos∠BDF==.4.设0
,a1a2+b1b2=<,a1b2+a2b1=<,故最大的是a1b1+a2b2.5.已知函数y=f(x),对任意的两个不相等的实数x1,x2,都有f(x1+x2)=f(x1)·f(x2)成立,且f(0)≠0,则f(-2014)·f(-2013)·…·f(2013)·f(2014)的值是________.【答案】16.△ABC的外接圆的圆心为O,两条边上的高相交于点H,若OH=m(OA+OB+OC),则实数m=________.【答案】1【解析】如图在Rt△ABC中,外接圆圆心O为斜边AB的中点,垂心H即为C点,由已知OH=m(OA+OB+OC)=mOC,则m=1.7.直线l1和l2是圆x2+y2=2的两条切线,若l1与l2的交点为(1,3),则l1与l2的夹角的正切值等于________.【答案】【解析】设l1、l2与⊙O分别相切于B、C,则∠OAB=∠OAC,|OA|=,圆半径为,∴|AB|==2,∴tan∠OAB==,∴所夹角的正切值tan∠CAB===.8.已知椭圆C:+=1,点M与C的焦点不重合.若M关于C的焦点的对称点分别为A、B,线段MN的中点在C上,则|AN|+|BN|=________.【答案】12【解析】如图.设MN与椭圆的交点为D,由中位线定理.|AN|+|BN|=2(|DF1|+|DF2|)由椭圆的定义知|DF1|+|DF2|=2a=6.∴|AN|+|BN|=12.9.向量OB=(1,0),OA=(+cosθ,1+sinθ),则OA与OB夹角的取值范围是________.【答案】[0,]【解析】依题意在坐标系中B(1,0)、A(+cosθ,1+sinθ),点A在圆(x-)2+(y-1)2=1的圆周上运动,如图,当A点为切点M时,OA与OB的夹角取最大值,容易求得为;当A点为切点N时,夹角取最小值0,故取值范围是[0,].10.不等式-kx+1≤0的解集非空,则k的取值范围为________.【答案】(-∞,-]∪[,+∞)由图可知A(-2,0),B(2,0),故kAC==-,kBC==.要使直线和半圆有公共点,则k≥或k≤-.所以k的取值范围为(-∞,-]∪[,+∞).11.△ABC的内角A,B,C的对边分别为a,b,c,已知ac=b2-a2,A=,则B=________.【答案】12.a=ln-,b=ln-,c=ln-,则a、b、c的大小关系为________.【答案】a>b>c【解析】令f(x)=lnx-x,则f′(x)=-1=.当00,即函数f(x)在(0,1)上是增函数. 1>>>>0,∴a>b>c.13.如图,已知球O的球面上有四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=,则球O的体积等于________.【答案】π【解析】如图,以DA、AB、BC为棱长构造正方体,设正方体的外接球球O的半径为R,则正方体的体对角线长即为球O的直径,所以|CD|==2R,所以R=,故球O的体积V==π.14.设(x-3)2+(y-3)2=6,则的最大值为________.【答案】3+2【解析】设=k,则可转化为直线kx-y=0与圆(x-3)2+(y-3)2=6有公共点时k的取值范围,用代数法(Δ≥0)或几何法(d≤r)解决.15.已知P(x,y)是椭圆+=1上的一个动点,则x+y的最大值是________.【答案】516.已知a、b是正实数,且满足ab=a+b+3,则a+b的取值范围是________.【答案】[6,+∞)【解析】 a、b是正实数且ab=a+b+3,故a、b可视为一元二次方程x2-mx+m+3=0的两个根,其中a+b=m,ab=m+3,要使方程有两个正根,应有解得m≥6,即a+b≥6,故a+b的取值范围是[6,+∞).17.已知x>0,比较x与ln(1+x)的大小,结果为________.【答案】x>ln(1+x)【解析】解法一:令x=1,则有1>ln2...