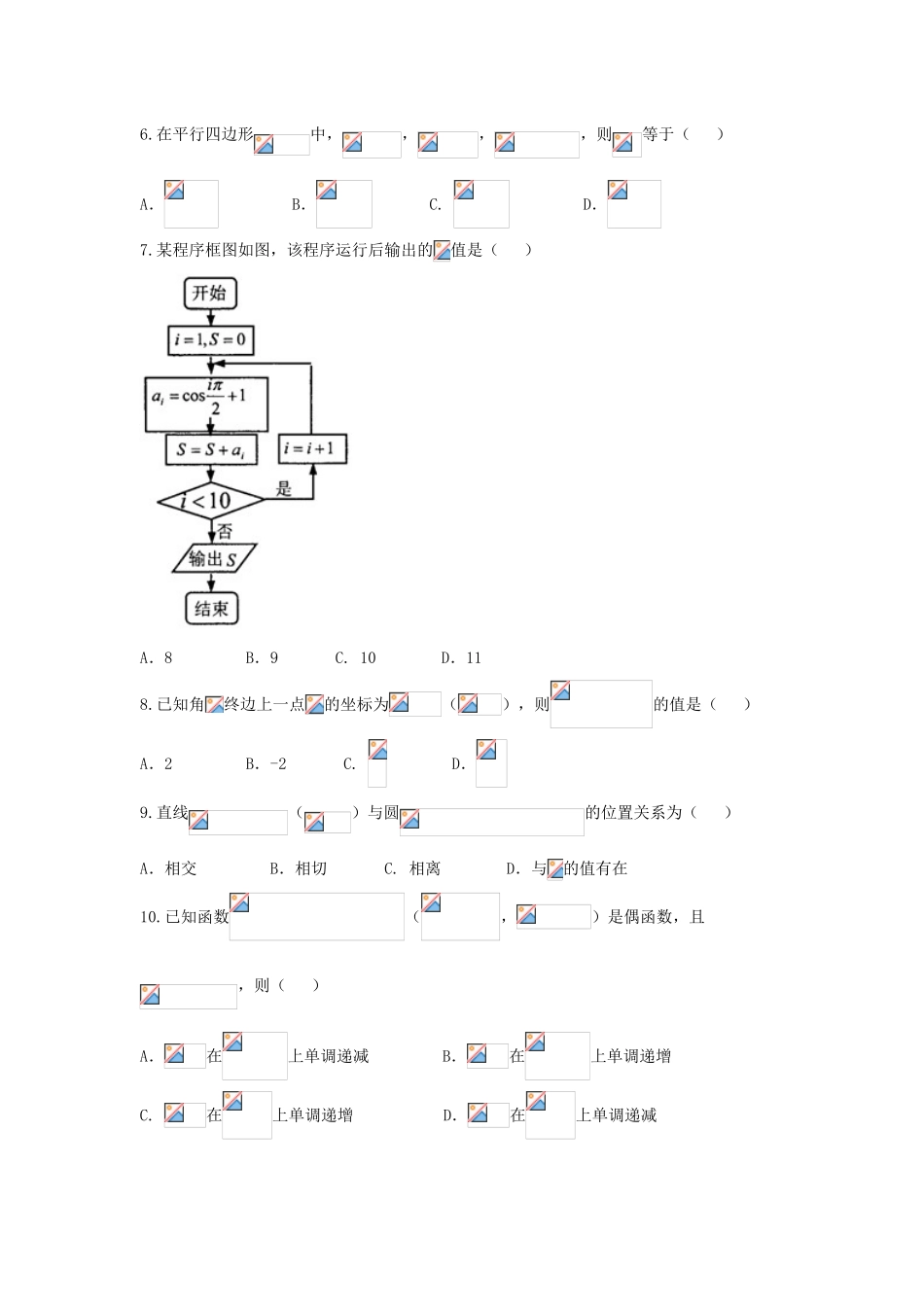
2016-2017学年度第二学期教学质量检查高一数学一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.的值为()A.B.C.D.2.某高级中学共有学生1500人,各年级学生人数如下表,现用分层抽样的方法在全校抽取45名学生,则在高一、高二、高三年级抽取的学生人数分别为()高一高二高三人数600500400A.12,18,15B.18,12,15C.18,15,12D.15,15,153.远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,就是现在人们熟悉的“进位制”,下图所示的是一位母亲记录的孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满六进一,根据图示可知,孩子已经出生的天数是()A.36B.56C.91D.3364.一个人投篮时连续投两次,则事件“至多投中一次”的互斥事件是()A.只有一次投中B.两次都不中C.两次都投中D.至少投中一次5.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒,绿灯持续时间为45秒,若一名行人来到该路口遇到红灯,则至少需要等街15秒才出现绿灯的概率为()A.B.C.D.6.在平行四边形中,,,,则等于()A.B.C.D.7.某程序框图如图,该程序运行后输出的值是()A.8B.9C.10D.118.已知角终边上一点的坐标为(),则的值是()A.2B.-2C.D.9.直线()与圆的位置关系为()A.相交B.相切C.相离D.与的值有在10.已知函数(,)是偶函数,且,则()A.在上单调递减B.在上单调递增C.在上单调递增D.在上单调递减11.已知在中,是的垂心,点满足:,则的面积与的面积之比是()A.B.C.D.12.若关于的不等式在上恒成立,则实数的最大值为()A.B.C.D.1二、填空题(每题5分,满分20分,将答案填在答题纸上)13.在空间直角坐标系中,已知,,则.14.下图是2016年在巴西举行的奥运会上,七位评委为某体操运动员的单项比赛打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为.15.已知扇形的周长为10,面积为4,则扇形的中心角等于(弧度).16.如图,等腰梯形的底边长分别为8和6,高为7,圆为等腰梯形的外接圆,对于平面内两点,(),若圆上存在点,使得,则正实数的取值范围是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知,是互相垂直的两个单位向量,,.(1)求和的夹角;(2)若,求的值.18.东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限(单位:年,)和所支出的维护费用(单位:万元)厂家提供的统计资料如下:(1)请根据以上数据,用最小二乘法原理求出维护费用关于的线性回归方程;(2)若规定当维护费用超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.参考公式:最小二乘估计线性回归方程中系数计算公式:,19.某学校进行体验,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50个身高介于155到195之间),现将抽取结果按如下方式分成八组:第一组,第二组,…,第八组,并按此分组绘制如图所示的频率分布直方图,其中第六组和第七组还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.(1)补全频率分布直方图;(2)根据频率分布直方图估计这50位男生身高的中位数;(3)用分层抽样的方法在身高为内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在内的概率.20.函数的部分图象如图所示,为图象的最高点,为图象的最低点,且为正三角形.(1)求的值域及的值;(2)若,且,求的值.21.已知圆,直线过定点,为坐标原点.(1)若圆截直线的弦长为,求直线的方程;(2)若直线的斜率为,直线与圆的两个交点为,且,求斜率的取值范围.22.已知,,(1)用表示;(2)若关于的方程为,试讨论该方程根的个数及相应实数的取值范围.2016—2017学年度第二学期教学质量检查高一数学参考答案一、选择题(每小题5分,共60分)题号123456789101112答案ACBCDCBDADAB二、填空题(每小题5分,满分20分)13.14.15.16.三、解答题:17.【解析】(1)因为,是互相垂直的单位向量,所以设与的夹角为,故...