高考数学一轮复习 第二章 函数概念与基本初等函数Ⅰ 2.3 函数的奇偶性与周期性真题演练集训 理 新人教A版-新人教A版高三全册数学试题VIP免费

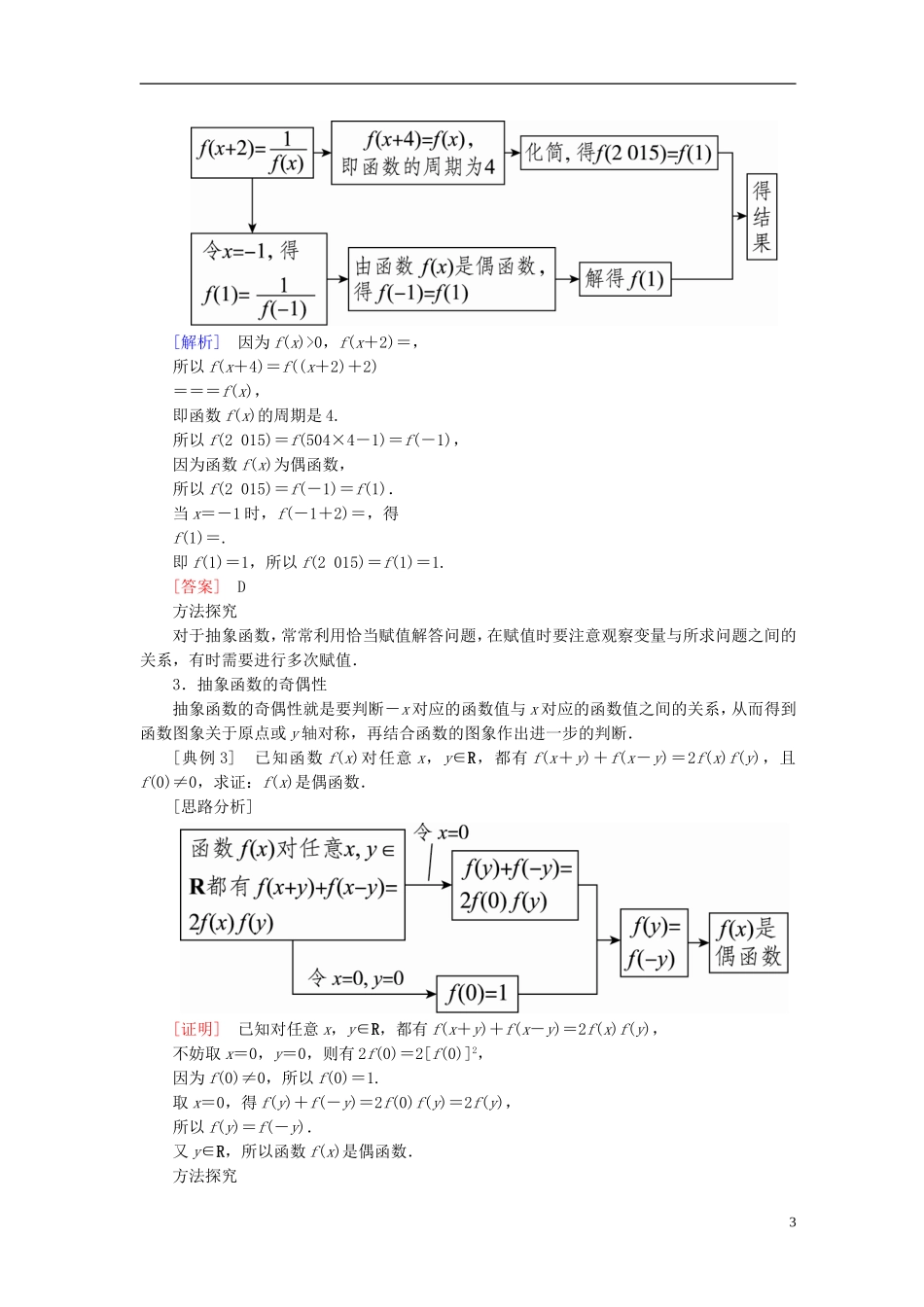
2018版高考数学一轮复习第二章函数概念与基本初等函数Ⅰ2.3函数的奇偶性与周期性真题演练集训理新人教A版1．[2015·福建卷]下列函数为奇函数的是()A．y＝B．y＝|sinx|C．y＝cosxD．y＝ex－e－x答案：D解析：对于D，f(x)＝ex－e－x的定义域为R，f(－x)＝e－x－ex＝－f(x)，故y＝ex－e－x为奇函数．而y＝的定义域为{x|x≥0}，不具有对称性，故y＝为非奇非偶函数．y＝|sinx|和y＝cosx为偶函数．2．[2014·新课标全国卷Ⅰ]设函数f(x)，g(x)的定义域都为R，且f(x)是奇函数，g(x)是偶函数，则下列结论中正确的是()A．f(x)g(x)是偶函数B．|f(x)|g(x)是奇函数C．f(x)|g(x)|是奇函数D．|f(x)g(x)|是奇函数答案：C解析：A：令h(x)＝f(x)g(x)，则h(－x)＝f(－x)·g(－x)＝－f(x)g(x)＝－h(x)，∴h(x)是奇函数，A错．B：令h(x)＝|f(x)|g(x)，则h(－x)＝|f(－x)|·g(－x)＝|－f(x)|g(x)＝|f(x)|g(x)＝h(x)，∴h(x)是偶函数，B错．C：令h(x)＝f(x)|g(x)|，则h(－x)＝f(－x)|g(－x)|＝－f(x)|g(x)|，∴h(x)是奇函数，C正确．D：令h(x)＝|f(x)g(x)|，则h(－x)＝|f(－x)g(－x)|＝|－f(x)g(x)|＝|f(x)g(x)|＝h(x)，∴h(x)是偶函数，D错．3．[2016·山东卷]已知函数f(x)的定义域为R.当x＜0时，f(x)＝x3－1；当－1≤x≤1时，f(－x)＝－f(x)；当x＞时，f＝f，则f(6)＝()A．－2B．－1C．0D．2答案：D解析：由题意可知，当－1≤x≤1时，f(x)为奇函数，且当x>时，f(x＋1)＝f(x)，所以f(6)＝f(5×1＋1)＝f(1)．而f(1)＝－f(－1)＝－[(－1)3－1]＝2，所以f(6)＝2.故选D.4．[2015·新课标全国卷Ⅰ]若函数f(x)＝xln(x＋)为偶函数，则a＝________.答案：1解析： f(x)为偶函数，∴f(－x)－f(x)＝0恒成立，∴－xln(－x＋)－xln(x＋)＝0恒成立，∴xlna＝0恒成立，∴lna＝0，即a＝1.5．[2016·四川卷]已知函数f(x)是定义在R上的周期为2的奇函数，当00，f(x＋2)＝，对任意x∈R恒成立，则f(2015)＝()A．4B．3C．2D．1[思路分析]2[解析]因为f(x)>0，f(x＋2)＝，所以f(x＋4)＝f((x＋2)＋2)＝＝＝f(x)，即函数f(x)的周期是4.所以f(2015)＝f(504×4－1)＝f(－1)，因为函数f(x)为偶函数，所以f(2015)＝f(－1)＝f(1)．当x＝－1时，f(－1＋2)＝，得f(1)＝.即f(1)＝1，所以f(2015)＝f(1)＝1.[答案]D方法探究对于抽象函数，常常利用恰当赋值解答问题，在赋值时要注意观察变量与所求问题之间的关系，有时需要进行多次赋值．3．抽象函数的奇偶性抽象函数的奇偶性就是要判断－x对应的函数值与x对应的函数值之间的关系，从而得到函数图象关于原点或y轴对称，再结合函数的图象作出进一步的判断．[典例3]已知函数f(x)对任意x，y∈R，都有f(x...