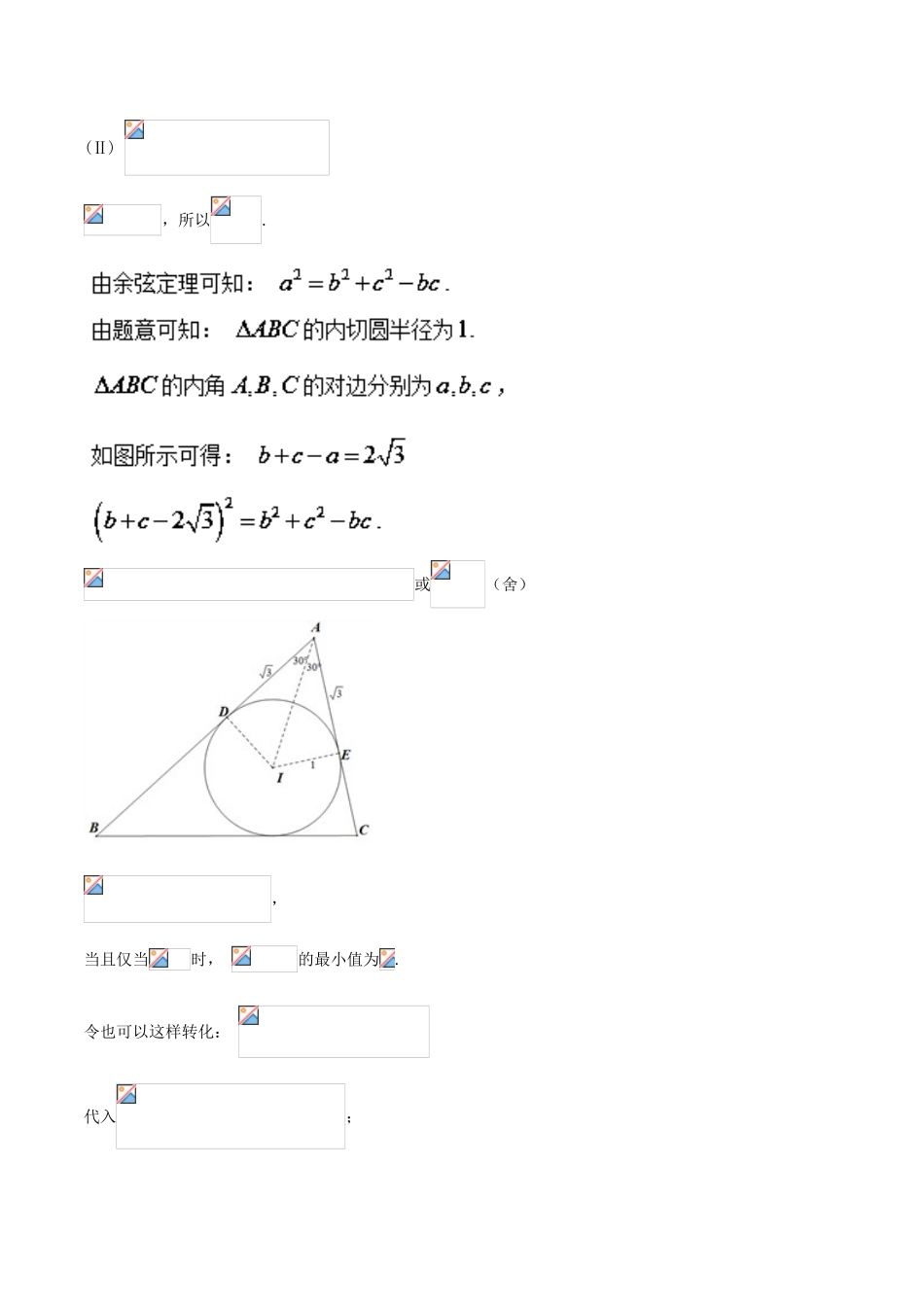
专题04大题好拿分(提升版)理1.设函数(Ⅰ)求的单调增区间;(Ⅱ)已知的内角分别为,若,且能够盖住的最大圆面积为,求的最小值.【答案】(Ⅰ);(Ⅱ)6.试题解析:(Ⅰ)..的单调增区间为.(Ⅱ),所以.或(舍),当且仅当时,的最小值为.令也可以这样转化:代入;或(舍);,当且仅当时,的最小值为.2.设向量,函数.(1)求在上的值域;(2)已知,先将的图象向右平移个单位长度,再把得到的图象上所有点的横坐标缩短到原来的,纵坐标不变,然后再把得到的图象向上平移个单位长度,得到的图象,已知的部分图象如图所示,求的值.【答案】(1);(2)2.试题解析:(1)因为,因为,所以,所以,所以.所以.【点睛】本题考查两个向量的数量积公式,三角函数的恒等变换及化简求值,函数的图象变换规律等问题.其中(2)解题的关键是根据图像得到3.已知数列满足,.(1)是否能找到一个定义在的函数(是常数)使得数列是公比为3的等比数列,若存在,求出的通项公式;若不存在,说明理由;(2)记,若不等式对任意都成立,求实数的取值范围.【答案】(1);(2).【解析】试题分析:(1)由可得,结合,对应项系数相等列不等式组求解即可;(2)先利用分组求和法求得,化简可得,∴,∴.(2)∴,由,得.设,则,当时,∴时,.容易验证,当时,,∴,∴的取值范围为.4.已知数列是公差为正数的等差数列,其前项和为,且,.(1)求数列的通项公式;(2)数列满足,.①求数列的通项公式;②是否存在正整数,(),使得,,成等差数列?若存在,求出,的值;若不存在,请说明理由.【答案】(1);(2)①;②存在正整数,,使得,,成等差数列.试题解析:(1)设数列的公差为,则.由,,得解得或(舍去).所以.(2)①因为,,所以,,即,,…,,()累加得,所以,也符合上式,故,.②假设存在正整数、(),使得,,成等差数列,则.又,,,所以,即,化简得:,当,即时,(舍去);当,即时,符合题意.所以存在正整数,,使得,,成等差数列.5.为了增强高考与高中学习的关联度,考生总成绩由统一高考的语文、数学、外语3个科目成绩和高中学业水平考试3个科目成绩组成.保持统一高考的语文、数学、外语科目不变,分值不变,不分文理科,外语科目提供两次考试机会.计入总成绩的高中学业水平考试科目,由考生根据报考高校要求和自身特长,在思想政治、历史、地理、物理、化学、生物、信息技术七科目中自主选择三科.(1)某高校某专业要求选考科目物理,考生若要报考该校该专业,则有多少种选考科目的选择;(2)甲、乙、丙三名同学都选择了物理、化学、历史组合,各学科成绩达到二级的概率都是0.8,且三人约定如果达到二级不参加第二次考试,达不到二级参加第二次考试,如果设甲、乙、丙参加第二次考试的总次数为,求的分布列和数学期望.【答案】(1)15(2)见解析(2)因为甲乙丙三名同学每一学科达到二级的概率都相同且相互独立,所以参加第二次考试的总次数服从二项分布,所以分布列为所以的数序期望.6.某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间,需求量为300瓶;如果最高气温低于20,需求量为200瓶,为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量(单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为(单位:元).当六月份这种酸奶一天的进货量(单位:瓶)为多少时,的数学期望达到最大值?【答案】(1)分布列为:(2).【解析】试题分析:(1)由题意知的可能取值为200,300,500,分别求出相应的概率,由此能求出的分布列.(2)当时,,;当时,;当时,;当时,.从而得到当时,最大值为520元.试题解析:(1)易知需求量可取200,300,500,,,,则分布列为:综上所述,当时,取到最...