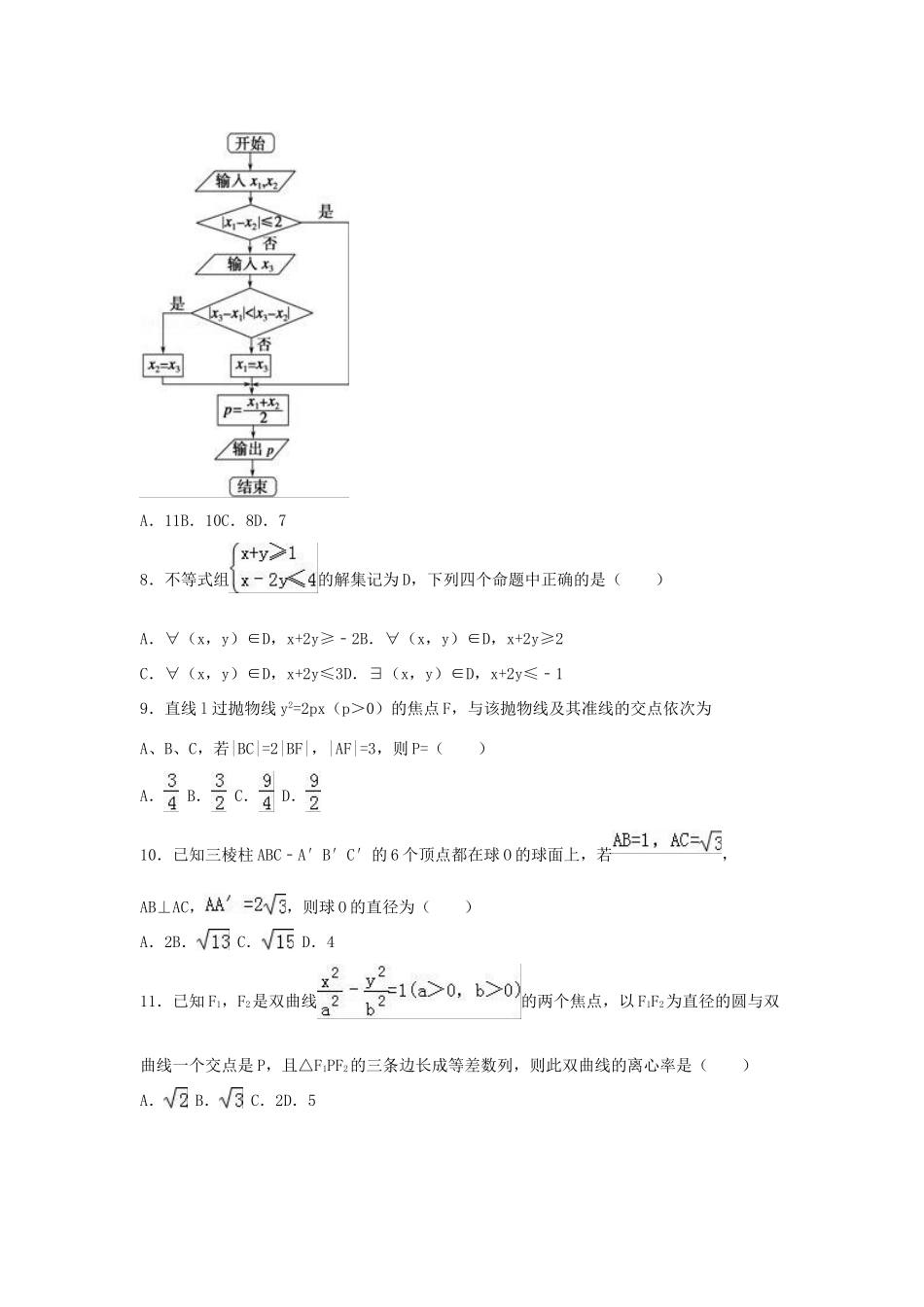
2016年广西桂林市、崇左市高考数学模拟试卷(文科)(4月份)一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知两集合,则A∩B=()A.[﹣2,0)B.C.D.[1,+∞)2.复数z=(a+i)(1﹣i),a∈R,i是虚数单位.若|z|=2,则a=()A.1B.﹣1C.0D.±13.若向量,满足:||=1,(+)⊥,(3+)⊥,则||=()A.3B.C.1D.4.若函数f(x)=lnx﹣ax在区间(1,+∞)上单调递减,则a的取值范围是()A.[1,+∞)B.[﹣1,+∞)C.(﹣∞,1]D.(﹣∞,﹣1]5.将函数f(x)=sinωx(ω>0)的图象向右平移个单位长度,所得图象关于点对称,则ω的最小值是()A.B.1C.D.26.一个几何体三视图如图所示,则该几何体的表面积等于()A.2πB.4πC.6+(2+)πD.(4+2)π7.如图中,x1,x2,x3为某次考试三个评阅人对同一道题的独立评分,P为该题的最终得分.当x1=6,x2=9,p=8.5时,x3等于()A.11B.10C.8D.78.不等式组的解集记为D,下列四个命题中正确的是()A.∀(x,y)∈D,x+2y≥﹣2B.∀(x,y)∈D,x+2y≥2C.∀(x,y)∈D,x+2y≤3D.∃(x,y)∈D,x+2y≤﹣19.直线l过抛物线y2=2px(p>0)的焦点F,与该抛物线及其准线的交点依次为A、B、C,若|BC|=2|BF|,|AF|=3,则P=()A.B.C.D.10.已知三棱柱ABC﹣A′B′C′的6个顶点都在球O的球面上,若,AB⊥AC,,则球O的直径为()A.2B.C.D.411.已知F1,F2是双曲线的两个焦点,以F1F2为直径的圆与双曲线一个交点是P,且△F1PF2的三条边长成等差数列,则此双曲线的离心率是()A.B.C.2D.512.设f(x)是定义在R上的偶函数,对于任意的x∈R,都有f(x﹣2)=f(2+x),且当x∈[﹣2,0]时,f(x)=﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0恰有3个不同的实数解,则a的取值范围是()A.(1,2)B.(2,+∞)C.(1,)D.(,2)二.填空题:本大题共4小题,每小题5分.13.设Sn是等差数列{an}的前n项和,若a1=2,S5=12,则a6等于.14.若点(n,3)在函数y=3x的图象上,则的值是.15.已知圆C:x2﹣2x+y2+4y+1=0,经过点P(3,4)的直线分别与圆C相切于点A、B,则三角形ABC的面积等于.16.已知正方形ABCD的边长为2,点P、Q分别是边AB、BC边上的动点,且,则的最小值为.三.解答题:解答应写出文字说明,证明过程或演算步骤.17.如图,在四边形ABCD中,AB=3,AD=BC=CD=2,A=60°.(Ⅰ)求sin∠ABD的值;(Ⅱ)求△BCD的面积.18.有7位歌手(1至7号)参加一场歌唱比赛,由550名大众评委现场投票决定歌手名次,根据年龄将大众评委分为5组,各组的人数如下:组别ABCDE人数5010020015050(Ⅰ)为了调查大众评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从B组中抽取了6人.请将其余各组抽取的人数填入表.组别ABCDE人数5010020015050抽取人数6(Ⅱ)在(Ⅰ)中,若A,C两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.19.如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=4,.(Ⅰ)设M是PC上的一点,证明:平面MBD⊥平面PAD;(Ⅱ)求四棱锥P﹣ABCD的体积.20.设a>0且a≠0,函数.(1)当a=2时,求曲线y=f(x)在(3,f(3))处切线的斜率;(2)求函数f(x)的极值点.21.已知圆C:(x+1)2+y2=20,点B(l,0).点A是圆C上的动点,线段AB的垂直平分线与线段AC交于点P.(I)求动点P的轨迹C1的方程;(Ⅱ)设,N为抛物线C2:y=x2上的一动点,过点N作抛物线C2的切线交曲线Cl于P,Q两点,求△MPQ面积的最大值.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.[选修4-1:几何证明选讲]22.如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.(1)求证:O、B、D、E四点共圆;(2)求证:2DE2=DM•AC+DM•AB.[选修4-4:坐标系与参数方程]23.将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得...