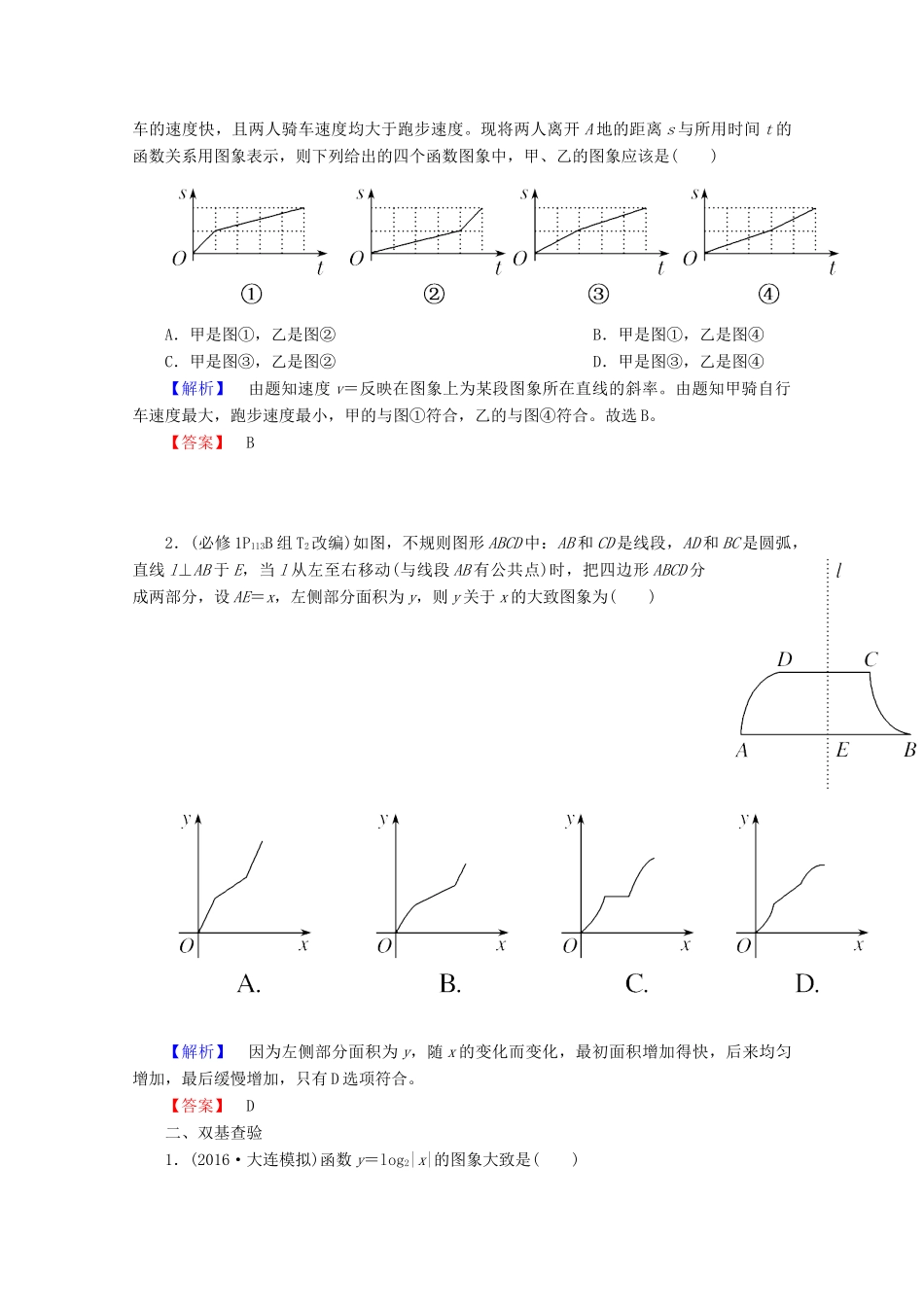
第七节函数的图象☆☆☆2017考纲考题考情☆☆☆考纲要求真题举例命题角度1.在实际情境中,会根据不同的需要选择图象法、列表法、解析法表示函数;2.会运用函数图象理解和研究函数的性质,解决方程解的个数与不等式解的问题。2016,全国卷Ⅰ,7,5分(函数图象的识别)2016,全国卷Ⅱ,12,5分(函数图象的应用)2016,山东卷,15,5分(函数图象的应用)2015,全国卷Ⅰ,12,5分(函数图象、单调性的综合应用)1.由实际问题中的函数变化过程选图、根据解析式选图、解决函数的性质问题是高考的热点;2.常与函数的性质(单调性、奇偶性、周期性、对称性、零点)、方程、不等式等知识交汇考查。微知识小题练自|主|排|查1.利用描点法作函数图象基本步骤是列表、描点、连线。首先:(1)确定函数的定义域;(2)化简函数解析式;(3)讨论函数的性质(奇偶性、单调性、周期性、对称性等)。其次:列表(尤其注意特殊点、零点、最大值点、最小值点、与坐标轴的交点等),描点,连线。2.利用图象变换法作函数的图象(1)平移变换:y=f(x)――――――――――→y=f(x-a);y=f(x)――――――――――→y=f(x)+b。(2)伸缩变换:y=f(x)y=f(ωx);y=f(x)――――――――――――――――――――――→y=Af(x)。(3)对称变换:y=f(x)―――――→y=-f(x);y=f(x)――――――→y=f(-x);y=f(x)――――――→y=-f(-x)。(4)翻折变换:y=f(x)――――――――――――――――→y=f(|x|);y=f(x)――――――――――――――――→y=|f(x)|。微点提醒1.在解决函数图象的变换问题时,要遵循“只能对函数关系式中的x,y变换”的原则。2.注意含绝对值符号的函数图象的对称性,如y=f(|x|)与y=|f(x)|的图象一般是不同的。3.记住几个重要结论(1)函数y=f(x)与y=f(2a-x)的图象关于直线x=a对称。(2)函数y=f(x)与y=2b-f(2a-x)的图象关于点(a,b)中心对称。(3)若函数y=f(x)对定义域内任意自变量x满足:f(a+x)=f(a-x),则函数y=f(x)的图象关于直线x=a对称。小|题|快|练一、走进教材1.(必修1P112A组T4改编)甲、乙二人同时从A地赶往B地,甲先骑自行车到两地的中点再改为跑步,乙先跑步到中点再改为骑自行车,最后两人同时到达B地。已知甲骑车比乙骑车的速度快,且两人骑车速度均大于跑步速度。现将两人离开A地的距离s与所用时间t的函数关系用图象表示,则下列给出的四个函数图象中,甲、乙的图象应该是()A.甲是图①,乙是图②B.甲是图①,乙是图④C.甲是图③,乙是图②D.甲是图③,乙是图④【解析】由题知速度v=反映在图象上为某段图象所在直线的斜率。由题知甲骑自行车速度最大,跑步速度最小,甲的与图①符合,乙的与图④符合。故选B。【答案】B2.(必修1P113B组T2改编)如图,不规则图形ABCD中:AB和CD是线段,AD和BC是圆弧,直线l⊥AB于E,当l从左至右移动(与线段AB有公共点)时,把四边形ABCD分成两部分,设AE=x,左侧部分面积为y,则y关于x的大致图象为()【解析】因为左侧部分面积为y,随x的变化而变化,最初面积增加得快,后来均匀增加,最后缓慢增加,只有D选项符合。【答案】D二、双基查验1.(2016·大连模拟)函数y=log2|x|的图象大致是()【解析】函数y=log2|x|为偶函数,作出x>0时y=log2x的图象,再根据图象关于y轴对称,作出y轴左侧的图象,应选C。【答案】C2.函数f(x)=ln(x2+1)的图象大致是()A.B.C.D.【解析】由函数解析式可知f(x)=f(-x),即函数为偶函数,排除C;由函数图象过(0,0)点,排除B,D。故选A。【答案】A3.已知函数y=f(x+1)的图象过点(3,2),则函数y=f(x)的图象关于x轴对称的图象过定点()A.(1,-2)B.(2,-2)C.(3,-2)D.(4,-2)【解析】由已知有f(4)=2,故函数y=f(x)的图象一定过点(4,2),函数y=f(x)的图象关于x轴对称的图象过定点(4,-2)。故选D。【答案】D4.函数f(x)的图象向右平移1个单位长度,所得图象与曲线y=ex关于y轴对称,则f(x)=()A.ex+1B.ex-1C.e-x+1D.e-x-1【解析】依题意,与曲线y=ex关于y轴对称的曲线是y=e-x,于是f(x)相当于y=e-x的图象向左平移1个单位得到的,∴f(x)=e-(x+1)=e-x-1。故选D。...