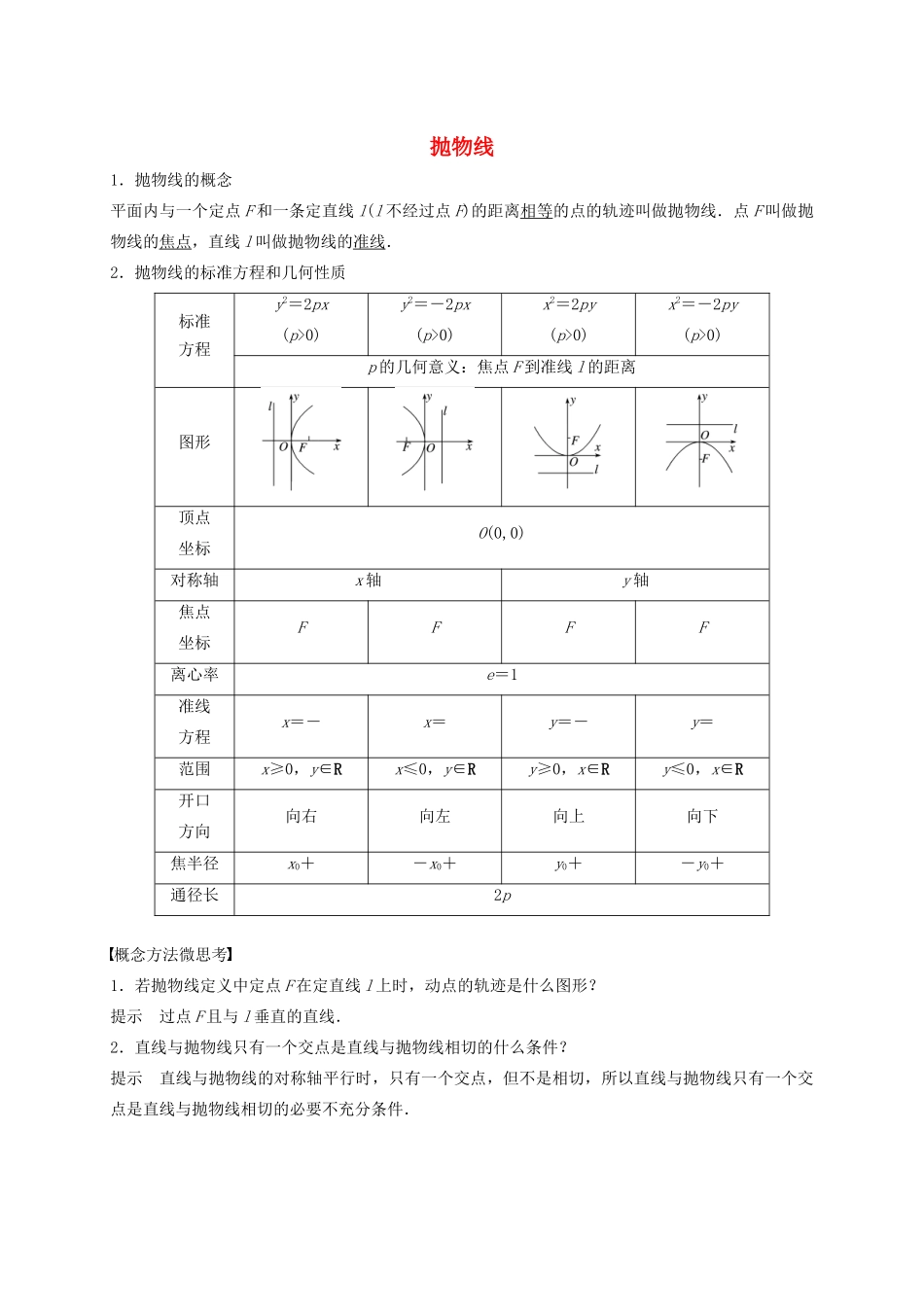
抛物线1.抛物线的概念平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.2.抛物线的标准方程和几何性质标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)p的几何意义:焦点F到准线l的距离图形顶点坐标O(0,0)对称轴x轴y轴焦点坐标FFFF离心率e=1准线方程x=-x=y=-y=范围x≥0,y∈Rx≤0,y∈Ry≥0,x∈Ry≤0,x∈R开口方向向右向左向上向下焦半径x0+-x0+y0+-y0+通径长2p概念方法微思考1.若抛物线定义中定点F在定直线l上时,动点的轨迹是什么图形?提示过点F且与l垂直的直线.2.直线与抛物线只有一个交点是直线与抛物线相切的什么条件?提示直线与抛物线的对称轴平行时,只有一个交点,但不是相切,所以直线与抛物线只有一个交点是直线与抛物线相切的必要不充分条件.1.(2020•新课标Ⅰ)已知为抛物线上一点,点到的焦点的距离为12,到轴的距离为9,则A.2B.3C.6D.9【答案】C【解析】为抛物线上一点,点到的焦点的距离为12,到轴的距离为9,因为抛物线上的点到焦点的距离和到准线的距离相等,故有:;故选.2.(2020•北京)设抛物线的顶点为,焦点为,准线为.是抛物线上异于的一点,过作于,则线段的垂直平分线A.经过点B.经过点C.平行于直线D.垂直于直线【答案】B【解析】不妨设抛物线的方程为,则,准线为为,不妨设,,设准线为与轴交点为,则,可得四边形为正方形,根据正方形的对角线互相垂直,故可得线段的垂直平分线,经过点,故选.3.(2020•浙江)已知点,,.设点满足,且为函数图象上的点,则A.B.C.D.【答案】D【解析】点,,.设点满足,可知的轨迹是双曲线的右支上的点,为函数图象上的点,即在第一象限的点,联立两个方程,解得,,所以.故选.4.(2019•天津)已知抛物线的焦点为,准线为.若与双曲线的两条渐近线分别交于点和点,且为原点),则双曲线的离心率为A.B.C.2D.【答案】D【解析】抛物线的焦点为,准线为.,准线的方程为,与双曲线的两条渐近线分别交于点和点,且为原点),,,,,,双曲线的离心率为.故选.5.(2019•新课标Ⅱ)若抛物线的焦点是椭圆的一个焦点,则A.2B.3C.4D.8【答案】D【解析】由题意可得:,解得.故选.6.(2018•全国)过抛物线的焦点且与轴垂直的直线与抛物线交于、两点,为坐标原点,则A.B.C.D.【答案】D【解析】的焦点坐标是,,则过焦点且垂直轴的直线是,代入得,故,.故选.7.(2018•新课标Ⅰ)设抛物线的焦点为,过点且斜率为的直线与交于,两点,则A.5B.6C.7D.8【答案】D【解析】抛物线的焦点为,过点且斜率为的直线为:,联立直线与抛物线,消去可得:,解得,,不妨,,,.则,,.故选.8.(2017•新课标Ⅰ)已知为抛物线的焦点,过作两条互相垂直的直线,,直线与交于、两点,直线与交于、两点,则的最小值为A.16B.14C.12D.10【答案】A【解析】方法一:如图,,直线与交于、两点,直线与交于、两点,由图象知要使最小,则与,与关于轴对称,即直线的斜率为1,又直线过点,则直线的方程为,联立方程组,则,,,,的最小值为,方法二:设直线的倾斜角为,则的倾斜角为,根据焦点弦长公式可得,,当时,的最小,最小为16,故选.9.(2020•海南)斜率为的直线过抛物线的焦点,且与交于,两点,则__________.【答案】【解析】由题意可得抛物线焦点,直线的方程为,代入并化简得,设,,,,则;,由抛物线的定义可得.故答案为:.10.(2019•上海)过曲线的焦点并垂直于轴的直线分别与曲线交于,,在上方,为抛物线上一点,,则__________.【答案】3【解析】过的焦点并垂直于轴的直线分别与交于,,在上方,依题意:得到:,,,设点,所以:为抛物线上一点,,则:,,,,,代入,得到:.故答案为:311.(2019•北京)设抛物线的焦点为,准线为,则以为圆心,且与相切的圆的方程为__________.【答案】【解析】如图,抛物线的焦点为,所求圆的圆心,且与准线相切,圆的半径为2.则所求圆的方程为.故答案为:.12.(2018•北京)已知直线过点且垂直于轴....