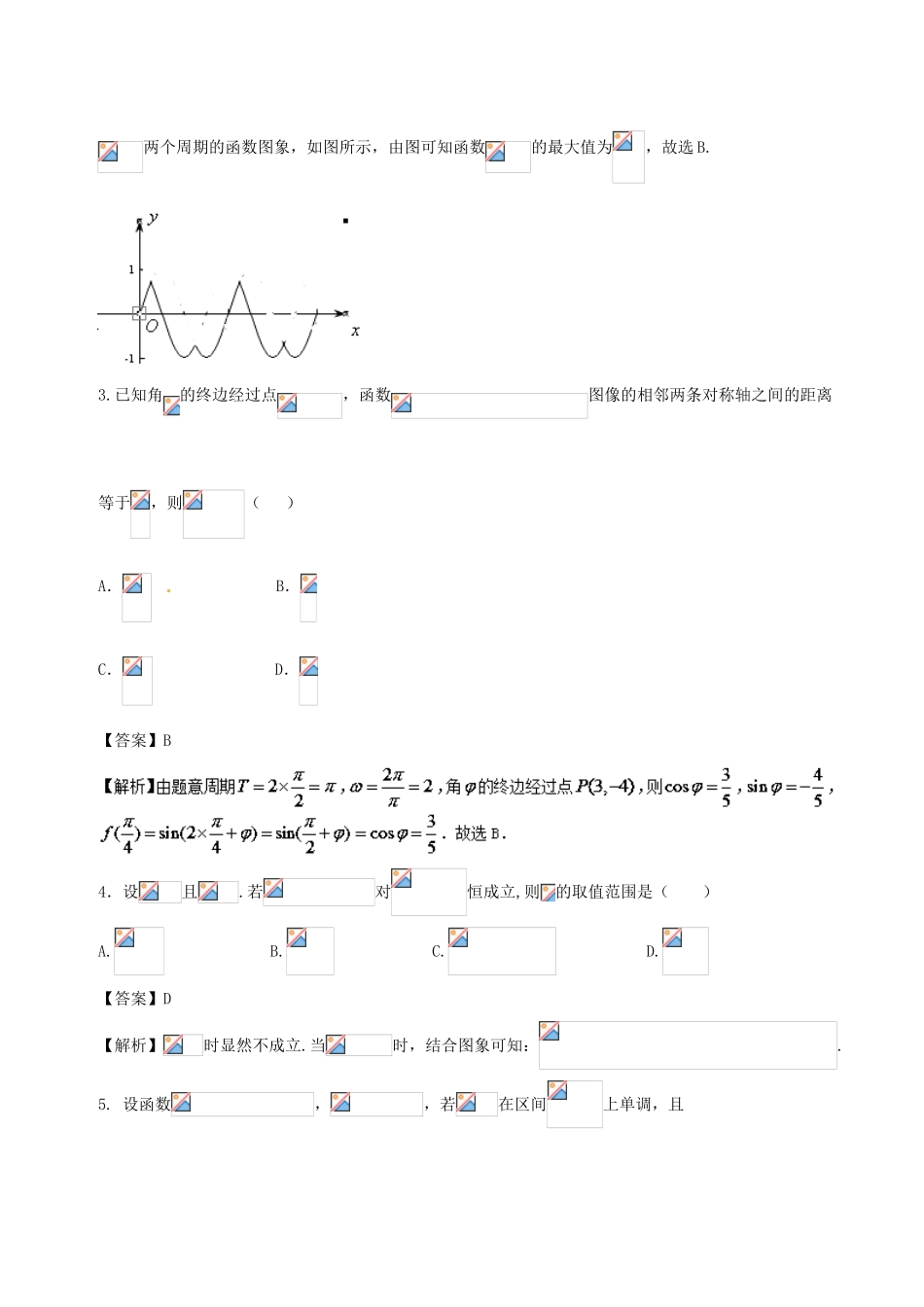
专题四三角函数的图象与性质测试卷(B卷)(测试时间:120分钟满分:150分)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.【2018届山东、湖北部分重点中学高三第一次联考】函数的单调递减区间为A.B.C.D.【答案】A2.定义一种运算令(),则函数的最大值是()A.1B.C.0D.【答案】B【解析】因为,所以,,画出函数两个周期的函数图象,如图所示,由图可知函数的最大值为,故选B.3.已知角的终边经过点,函数图像的相邻两条对称轴之间的距离等于,则()A.B.C.D.【答案】B4.设且.若对恒成立,则的取值范围是()A.B.C.D.【答案】D【解析】时显然不成立.当时,结合图象可知:.5.设函数,,若在区间上单调,且,则的最小正周期为()A.B.2πC.4πD.π【答案】D【解析】在区间上单调,,,即,又,为的一条对称轴,且,则为的一个对称中心,由于,所以与为同一周期里相邻的对称轴和对称中心,则.选D.6.函数的图象关于点成中心对称,则最小的的值为()A.B.C.D.【答案】C【解析】由题意得,当时,,即,时最小,此时,故选C.7.如果,那么函数的值域是()A.B.C.D.【答案】D8.当时,函数取得最小值,则函数的一个单调递增区间是()A.B.C.D.【答案】C【解析】当时,函数取得最小值,即,解得,所以,从而.9.已知函数,若是的一个单调递增区间,则的取值范围是()A.B.C.D.【答案】C【解析】由于是的一个单调递增区间,即是的一个单调递减区间,令可得,且,又因为,解得故选C.10.已知直线是函数图象的一条对称轴,则取得最小值时的集合为()A.B.C.D.【答案】C11.已知函数,其中,若的值域是,则的取值范围是()A.B.C.D.【答案】B【解析】因为的值域为,所以由函数的图象可知,所以解得,所以的取值范围是,故选B.12.已知函数,其图象相邻两条对称轴之间的距离为,且函数是偶函数,下列判断正确的是()A.函数的最小正周期为B.函数的图象关于点对称C.函数的图象关于直线对称D.函数在上单调递增【答案】D第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.【2018届湖北省宜昌市葛洲坝中学高三9月月考】函数的最小正周期为_____________.【答案】【解析】由正切函数的周期公式得:故答案为.14.给出下列命题:(1)函数不是周期函数;(2)函数在定义域内为增函数;(3)函数的最小正周期为;(4)函数,的一个对称中心为.其中正确命题的序号是.【答案】(1)(4)15.给出下列命题:①存在实数,使;②存在实数,使;③函数是偶函数;④是函数的一条对称轴方程;⑤若是第一象限角,且,则.以上命题是真命题的是。【答案】③④【解析】①;②;③是偶函数;④当时,,所以是函数的一条对称轴方程;⑤取,满足“是第一象限角,且”,但.故选③④.16.对于函数给出下列四个命题:①该函数是以为最小正周期的周期函数;②当且仅当时,该函数取得最小值-1;③该函数的图象关于对称;④当且仅当时,.其中正确命题的序号是___________.(请将所有正确命题的序号都填上)【答案】③④【解析】可作出函数在的图象如图所示,由图象可知函数的最小正周期为,在或时,该函数有最小值,故①②错误,由图象可知函数图象关于直线对称,在时,,故(3)(4)正确.因此,本题的正确答案为③④.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.【2018届新疆呼图壁县第一中学高三9月月考】已知函数。(Ⅰ)求f(x)的最小正周期:(Ⅱ)求f(x)在区间上的最大值和最小值。【答案】(1)T=2π;(2)f(x)的最大值为,最小值为-1.18.已知函数的最大值为,其图像的相邻两条对称轴之间的距离为.(1)求函数对称中心的坐标;(2)求函数在区间上的值域.【答案】(1);(2).【解析】因为,所以,所以又因为图像的相邻两条对称轴之间的距离为,所以所以,故所以(1)令所以故对称中心为(2)所以函数在的值域为:.19.已知函数.(1)请用“五点法”画出函数在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);(2)当时,求函...