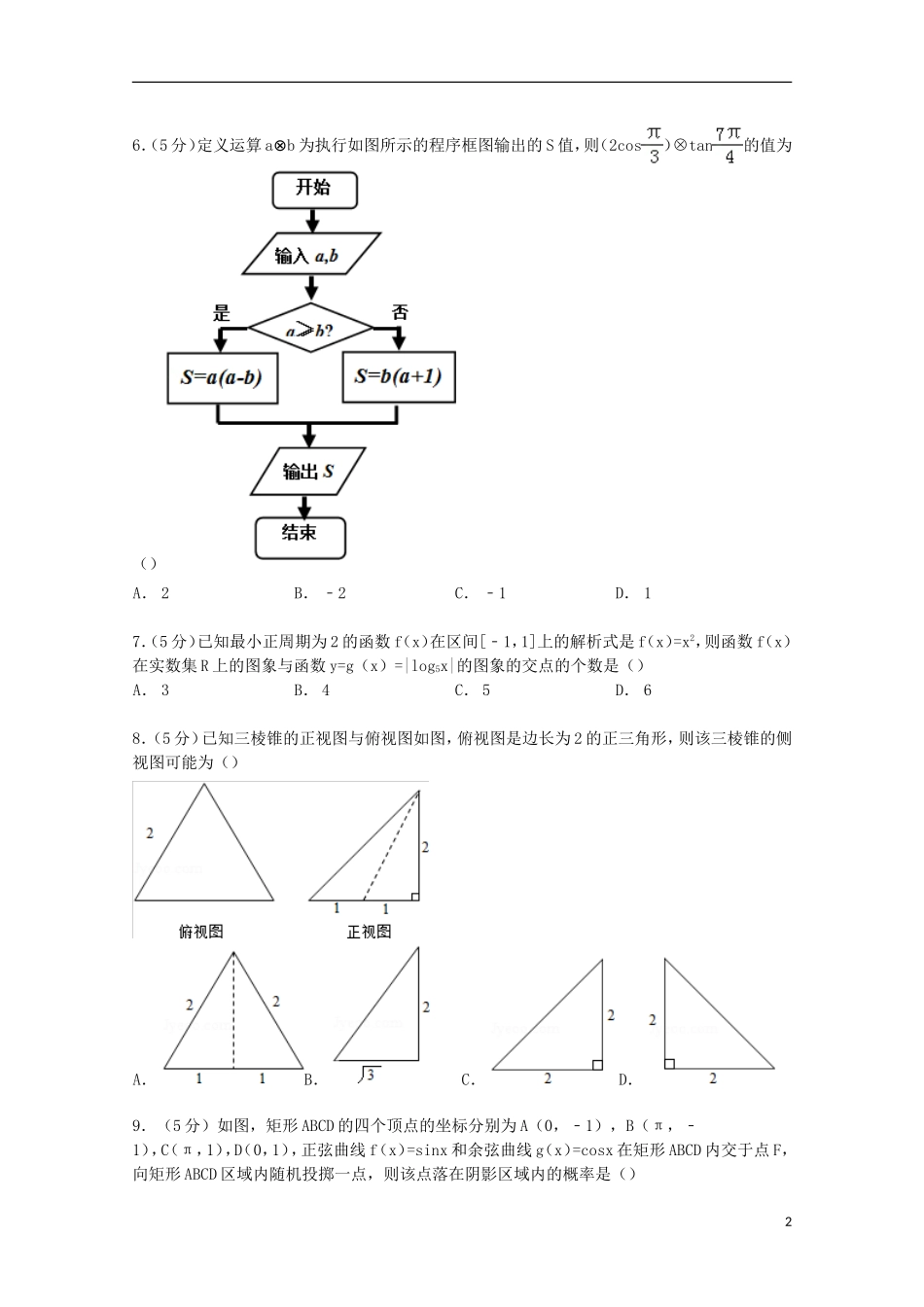
湖南省长望浏宁四县2015届高考数学模拟试卷(理科)(3月份)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.(5分)集合A={x∈N|x≤6},B={x∈R|x2﹣3x>0},则A∩B=()A.{x|3≤x<6}B.{3,4,5}C.{x|3<x≤6}D.{4,5,6}2.(5分)设a∈R,则“<1”是“a>1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(5分)已知函数y=f(x)﹣x是偶函数,且f(2)=1,则f(﹣2)=()A.﹣3B.﹣1C.1D.24.(5分)(x2+2)(﹣1)5的展开式的常数项是()A.2B.3C.﹣2D.﹣35.(5分)如图,在△OAB中,P为线段AB上的一点,=x+y,且=3,则()A.x=,y=B.x=,y=C.x=,y=D.x=,y=16.(5分)定义运算a⊗b为执行如图所示的程序框图输出的S值,则(2cos)⊗tan的值为()A.2B.﹣2C.﹣1D.17.(5分)已知最小正周期为2的函数f(x)在区间[﹣1,1]上的解析式是f(x)=x2,则函数f(x)在实数集R上的图象与函数y=g(x)=|log5x|的图象的交点的个数是()A.3B.4C.5D.68.(5分)已知三棱锥的正视图与俯视图如图,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为()A.B.C.D.9.(5分)如图,矩形ABCD的四个顶点的坐标分别为A(0,﹣1),B(π,﹣1),C(π,1),D(0,1),正弦曲线f(x)=sinx和余弦曲线g(x)=cosx在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是()2A.B.C.D.10.(5分)若数列{an}满足:存在正整数T,对于任意正整数n都有an+T=an成立,则称数列{an}为周期数列,周期为T.已知数列{an}满足a1=m(m>0),则下列结论中错误的是()A.若a3=4,则m可以取3个不同的值B.若,则数列{an}是周期为3的数列C.∀T∈N*且T≥2,存在m>1,使得{an}是周期为T的数列D.∃m∈Q且m≥2,使得数列{an}是周期数列二、填空题:本大题共3小题,考生作答5小题,每小题5分,共25分.(一)选做题(请考生在第11、12、13三题中任选两题作答,若全做,则按前两题记分)11.(5分)(坐标系与参数方程选做题)在直角坐标系xOy中,直线l的参数方程为(t为参数),以原点O为极点,以x轴的正半轴为极轴建立极坐标,曲线C的极坐标方程为,则直线l和曲线C的公共点有个.12.(5分)如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为.13.若2x+3y+4z=11,则x2+y2+z2的最小值为.(二)必做题(14-16题)314.(5分)设实数x,y满足,向量=(2x﹣y,m),=(﹣1,1),若∥,则实数m的最小值为.15.(5分)已知两定点A(﹣1,0)和B(1,0),动点P(x,y)在直线l:y=x+2上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为.16.(5分)定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)=,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是.三、解答题:本大题共6个小题,满分75分.解答应写出必要的文字说明,证明过程或演算步骤.17.(12分)“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动,若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.(1)若某被邀请者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?(2)假定(1)中被邀请到的3个人中恰有两个接受挑战,根据活动规定,现记X为接下来被邀请到的6个人中接受挑战的人数,求X的分布列和均值(数学期望).18.(12分)如图,摩天轮上一点P在t时刻距离地面高度满足y=Asin(ωt+φ)+b,φ∈[﹣π,π],已知某摩天轮的半径为50...