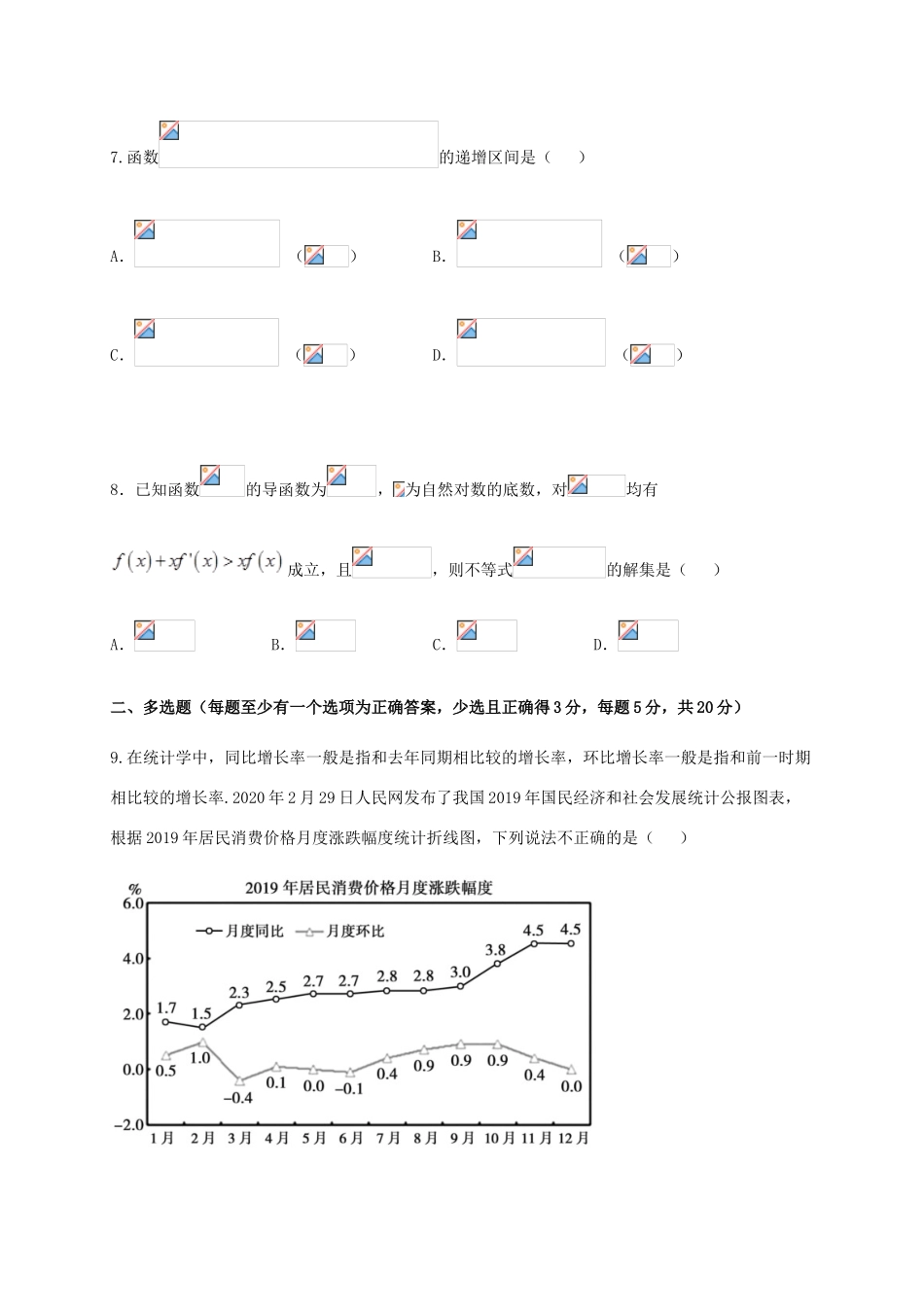
福建省福清西山学校高中部2021届高三数学9月月考试题一、单选题(每题只有一个选项是正确答案,每题5分,共40分)1.已知集合A={x|x2﹣5x+4<0,x∈Z},B={m,2},若A⊆B,则m=()A.5B.3C.2D.12.设复数且,则的虚部为()A.B.C.D.3..已知,,,则()A.B.C.D.4.如图,D是△ABC的边AB的中点,则向量等于()A.B.C.D.5.设为等差数列的前项和,若,则()A.B.C.D.6.已知,则()A.B.C.D.7.函数的递增区间是()A.()B.()C.()D.()8.已知函数的导函数为,为自然对数的底数,对均有成立,且,则不等式的解集是()A.B.C.D.二、多选题(每题至少有一个选项为正确答案,少选且正确得3分,每题5分,共20分)9.在统计学中,同比增长率一般是指和去年同期相比较的增长率,环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表,根据2019年居民消费价格月度涨跌幅度统计折线图,下列说法不正确的是()A.2019年我国居民每月消费价格与2018年同期相比有涨有跌B.2019年我国居民每月消费价格中2月消费价格最高C2019年我国居民每月消费价格逐月递增D.2019年我国居民每月消费价格3月份较2月份有所下降10.由函数的图象得到函数的图象的过程中,下列表述正确的是()A.先将的图象上各点的横坐标缩短到原来的(纵坐标不变),再向左平移个单位长度B.先将的图象上各点的横坐标缩短到原来的(纵坐标不变),再向左平移个单位长度C.先将的图象向左平移个单位长度,再将图象上各点的横坐标缩短到原来的(纵坐标不变)D.先将的图象向左平移个单位长度,再将图象上各点的横坐标缩短到原来的(纵坐标不变)11.已知是定义在上的奇函数,且,当时,,关于函数,下列说法正确的是()A.为偶函数B.在(1,2)上单调递增C.在[2016,2020]上恰有三个零点D.的最大值为212.已知函数f(x)=e|x|sinx,下列说法正确的是()A.f(x)是周期为2π的奇函数B.f(x)在(-,)上为增函数C.f(x)在(-10π,10π)内有21个极值点D.f(x)≥ax在[0,]上恒成立的充要条件是a≤1三、填空题(每题5分,满分20分。)13.已知向量,向量,则__________.14.已知,,且,若不等式恒成立,则的取值范围是__________.15.设锐角三角形的内角所对的边分别为,若,则的取值范围为__________.16.我国著名的数学家秦九韶在《数书九章》提出了“三斜求积术”.他把三角形的三条边分别称为小斜、中斜和大斜.三斜求积术就是用小斜平方加上大斜平方,送到中斜平方,取相减后余数的一半,自乘而得一个数,小斜平方乘以大斜平方,送到上面得到的那个数,相减后余数被4除,所得的数作为“实”,1作为“隅”,开平方后即得面积.所谓“实”、“隅”指的是在方程中,为“隅”,为“实”.即若的大斜、中斜、小斜分别为,则.已知点是边上一点,则的面积为____________.四、解答题(本大题共5小题,共70分。解答应写出文字说明、证明过程或演算步骤。)17.(满分10分)在①,②,③这三个条件中任选一个,补充在下面问题中.若问题中的三角形存在,求的值;若问题中的三角形不存在,说明理由.问题:是否存在,它的内角,,的对边分别为,,,__________,且,?注:如果选择多个条件解答,按第一个解答计分.18(满分12分)(1)已知,求的值.(2)已知角的终边过点,为第三象限角,且,求的值.19.(满分12分)在中,、、分别是角、、的对边,且.(1)求角的值;(2)若,且为锐角三角形,求的取值范围.20.(满分12分)已知函数f(x)=lnx﹣x2﹣ax.(Ⅰ)当a=1时,求曲线y=f(x)则x=1处的切线方程;(Ⅱ)若f(x)≤0恒成立,求a的取值范围.21.已知函数f(x)=ex﹣x﹣a(a∈R).(1)当a=0时,求证:f(x)>x;(2)讨论函数f(x)在R上的零点个数,并求出相对应的a的取值范围.22.已知函数f(x)=-x+alnx.(1)讨论f(x)的单调性;(2)若f(x)存在两个极值点x1,x2,求证: