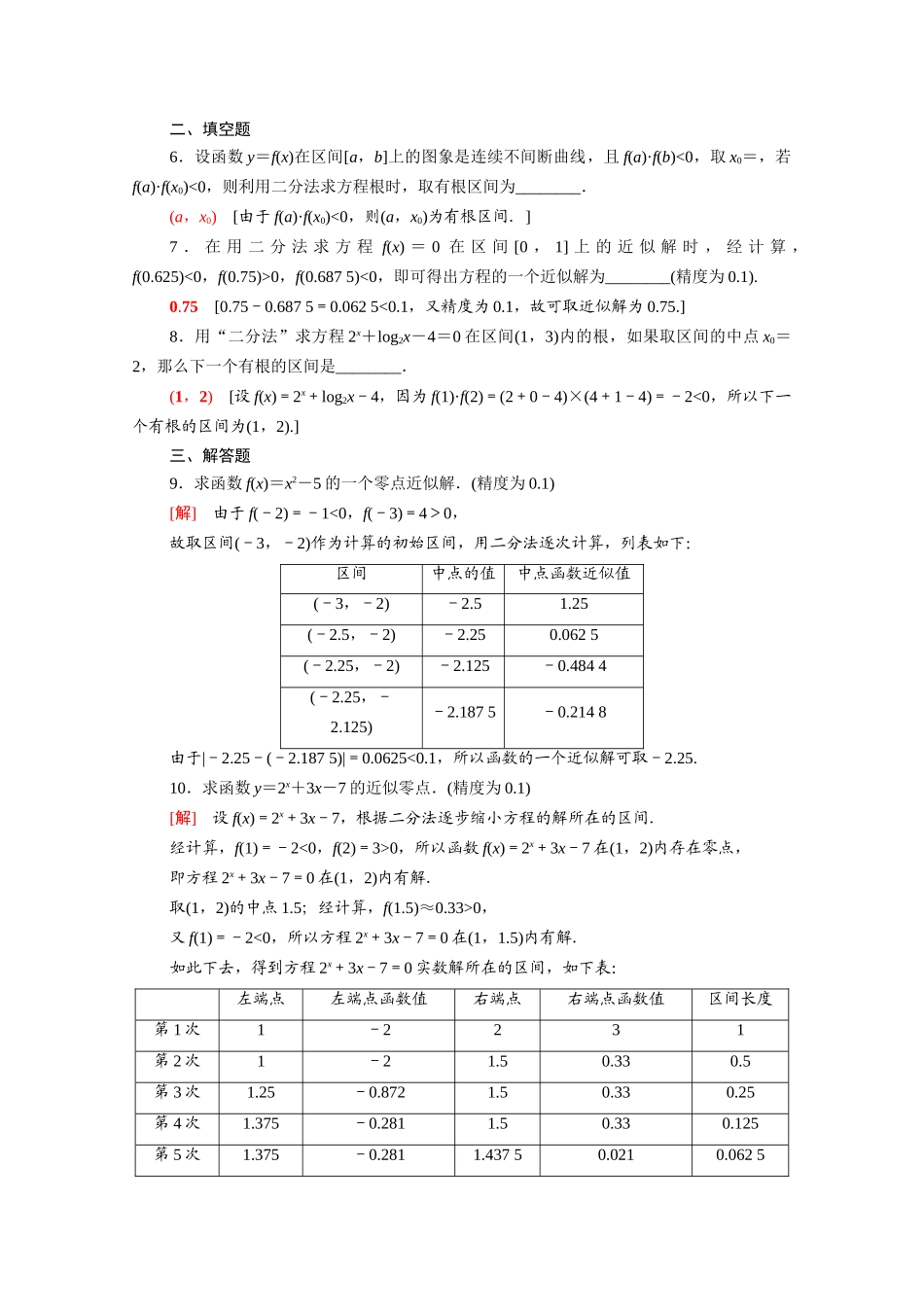
课时分层作业(三十)利用二分法求方程的近似解(建议用时:40分钟)一、选择题1.用二分法求如图所示的函数f(x)的零点时,不可能求出的零点是()A.x1B.x2C.x3D.x4C[能用二分法求零点的函数必须满足在区间[a,b]上连续,且f(a)f(b)<0.而x3两边的函数值都小于零,不符合二分法求零点的条件,故选C.]2.用“二分法”可求近似解,对于精度ε说法正确的是()A.ε越大,零点的精度越高B.ε越大,零点的精度越低C.重复计算次数就是εD.重复计算次数与ε无关B[依“二分法”的具体步骤可知,ε越大,零点的精度越低.]3.设f(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得f(1)<0,f(1.5)>0,f(1.25)<0,则方程3x+3x-8=0的根落在区间()A.(1.25,1.5)B.(1,1.25)C.(1.5,2)D.不能确定A[易知f(x)在R上是增函数.由题意可知f(1.25)·f(1.5)<0,故函数f(x)=3x+3x-8的零点落在区间(1.25,1.5)内.故选A.]4.用二分法求方程lnx-=0的零点时,初始区间大致可选在()A.(1,2)B.(2,3)C.(3,4)D.(e,+∞)B[设f(x)=lnx-,由于f(2)=ln2-1<0,f(3)=ln3->0,f(2)·f(3)<0,故初始区间可选(2,3).]5.用二分法求函数f(x)=2x+3x-7在区间[0,4]上的零点近似值,取区间中点2,则下一个存在零点的区间为()A.(0,1)B.(0,2)C.(2,3)D.(2,4)B[因为f(0)=20+0-7=-6<0,f(4)=24+12-7>0,f(2)=22+6-7>0,所以f(0)·f(2)<0,所以零点在区间(0,2)内.]二、填空题6.设函数y=f(x)在区间[a,b]上的图象是连续不间断曲线,且f(a)·f(b)<0,取x0=,若f(a)·f(x0)<0,则利用二分法求方程根时,取有根区间为________.(a,x0)[由于f(a)·f(x0)<0,则(a,x0)为有根区间.]7.在用二分法求方程f(x)=0在区间[0,1]上的近似解时,经计算,f(0.625)<0,f(0.75)>0,f(0.6875)<0,即可得出方程的一个近似解为________(精度为0.1).0.75[0.75-0.6875=0.0625<0.1,又精度为0.1,故可取近似解为0.75.]8.用“二分法”求方程2x+log2x-4=0在区间(1,3)内的根,如果取区间的中点x0=2,那么下一个有根的区间是________.(1,2)[设f(x)=2x+log2x-4,因为f(1)·f(2)=(2+0-4)×(4+1-4)=-2<0,所以下一个有根的区间为(1,2).]三、解答题9.求函数f(x)=x2-5的一个零点近似解.(精度为0.1)[解]由于f(-2)=-1<0,f(-3)=4>0,故取区间(-3,-2)作为计算的初始区间,用二分法逐次计算,列表如下:区间中点的值中点函数近似值(-3,-2)-2.51.25(-2.5,-2)-2.250.0625(-2.25,-2)-2.125-0.4844(-2.25,-2.125)-2.1875-0.2148由于|-2.25-(-2.1875)|=0.0625<0.1,所以函数的一个近似解可取-2.25.10.求函数y=2x+3x-7的近似零点.(精度为0.1)[解]设f(x)=2x+3x-7,根据二分法逐步缩小方程的解所在的区间.经计算,f(1)=-2<0,f(2)=3>0,所以函数f(x)=2x+3x-7在(1,2)内存在零点,即方程2x+3x-7=0在(1,2)内有解.取(1,2)的中点1.5;经计算,f(1.5)≈0.33>0,又f(1)=-2<0,所以方程2x+3x-7=0在(1,1.5)内有解.如此下去,得到方程2x+3x-7=0实数解所在的区间,如下表:左端点左端点函数值右端点右端点函数值区间长度第1次1-2231第2次1-21.50.330.5第3次1.25-0.8721.50.330.25第4次1.375-0.2811.50.330.125第5次1.375-0.2811.43750.0210.0625由表可以看出,区间(1.375,1.4375)内的所有值都可以看成是函数精度为0.1时的近似零点.所以函数y=2x+3x-7的一个近似零点可以是1.411.若函数f(x)在(1,2)内有1个零点,要使零点的近似值满足精度为0.01,则对区间(1,2)至少二等分()A.5次B.6次C.7次D.8次C[设对区间(1,2)至少二等分n次,初始区间长为1.第1次二等分后区间长为;第2次二等分后区间长为;第3次二等分后区间长为;…;第n次二等分后区间长为.根据题意,得<0.01,∴n>log2100. 60,f(2)=log32-=log32-log33=log3=log3<0,f=log3...