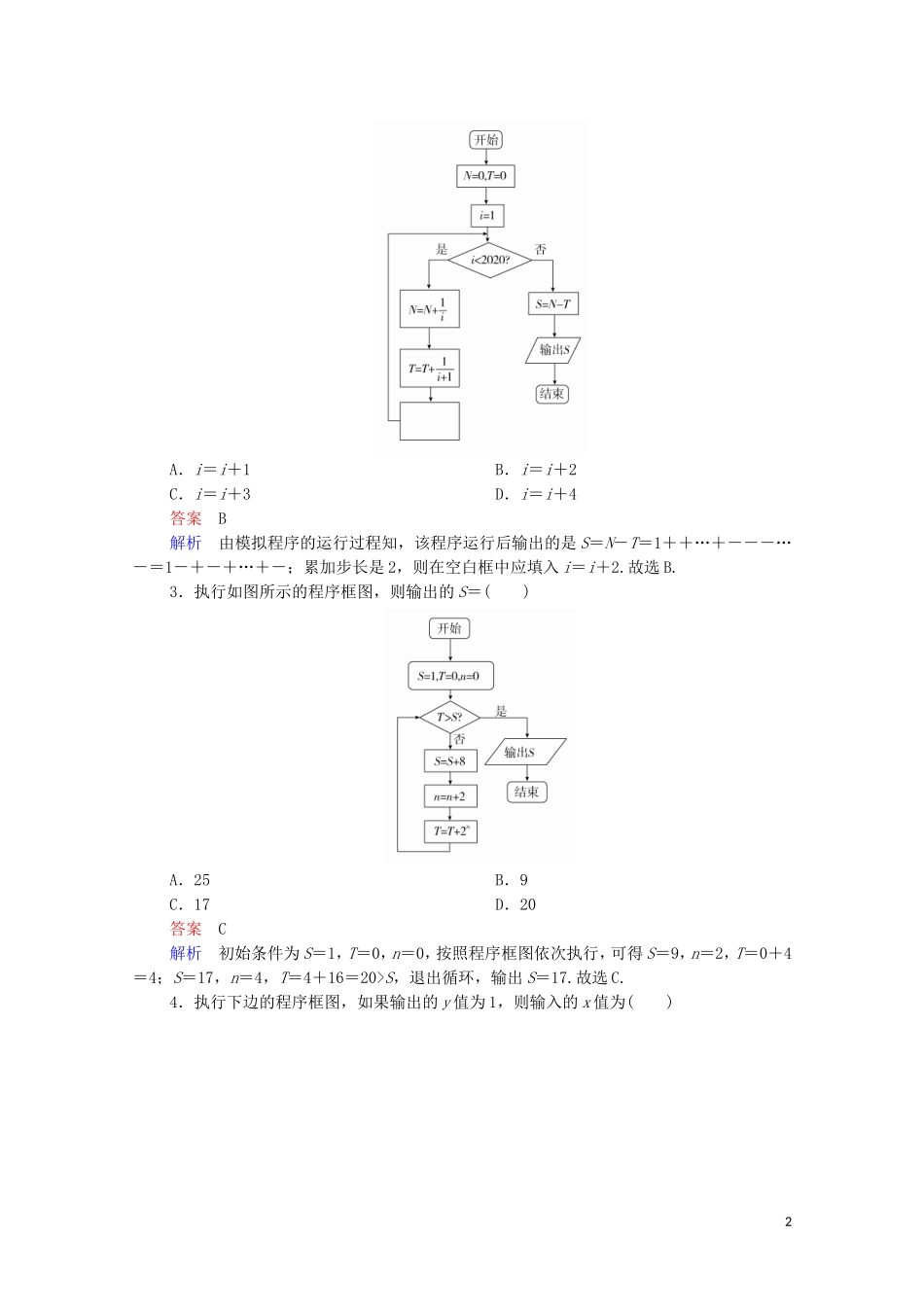
考点测试38算法初步高考概览本考点是高考必考知识点,常考题型为选择题、填空题,分值5分,中、低等难度考纲研读1.了解算法的含义,了解算法的思想2.理解程序框图的三种基本逻辑结构:顺序、条件、循环3.了解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义一、基础小题1.图中所示的程序的作用是()INPUTA,BX=AA=BB=XPRINTA,BENDA.输出两个变量A和B的值B.把变量A的值赋给变量B,并输出A和B的值C.把变量B的值赋给变量A,并输出A和B的值D.交换两个变量A和B的值,并输出交换后的值答案D解析模拟程序的运行,可得该程序的作用是交换两个变量A和B的值,并输出交换后的值.故选D.2.为了计算S=1-+-+…+-,设计如图所示的程序框图,则在空白框中应填入()1A.i=i+1B.i=i+2C.i=i+3D.i=i+4答案B解析由模拟程序的运行过程知,该程序运行后输出的是S=N-T=1++…+---…-=1-+-+…+-;累加步长是2,则在空白框中应填入i=i+2.故选B.3.执行如图所示的程序框图,则输出的S=()A.25B.9C.17D.20答案C解析初始条件为S=1,T=0,n=0,按照程序框图依次执行,可得S=9,n=2,T=0+4=4;S=17,n=4,T=4+16=20>S,退出循环,输出S=17.故选C.4.执行下边的程序框图,如果输出的y值为1,则输入的x值为()2A.0B.eC.0或eD.0或1答案C解析程序对应的函数为y=若x≤0,由y=1,得ex=1,得x=0,满足条件;若x>0,由y=2-lnx=1,得lnx=1,即x=e,满足条件.综上,输入的x值为0或e,故选C.5.右面的程序框图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的()A.c>x?B.x>c?C.c>b?D.b>c?答案A解析由流程图可知a,b,c中的最大数用变量x表示并输出,先将a的值赋给变量x.第一个判断框是判断x与b的大小关系,若b>x,则将b的值赋给变量x,得到x的值是a,b中的较大者.∴第二个判断框一定是判断a,b中的较大者x与c的大小关系,并将最大数赋给变量x,故第二个判断框内应填入c>x?.6.执行如图所示的程序框图,则输出的x等于()3A.16B.8C.4D.2答案B解析执行一次循环体y=-2,x=2;执行两次循环体y=3,x=4;执行三次循环体y=1,x=8,此时输出x=8.故选B.7.根据如图算法语句,当输入x的值为60时,输出y的值为()A.25B.30C.31D.61答案C解析当x=60时,y=25+0.6×10=31.故选C.8.执行如图所示的程序框图,若输入x的值为3,则输出的x的值是()A.6B.21C.156D.231答案D解析执行一次循环体x=6<100,执行二次循环体x=21<100,执行三次循环体x=231>100,此时输出231,故选D.9.阅读如图所示的程序框图,该算法的功能是()4A.计算(1+20)+(2+21)+(3+22)+…+(n+1+2n)的值B.计算(1+21)+(2+22)+(3+23)+…+(n+2n)的值C.计算(1+2+3+…+n)+(20+21+22+…+2n-1)的值D.计算[1+2+3+…+(n-1)]+(20+21+22+…+2n)的值答案C解析初始值k=1,S=0,第1次进入循环体时,S=1+20,k=2;第2次进入循环体时,S=1+20+2+21,k=3;第3次进入循环体时,S=1+20+2+21+3+22,k=4;…;给定正整数n,当k=n时,最后一次进入循环体,则有S=1+20+2+21+…+n+2n-1,k=n+1,终止循环体,输出S=(1+2+3+…+n)+(20+21+22+…+2n-1).10.如图是某算法的程序框图,则程序运行后输出的n是()A.168B.169C.337D.338答案C解析初始值n=0,k=1,开始循环,sin=,n=1,k=2;sin=,n=1,k=3;sin=1,n=1,k=4;sin=,n=1,k=5;sin=,n=2,k=6;sin=0,n=2,k=7;sin=-,n=2,k=8;sin=-,n=2,k=9;sin=-1,n=2,k=10;sin=-,n=2,k=11;sin=-,n=2,k=12;sin=0,n=2,k=13;…;由此可知sin的值是以12为周期出现的,又2019=12×168+3,所以输出5的n的值为168×2+1=337,故选C.11.计算机在处理数据时使用的是二进制,例如十进制数1,2,3,4的二进制数分别表示为1,10,11,100,二进制数…dcba化为十进制数的公式为…dcba=a·20+b·21+c·22+d·23+…...