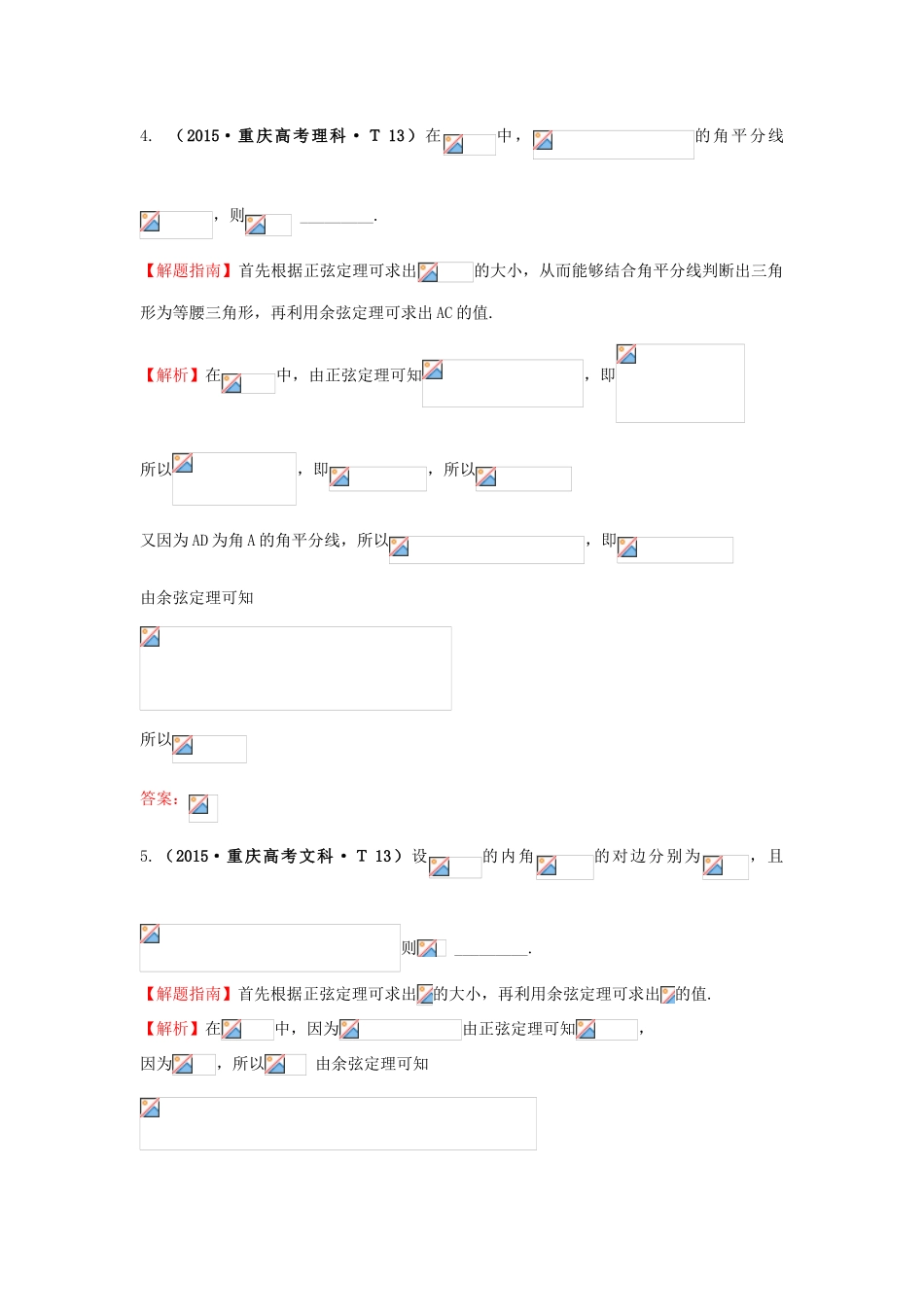
考点17解三角形应用举例填空题:1.(2015·新课标全国卷Ⅰ理科·T16)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围.【解析】如图所示,延长BA,CD交于点E,可知在△ADE中,∠DAE=105°,∠ADE=45°,∠E=30°.设,,.设,由,得,得,所以.而,所以的取值范围是.答案:2.(2015·湖北高考理科·T13)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=m.【解题指南】先用正弦定理求得BC的长度,再解三角形得出CD的长度.【解析】在△ABC中,∠CAB=30°,∠ACB=75°-30°=45°,根据正弦定理知,=,即所以(m).答案:3.(2015·湖北高考文科·T15)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=m.【解题指南】先用正弦定理求得BC的长度,再解三角形得出CD的长度.【解析】在△ABC中,∠CAB=30°,∠ACB=75°-30°=45°,根据正弦定理知,=,即所以(m).答案:4.(2015·重庆高考理科·T13)在中,的角平分线,则_________.【解题指南】首先根据正弦定理可求出的大小,从而能够结合角平分线判断出三角形为等腰三角形,再利用余弦定理可求出AC的值.【解析】在中,由正弦定理可知,即所以,即,所以又因为AD为角A的角平分线,所以,即由余弦定理可知所以答案:5.(2015·重庆高考文科·T13)设的内角的对边分别为,且则_________.【解题指南】首先根据正弦定理可求出的大小,再利用余弦定理可求出的值.【解析】在中,因为由正弦定理可知,因为,所以由余弦定理可知所以答案: