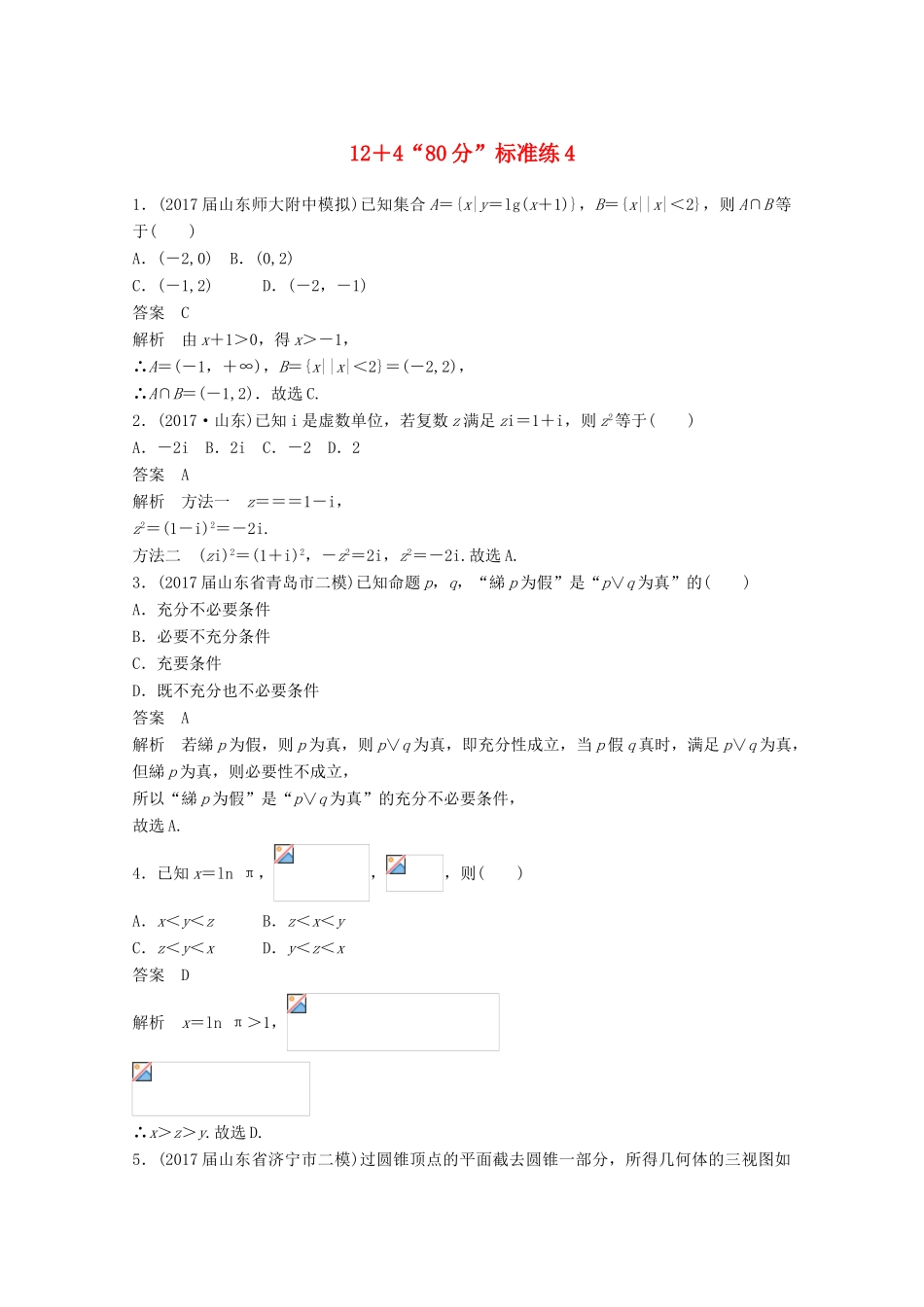
12+4“80分”标准练41.(2017届山东师大附中模拟)已知集合A={x|y=lg(x+1)},B={x||x|<2},则A∩B等于()A.(-2,0)B.(0,2)C.(-1,2)D.(-2,-1)答案C解析由x+1>0,得x>-1,∴A=(-1,+∞),B={x||x|<2}=(-2,2),∴A∩B=(-1,2).故选C.2.(2017·山东)已知i是虚数单位,若复数z满足zi=1+i,则z2等于()A.-2iB.2iC.-2D.2答案A解析方法一z===1-i,z2=(1-i)2=-2i.方法二(zi)2=(1+i)2,-z2=2i,z2=-2i.故选A.3.(2017届山东省青岛市二模)已知命题p,q,“綈p为假”是“p∨q为真”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案A解析若綈p为假,则p为真,则p∨q为真,即充分性成立,当p假q真时,满足p∨q为真,但綈p为真,则必要性不成立,所以“綈p为假”是“p∨q为真”的充分不必要条件,故选A.4.已知x=lnπ,,,则()A.x<y<zB.z<x<yC.z<y<xD.y<z<x答案D解析x=lnπ>1,∴x>z>y.故选D.5.(2017届山东省济宁市二模)过圆锥顶点的平面截去圆锥一部分,所得几何体的三视图如图所示,则原圆锥的体积为()A.1B.C.D.答案D解析由三视图可得底面圆的半径为=2,圆锥的高为=2,∴原圆锥的体积为π·22·2=,故选D.6.(2017届广东省深圳市二模)一个三位数,个位、十位、百位上的数字依次为x,y,z,当且仅当y>x,y>z时,称这样的数为“凸数”(如243),现从集合{1,2,3,4}中取出三个不相同的数组成一个三位数,则这个三位数是“凸数”的概率为()A.B.C.D.答案B解析在{1,2,3,4}的4个整数中任取3个不同的数组成三位数,有24种情况,在{1,2,3,4}的4个整数中任取3个不同的数,将最大的放在十位上,剩余的2个数字分别放在百、个位上,有8种情况,则这个三位数是“凸数”的概率是=.故选B.7.(2017届安徽省合肥市三模)《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的节气(小暑)晷长为()A.五寸B.二尺五寸C.三尺五寸D.一丈二尺五寸答案A解析设晷长为等差数列{an},公差为d,a1=135,a13=15,则135+12d=15,解得d=-10.∴a14=135-10×13=5,∴夏至之后的节气(小暑)的晷长是5寸.故选A.8.(2017届江西省重点中学联考)元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,则一开始输入的x的值为()A.B.C.D.4答案B解析i=1时,x=2x-1,i=2时,x=2(2x-1)-1=4x-3,i=3时,x=2(4x-3)-1=8x-7,i=4时,退出循环,此时8x-7=0,解得x=,故选B.9.(2017届山东省青岛市二模)已知函数f(x)=sin-cos2x+(x∈R),则下列说法正确的是()A.函数f(x)的最小正周期为B.函数f(x)的图象关于y轴对称C.点为函数f(x)图象的一个对称中心D.函数f(x)的最大值为答案D解析函数f(x)=sin-cos2x+=-+=sin2x+cos2x=sin(x∈R),由ω=2知,f(x)的最小正周期为π,A错误; f(0)=sin=不是最值,∴f(x)的图象不关于y轴对称,B错误; f=sin=≠0,∴点不是函数f(x)图象的一个对称中心,C错误; sin∈[-1,1],∴f(x)的最大值是,D正确.故选D.10.(2017届山东省、湖北省部分重点中学模拟)已知实数x,y满足不等式组若目标函数z=y-mx取得最大值时有唯一的最优解(1,3),则实数m的取值范围是()A.m<-1B.0<m<1C.m>1D.m≥1答案C解析作出不等式组对应的平面区域如图,由z=y-mx,得y=mx+z,即直线的截距最大,z也最大,若m=0,此时y=z,不满足条件;若m>0,目标函数y=mx+z的斜率k=m>0,要使目标函数z=y-mx取得最大值时有唯一的最优解(1,3),则直线y=mx+z的斜率m>1,若m<0,目标函数y=mx+z的斜率k=m<0,不满足题意.综上,m>1.故选C.11.已知双曲线C:-=1(a>0,b>0),过点P(3,6)的直线l与C相交于A,B两点,且AB的中点为N...