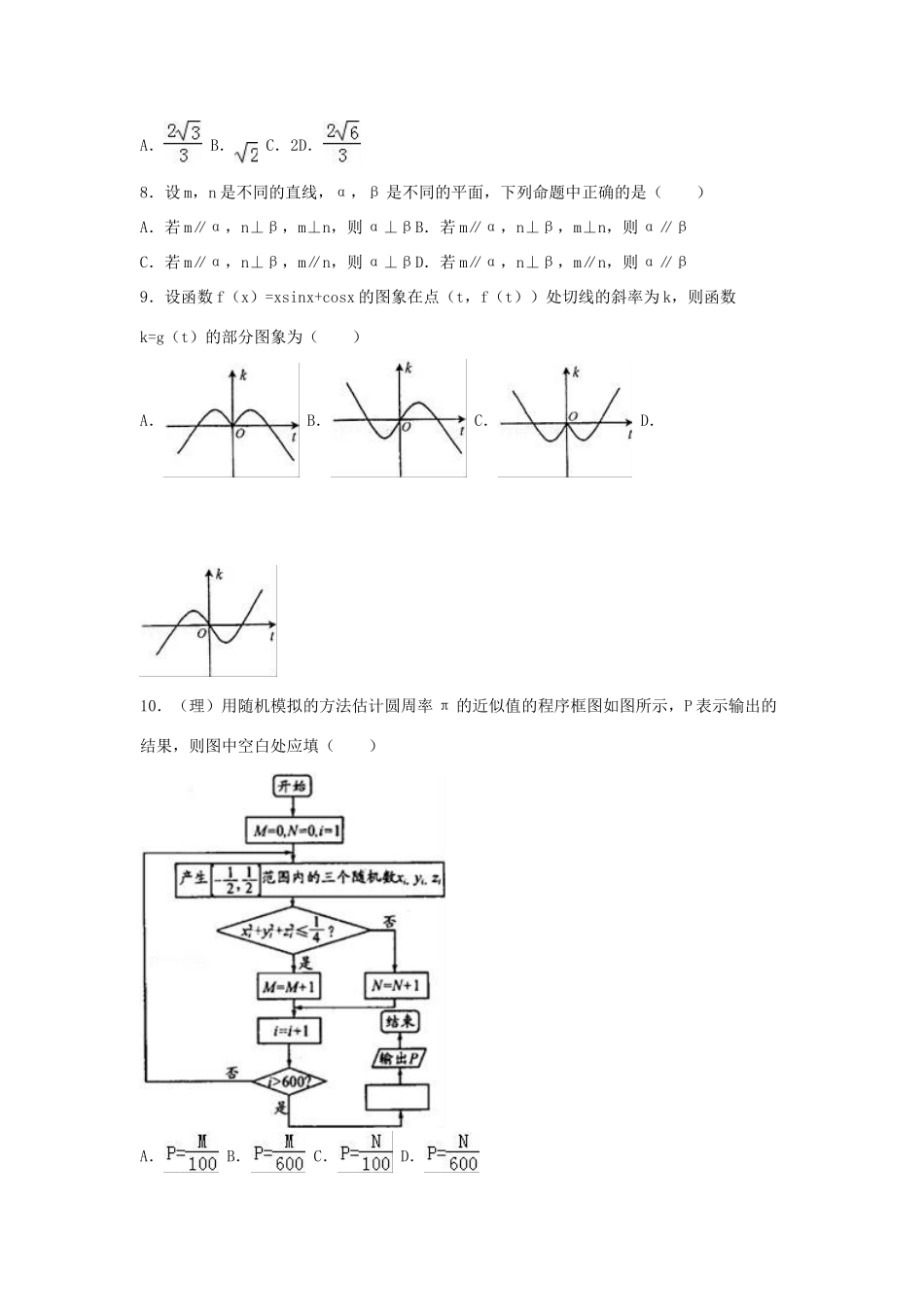
2016年辽宁省沈阳二中高考数学四模试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数z满足(3﹣4i)z=|4+3i|,则z的虚部为()A.﹣4B.C.4D.2.已知集合M={x||x﹣1|≤1},N={x|y=log2(x2﹣1)},则M∪N=()A.(1,2]B.(﹣∞,﹣1)∪[0,+∞)C.(﹣∞,0]∪[1,+∞)D.(﹣∞,﹣1)∪[0,2]3.已知向量,满足||=4,在方向上的投影是,则•=()A.﹣2B.2C.0D.4.命题“x2+y2=0,则x=y=0”的否定命题为()A.若x2+y2=0,则x≠0且y≠0B.若x2+y2=0,则x≠0或y≠0C.若x2+y2≠0,则x≠0且y≠0D.若x2+y2≠0,则x≠0或y≠05.已知b,则下列不等式一定成立的是()A.B.C.ln(a﹣b)>0D.3a﹣b>16.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今三十织迄,问织几何.”其意思为:有个女子不善于织布,每天比前一天少织同样多的布,第一天织五尺,最后一天织一尺,三十天织完,问三十天共织布()A.30尺B.90尺C.150尺D.180尺7.已知l是双曲线C:﹣=1的一条渐近线,P是l上的一点,F1,F2是C的两个焦点,若•=0,则P到x轴的距离为()A.B.C.2D.8.设m,n是不同的直线,α,β是不同的平面,下列命题中正确的是()A.若m∥α,n⊥β,m⊥n,则α⊥βB.若m∥α,n⊥β,m⊥n,则α∥βC.若m∥α,n⊥β,m∥n,则α⊥βD.若m∥α,n⊥β,m∥n,则α∥β9.设函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的部分图象为()A.B.C.D.10.(理)用随机模拟的方法估计圆周率π的近似值的程序框图如图所示,P表示输出的结果,则图中空白处应填()A.B.C.D.11.设集合M={(x,y)|(x+1)2+y2=1,x,y∈R},N={(x,y)|x+y﹣c≥0,x,y∈R},则使得M∩N=M的c的取值范围是()A.B.(﹣∞,﹣]C.[,+∞)D.(﹣∞,﹣]12.定义在(0,)上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则()A.f()>f()B.f(1)>2f()•sin1C.f()>f()D.f()>f()二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.13.已知的展开(1﹣2x)5式中所有项的系数和为m,则.14.正方体ABCD﹣A1B1C1D1的棱长为8,P、Q分别是棱A1B1和B1C1的中点,则点A1到平面APQ的距离为.15.以下命题正确的是.①函数y=3sin(2x+)的图象向右平移个单位,可得到y=3sin2x的图象;②函数f(x)=x+(x>0)的最小值为2;③某校开设A类选修课3门,B类选择课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有30种;④在某项测量中,测量结果ξ服从正态分布N(2,σ2)(σ>0).若ξ在(﹣∞,1)内取值的概率为0.1,则ξ在(2,3)内取值的概率为0.4.16.已知数列{an}的前n项和为Sn,S1=6,S2=4,Sn>0,且S2n,S2n﹣1.S2n+2成等比数列,S2n﹣1.S2n+2,S2n+1成等差数列,则a2016等于.三、解答题(本大题包括6小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.设△ABC的内角A,B,C所对的边分别为a,b,c,已知,b=3.(Ⅰ)求角B;(Ⅱ)若sinA=,求△ABC的面积.18.根据某水文观测点的历史统计数据,得到某河流水位X(单位:米)的频率分布直方图如图:将河流水位在以上6段的频率作为相应段的概率,并假设每年河流水位互不影响(1)求未来三年,至多有1年河流水位X∈[27,31)的概率(结果用分数表示);(2)该河流对沿河A企业影响如下:当X∈[23,27)时,不会造成影响;当X∈[27,31)时,损失10000元;当X∈[31,35)时,损失60000元,为减少损失,现有种应对方案:方案一:防御35米的最高水位,需要工程费用3800元;方案二:防御不超过31米的水位,需要工程费用2000元;方案三:不采取措施;试比较哪种方案较好,并请说理由.19.已知一四棱锥P﹣ABCD的三视图如图,E是侧棱PC上的动点.(Ⅰ)求四棱锥P﹣ABCD的体积;(Ⅱ)当点E在何位置时,BD⊥AE?证明你的结论;(Ⅲ)若点E为PC的中...