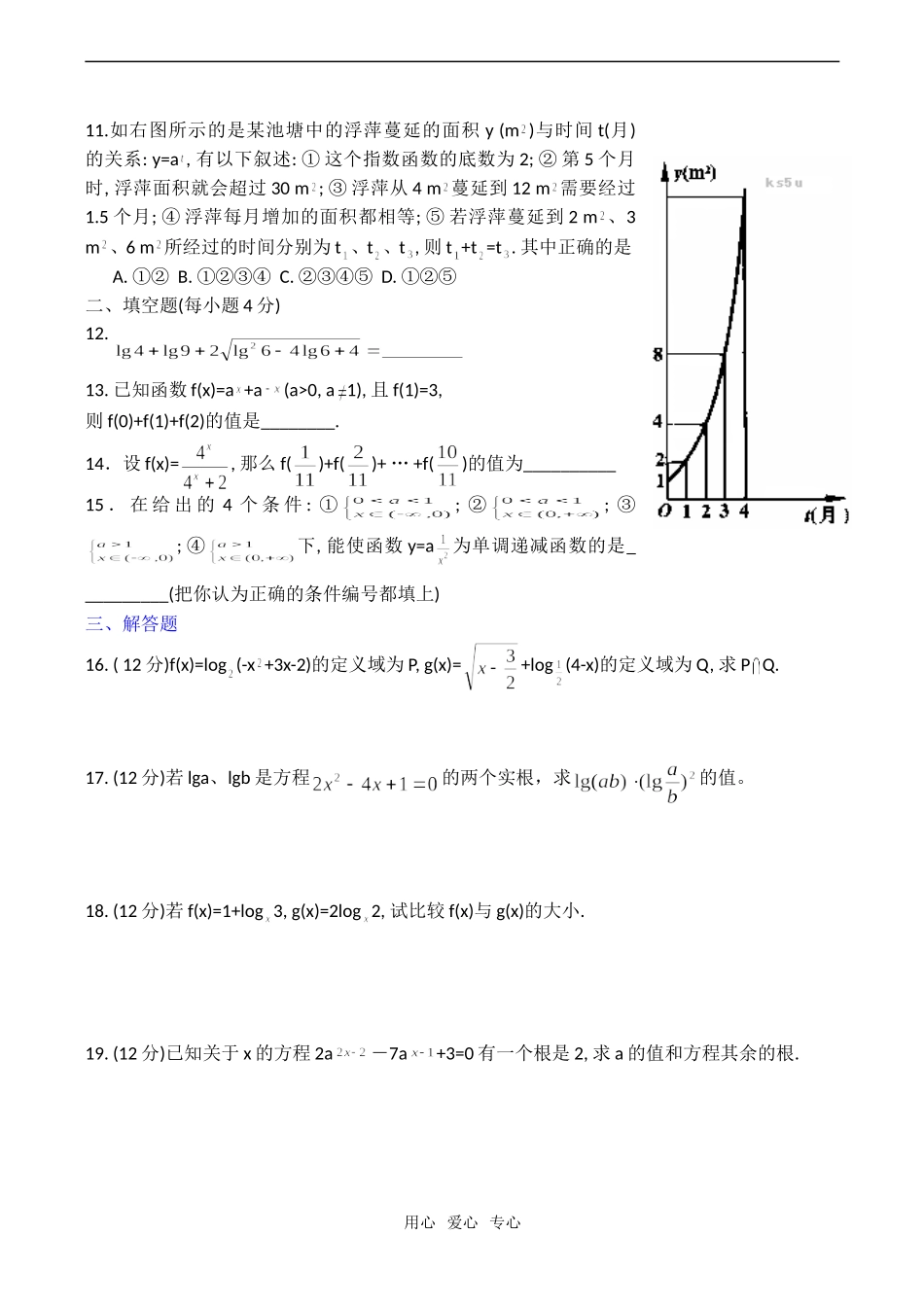
高考数学复习指数函数与对数专题训练一、选择题(每小题仅一个正确答案,答对得5分)1.设集合A和集合B都是实数集R,映射f:AB把集合A中的元素x映射到集合B中的元素lg(x+1),则在映射f下,象1的原象所成的集合是A.{-1,1}B.{3,0}C.{3,-3}D.{3}2.集合M={x|≥0},N={x|3≥1},则集合M、N的关系是A.M=NB.MNC.MND.MN3.已知ab=m(a>0,b>0,m≠1)且,则等于A.1-xB.1+xC.D.x-14.已知lga和lgb互为相反数,则有A.a+b=0B.ab=1C.=1D.不同于A,B,C5.下列函数中,值域为R的是A.y=5B.y=()C.y=D.y=6.若函数f(x)=3+2的反函数的图象过点P,则P点坐标为A.(2,5)B.(1,3)C.(5,2)D.(3,1)7.已知log3=p,log5=q,则lg5(用p、q表示)等于A.B.C.D.p+q8.当x(0,)时,下列式子中正确的是A.log(1-x)>1B.()>()C.(1+x)<(1-x)D.log(1-x)>-19.已知F(x)=(1+)·f(x)(x0)是偶函数,且f(x)不恒为零,则f(x)A.是奇函数B.是偶函数C.既是奇函数也是偶函数D.非奇非偶函数10、设a>0且a1,f(x)=-x+a,对x(-,)均有f(x)>0,则a()A.(0,[16,+B.(0,)(1,+C.[,16]且a1D.[,2]且a1用心爱心专心11.如右图所示的是某池塘中的浮萍蔓延的面积y(m)与时间t(月)的关系:y=a,有以下叙述:①这个指数函数的底数为2;②第5个月时,浮萍面积就会超过30m;③浮萍从4m蔓延到12m需要经过1.5个月;④浮萍每月增加的面积都相等;⑤若浮萍蔓延到2m、3m、6m所经过的时间分别为t、t、t,则t+t=t.其中正确的是A.①②B.①②③④C.②③④⑤D.①②⑤二、填空题(每小题4分)12.13.已知函数f(x)=a+a(a>0,a1),且f(1)=3,则f(0)+f(1)+f(2)的值是________.14.设f(x)=,那么f()+f()+…+f()的值为__________15.在给出的4个条件:①;②;③;④下,能使函数y=a为单调递减函数的是__________(把你认为正确的条件编号都填上)三、解答题16.(12分)f(x)=log(-x+3x-2)的定义域为P,g(x)=+log(4-x)的定义域为Q,求PQ.17.(12分)若lga、lgb是方程的两个实根,求的值。18.(12分)若f(x)=1+log3,g(x)=2log2,试比较f(x)与g(x)的大小.19.(12分)已知关于x的方程2a-7a+3=0有一个根是2,求a的值和方程其余的根.用心爱心专心20.(12分)已知函数f(x)=(a-a)(a>0且a1)在(-,+)上是增函数,求实数a的取值范21.(14分)设f(x)=a+mx-n(a>0且a1),而且f(m)=a-1,f(n)=a-1(mn),F(x)=f(2x)+2f(x),求:(1)f(x)的表达式;(2)F(x)的值域.参考答案一、选择题:CDABBCCDAACD二、填空题:13.4_;14.12;15.5_;16.①④_.三、解答题:17.解:P=(1,2),Q=[,4.PQ=[,318.解:,=(lga+lgb)(lga-lgb)=2[(lga+lgb)-4lgalgb]=2(4-4×)=419.解:f(x)-g(x)=log(x).(1),即0
时,f(x)>g(x)(2),即13;(2),解得00).而t=0时,y=-3故y(-3,+)用心爱心专心