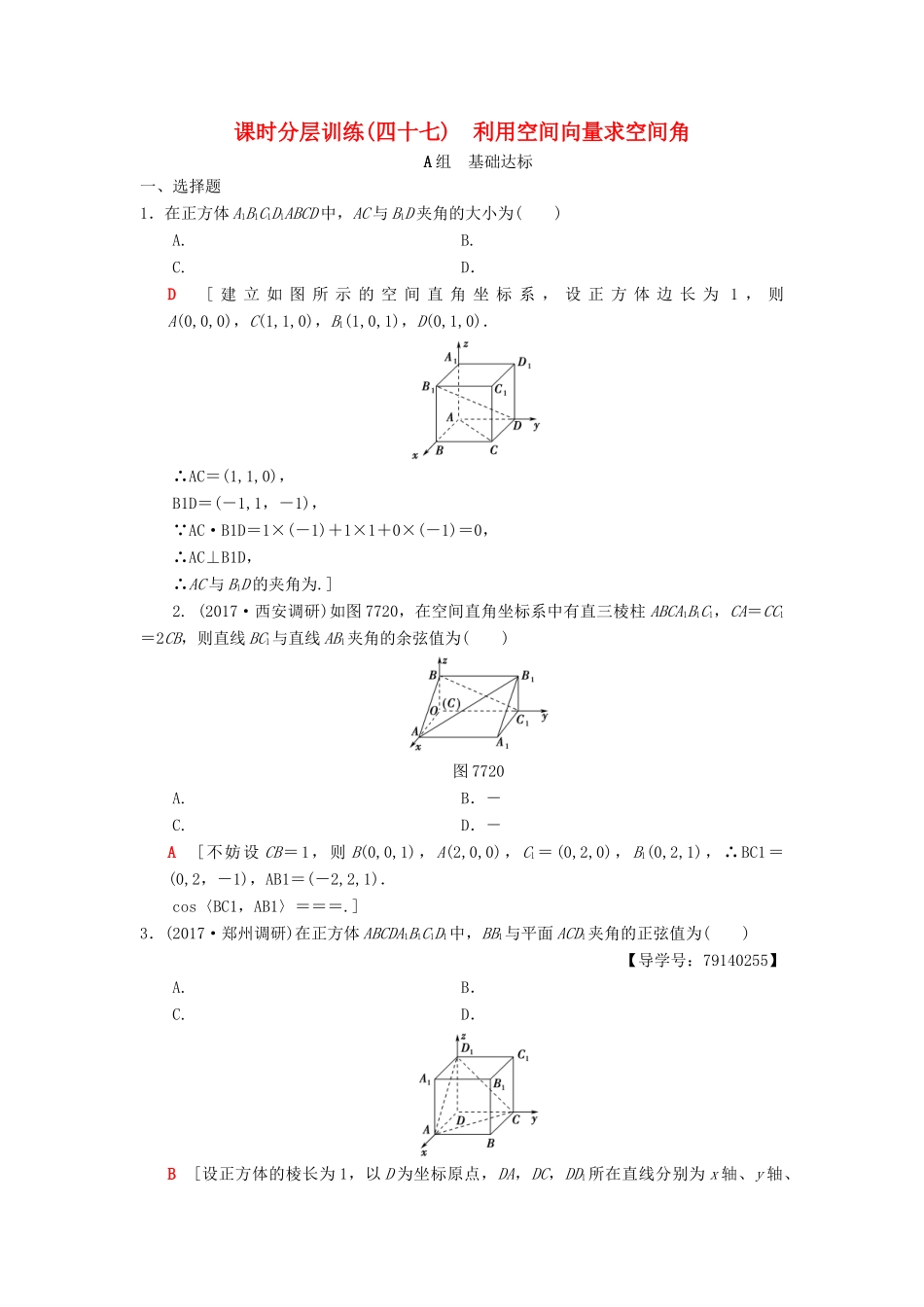
课时分层训练(四十七)利用空间向量求空间角A组基础达标一、选择题1.在正方体A1B1C1D1ABCD中,AC与B1D夹角的大小为()A.B.C.D.D[建立如图所示的空间直角坐标系,设正方体边长为1,则A(0,0,0),C(1,1,0),B1(1,0,1),D(0,1,0).∴AC=(1,1,0),B1D=(-1,1,-1), AC·B1D=1×(-1)+1×1+0×(-1)=0,∴AC⊥B1D,∴AC与B1D的夹角为.]2.(2017·西安调研)如图7720,在空间直角坐标系中有直三棱柱ABCA1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为()图7720A.B.-C.D.-A[不妨设CB=1,则B(0,0,1),A(2,0,0),C1=(0,2,0),B1(0,2,1),∴BC1=(0,2,-1),AB1=(-2,2,1).cos〈BC1,AB1〉===.]3.(2017·郑州调研)在正方体ABCDA1B1C1D1中,BB1与平面ACD1夹角的正弦值为()【导学号:79140255】A.B.C.D.B[设正方体的棱长为1,以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系,如图所示.则B(1,1,0),B1(1,1,1),A(1,0,0),C(0,1,0),D1(0,0,1),所以BB1=(0,0,1),AC=(-1,1,0),AD1=(-1,0,1).令平面ACD1的法向量为n=(x,y,z),则n·AC=-x+y=0,n·AD1=-x+z=0,令x=1,可得n=(1,1,1),所以sinθ=|cos〈n,BB1〉|==.]4.已知正三棱柱ABCA1B1C1的侧棱长与底面边长相等,则AB1与侧面ACC1A1夹角的正弦值等于()A.B.C.D.A[如图所示建立空间直角坐标系,设正三棱柱的棱长为2,则O(0,0,0),B(,0,0),A(0,-1,0),B1(,0,2),所以AB1=(,1,2),由题知BO=(-,0,0)为侧面ACC1A1的法向量.即sinθ==.故选A.]5.在正方体ABCDA1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为()A.B.C.D.B[以A为原点建立如图所示的空间直角坐标系Axyz,设棱长为1,则A1(0,0,1),E,D(0,1,0),∴A1D=(0,1,-1),A1E=.设平面A1ED的一个法向量为n1=(1,y,z),∴有即解得∴n1=(1,2,2). 平面ABCD的一个法向量为n2=(0,0,1).∴cos〈n1,n2〉==,即所成的锐二面角的余弦值为.]二、填空题6.在长方体ABCDA1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1夹角的正弦值为________.[以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设n=(x,y,z)为平面A1BC1的法向量,则n·A1B=0,n·A1C1=0,即令z=2,则y=1,x=2,于是n=(2,1,2),D1C1=(0,2,0).设所求线面角为α,则sinα=|cos〈n,D1C1〉|=.]7.如图7721所示,二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=4,AC=6,BD=8,CD=2,则该二面角的大小为________.图772160°[ CD=CA+AB+BD,∴|CD|====2.∴CA·BD=|CA|·|BD|·cos〈CA,BD〉=-24.∴cos〈CA,BD〉=-.又所求二面角与〈CA,BD〉互补,∴所求的二面角为60°.]8.在一直角坐标系中,已知A(-1,6),B(3,-8),现沿x轴将坐标平面折成60°的二面角,则折叠后A,B两点间的距离为________.【导学号:79140256】2[如图为折叠后的图形,其中作AC⊥CD,BD⊥CD,则AC=6,BD=8,CD=4,两异面直线AC,BD夹角为60°.故由AB=AC+CD+DB,得|AB|2=|AC+CD+DB|2=68,所以|AB|=2.]三、解答题9.(2018·合肥一检)如图7722,在四棱台ABCDA1B1C1D1中,AA1⊥底面ABCD,四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2.图7722(1)若M为CD的中点,求证:AM⊥平面AA1B1B;(2)求直线DD1与平面A1BD夹角的正弦值.[解](1)证明: 四边形ABCD为菱形,∠BAD=120°,连接AC,则△ACD为等边三角形,又 M为CD的中点,∴AM⊥CD,由CD∥AB得AM⊥AB. AA1⊥底面ABCD,AM底面ABCD,∴AM⊥AA1,又 AB∩AA1=A,∴AM⊥平面AA1B1B.(2) 四边形ABCD为菱形,∠BAD=120°,AB=AA1=2A1B1=2,得DM=1,AM=,∴∠AMD=∠BAM=90°,又 AA1⊥底面ABCD,∴以点A为原点,分别以AB,AM,AA1所在直线为x轴、y轴、z轴,建立如图所示的空间直角坐标系Axyz,A1(0,0,2),B(2,0,0),D(-1,,0),D1,∴DD1=,BD=(-3,,0),A1B=(2,0,-2).设平面A1BD的法向量为n=(x,y,z),则有⇒令x=1,则n=(1,,1).∴直线DD1与平面A1BD夹角...