高中数学 第二章 点、直线、平面之间的位置关系 2.3.3-2.3.4 直线与平面垂直的性质、平面与平面垂直的性质课堂达标练 新人教A版必修2-新人教A版高一必修2数学试题VIP免费

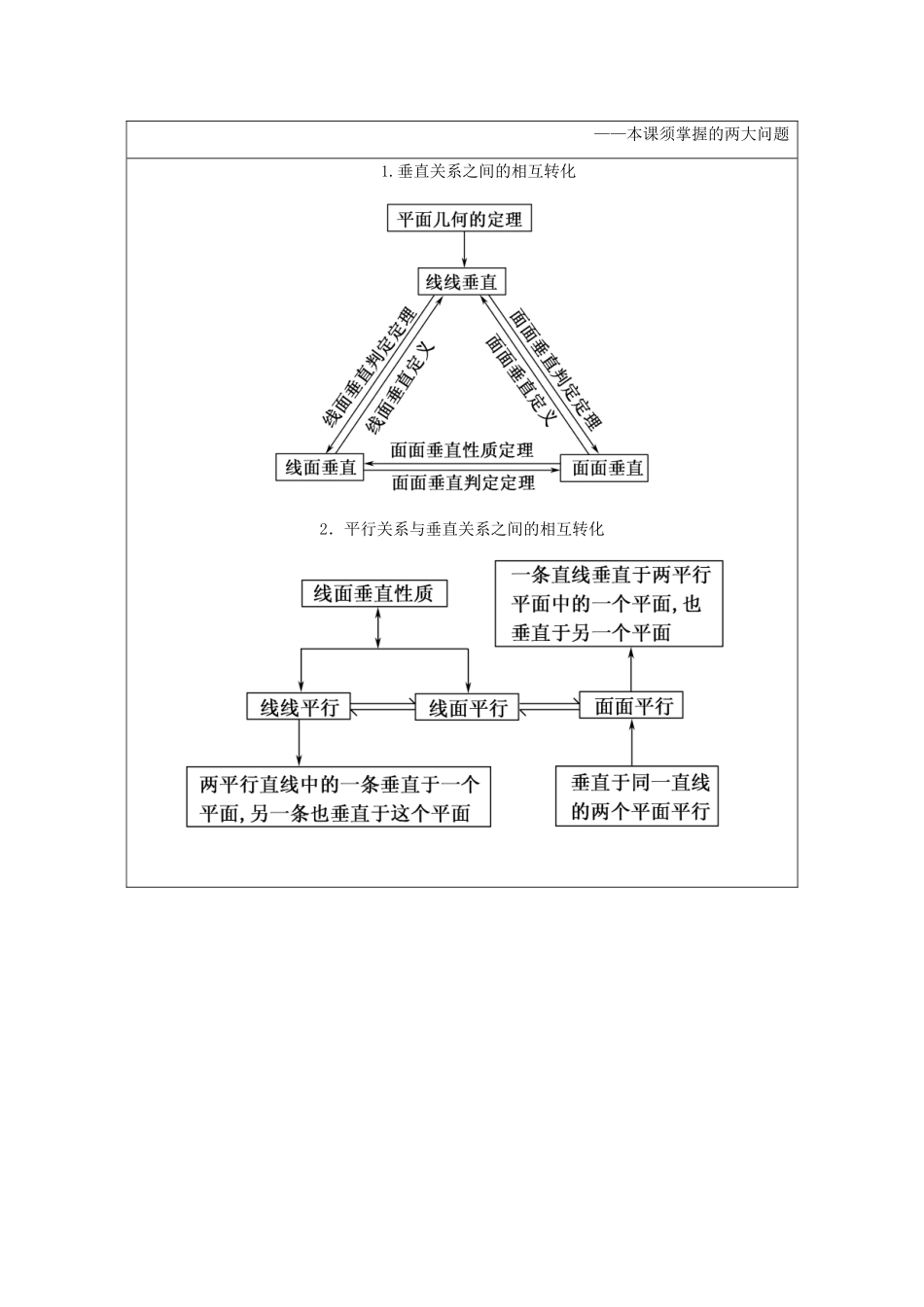
第二章点、直线、平面之间的位置关系2.3.3-2.3.4直线与平面垂直的性质、平面与平面垂直的性质课堂达标练新人教A版必修21．已知直线a，b，平面α，且a⊥α，下列条件中，能推出a∥b的是()A．b∥αB．bαC．b⊥αD．b∩α＝A答案：C2．△ABC所在的平面为α，直线l⊥AB，l⊥AC，直线m⊥BC，m⊥AC，则直线l，m的位置关系是()A．相交B．异面C．平行D．不确定解析：因为l⊥AB，l⊥AC，ABα，ACα且AB∩AC＝A，所以l⊥α，同理可证m⊥α，所以l∥m.答案：C3．设α－l－β是直二面角，直线aα，直线bβ，a，b与l都不垂直，那么()A．a与b可能垂直，但不可能平行B．a与b可能垂直，也可能平行C．a与b不可能垂直，但可能平行D．a与b不可能垂直，也不可能平行解析：当a，b都与l平行时，则a∥b，所以A、D错，如图，若a⊥b，过a上一点P在α内作a′⊥l，因为α⊥β，所以a′⊥β，又bβ，∴a′⊥b，∴b⊥α，而lα，∴b⊥l，与b和l不垂直矛盾，所以B错．答案：C4．如图，在三棱锥P－ABC内，侧面PAC⊥底面ABC，且∠PAC＝90°，PA＝1，AB＝2，则PB＝________.解析：∵侧面PAC⊥底面ABC，交线为AC，∠PAC＝90°(即PA⊥AC)，∴PA⊥平面ABC，∴PA⊥AB，∴PB＝＝＝.答案：5．已知α⊥γ，β⊥γ，α∩β＝l.求证：l⊥γ.证明：方法1：在γ内取一点P，作PA垂直α与γ的交线于A，PB垂直β与γ的交线于B，则PA⊥α，PB⊥β.∵l＝α∩β，∴l⊥PA，l⊥PB.又PA∩PB＝P，且PAγ，PBγ，∴l⊥γ.\s\up7()方法2：在α内作直线m垂直于α与γ的交线，在β内作直线n垂直于β与γ的交线，∵α⊥γ，β⊥γ，∴m⊥γ，n⊥γ.∴m∥n.又nβ，∴m∥β.又mα，α∩β＝l，∴m∥l.∴l⊥γ.课堂小结——本课须掌握的两大问题1.垂直关系之间的相互转化2．平行关系与垂直关系之间的相互转化