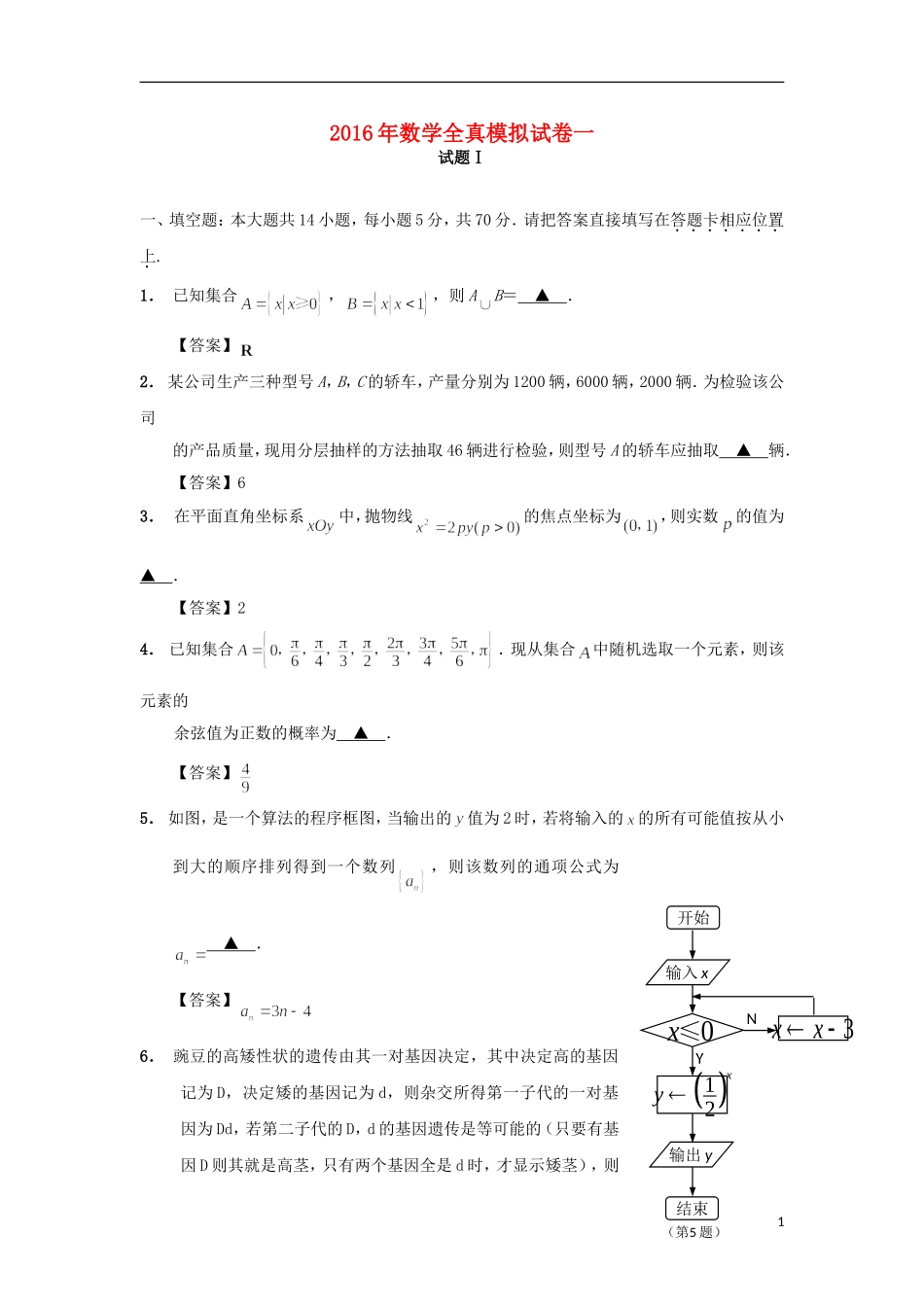
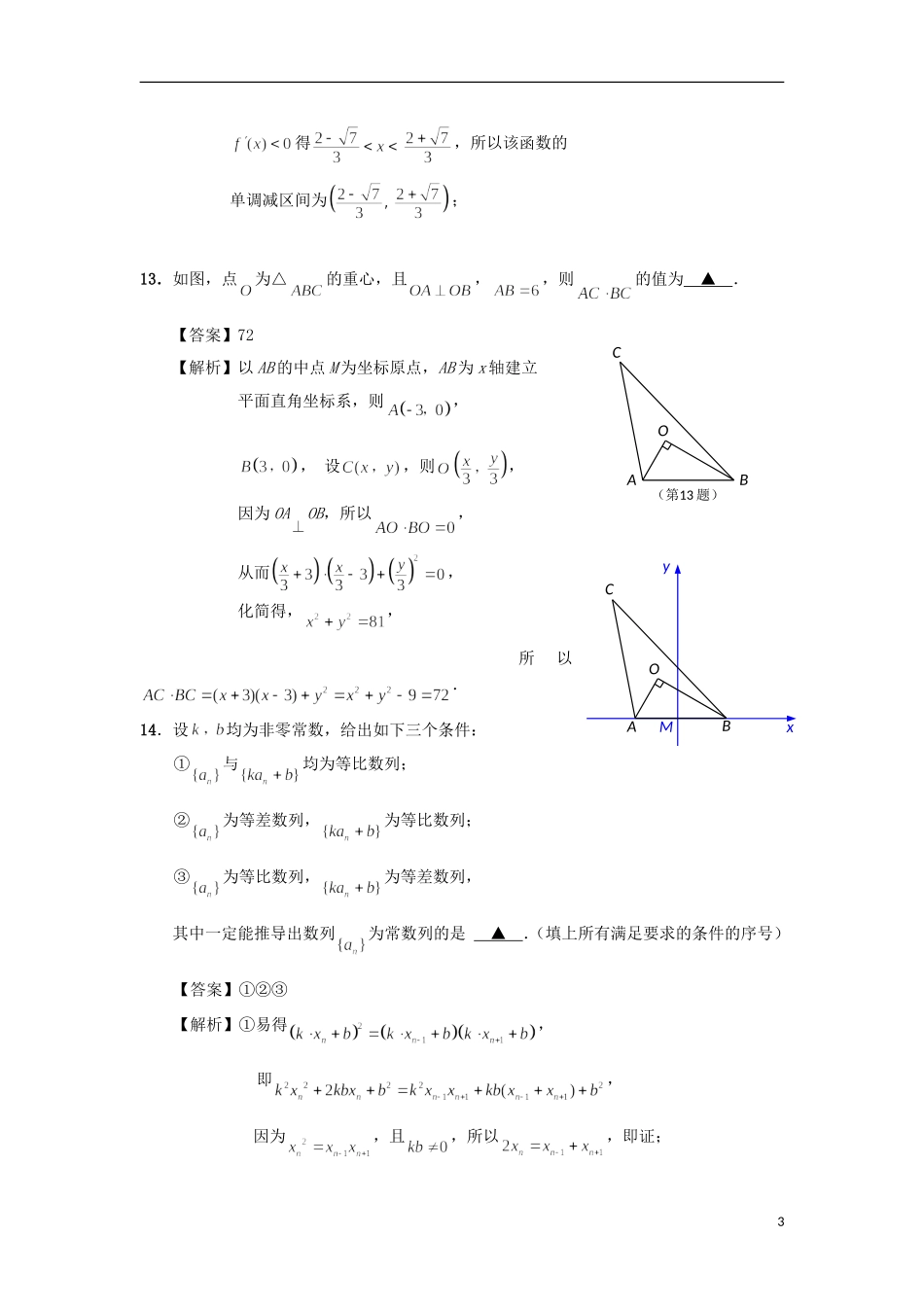
N3xx开始输入x0x≤12xy输出y结束Y(第5题)2016年数学全真模拟试卷一试题Ⅰ一、填空题:本大题共14小题,每小题5分,共70分.请把答案直接填写在答题卡相应位置上.1.已知集合,,则AB=▲.【答案】2.某公司生产三种型号A,B,C的轿车,产量分别为1200辆,6000辆,2000辆.为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,则型号A的轿车应抽取▲辆.【答案】63.在平面直角坐标系中,抛物线的焦点坐标为,则实数的值为▲.【答案】24.已知集合.现从集合中随机选取一个元素,则该元素的余弦值为正数的概率为▲.【答案】5.如图,是一个算法的程序框图,当输出的值为2时,若将输入的的所有可能值按从小到大的顺序排列得到一个数列,则该数列的通项公式为▲.【答案】6.豌豆的高矮性状的遗传由其一对基因决定,其中决定高的基因记为D,决定矮的基因记为d,则杂交所得第一子代的一对基因为Dd,若第二子代的D,d的基因遗传是等可能的(只要有基因D则其就是高茎,只有两个基因全是d时,才显示矮茎),则1ACD1B1A1C1D(第9题)EF第二子代为高茎的概率为▲.【答案】7.在平面直角坐标系xOy中,已知向量,,则▲.【答案】258.已知为正实数,满足,则的最小值为▲.【答案】189.如图,已知正四棱柱的体积为36,点,分别为棱,上的点(异于端点),且,则四棱锥的体积为▲.【答案】1210.设定义在区间的函数(其中)是偶函数,则函数的单调减区间为▲.【答案】【解析】依题意,,则的减区间为.11.在平面直角坐标系中,已知圆:,直线:.若动圆总在直线的下方且它们至多有1个交点,则实数的最小值是▲.【答案】2【解析】依题意,圆心的轨迹为线段,当且仅当,且时,实数的最小,此时.12.如图,三次函数的零点为,则该函数的单调减区间为▲.【答案】【解析】设,其中,令2(第12题)112OxyxMyBOACABCO(第13题)得,所以该函数的单调减区间为;13.如图,点为△的重心,且,,则的值为▲.【答案】72【解析】以AB的中点M为坐标原点,AB为x轴建立平面直角坐标系,则,,设,则,因为OAOB,所以,从而,化简得,,所以.14.设均为非零常数,给出如下三个条件:①与均为等比数列;②为等差数列,为等比数列;③为等比数列,为等差数列,其中一定能推导出数列为常数列的是▲.(填上所有满足要求的条件的序号)【答案】①②③【解析】①易得,即,因为,且,所以,即证;3②由①知,因为,所以,即证;③易得,且,故,又,即证.二、解答题:本大题共6小题,共90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.15.(本题满分14分)已知,,,.(1)求的值;(2)求的值.解:(1)因为,且,所以,解得,(4分)因为,所以,从而,所以.(6分)(2)因为,,所以,(8分)又,故,从而,(10分)4所以.(14分)16.(本题满分14分)如图,在长方体中,已知,,点E是AB的中点.(1)求三棱锥的体积;(2)求证:.【解】(1)由长方体性质可得,平面DEC,所以是三棱锥的高,又点E是AB的中点,,AB=2,所以,,,三棱锥的体积;(7分)(2)连结,因为是正方形,所以,又面,面,所以,又,平面,所以平面,(12分)而平面,5AEBCDAAAA(第16题)所以.(14分)17.(本题满分14分)请你为某养路处设计一个用于储藏食盐的仓库(供融化高速公路上的积雪之用).它的上部是底面圆半径为5m的圆锥,下部是底面圆半径为5m的圆柱,且该仓库的总高度为5m.经过预算,制造该仓库的圆锥侧面、圆柱侧面用料的单价分别为4百元/,1百元/,设圆锥母线与底面所成角为,且,问当为多少时,该仓库的侧面总造价(单位:百元)最少?并求出此时圆锥的高度.解:设该仓库的侧面总造价为y,则,(6分)由得,,所以,(10分)列表:所以当时,侧面总造价最小,此时圆锥的高度为m.(14分)18.(本题满分16分)定义:如果一个菱形的四个顶点均在一个椭圆上,那么该菱形叫做这个椭圆的内接菱形,且该0↘极小值↗6(第17题)菱形的对角线的交点为这个椭圆的中心.如图,在平面直角坐标系中,设椭圆的所有内接菱形构成的集合为.(1)求中菱形的最小的面积...